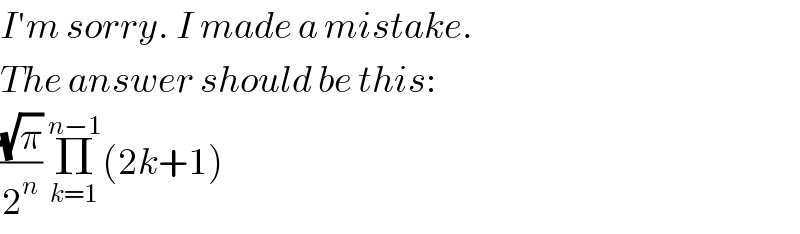Previous in Relation and Functions Next in Relation and Functions
Question Number 34719 by abdo mathsup 649 cc last updated on 10/May/18
$${calculate}\:\Gamma\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)\:{with}\:{n}\:\in{N}. \\ $$
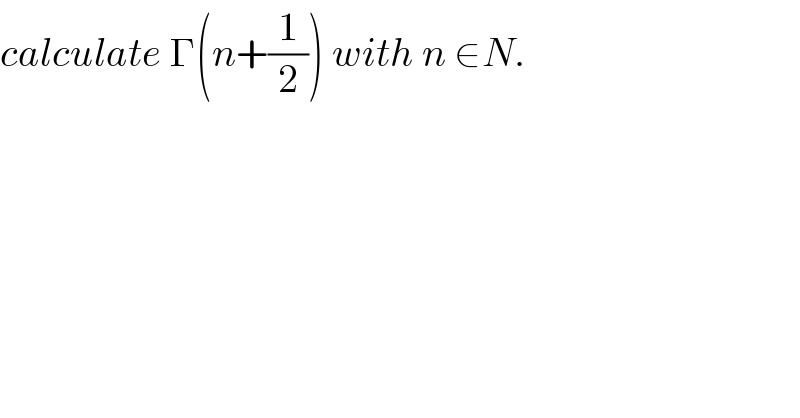
Commented by abdo mathsup 649 cc last updated on 12/May/18
![we have Γ(x)=∫_0 ^∞ t^(x−1) e^(−t) dt ⇒ Γ(n+(1/2)) = ∫_0 ^∞ t^(n−(1/2)) e^(−t) dt =_(t=u^2 ) ∫_0 ^∞ (u^2 )^(n−(1/2)) e^(−u^2 ) 2udu = 2∫_0 ^∞ u^(2n) e^(−u^2 ) du let put A_n = ∫_0 ^∞ u^(2n) e^(−u^2 ) du by parts α^′ =u^(2n) and β=e^(−u^2 ) A_n = [ (1/(2n+1)) u^(2n+1) e^(−u^2 ) ]_0 ^(+∞) − ∫_0 ^∞ (1/(2n+1)) u^(2n+1) (−2u)e^(−u^2 ) du = (2/(2n+1)) ∫_0 ^∞ u^(2n+2) e^(−u^2 ) du = (2/(2n+1)) A_(n+1) ⇒ A_(n+1) = ((2n+1)/2) A_n Π_(k=0) ^(n−1) A_(k+1) = ((Π_(k=0) ^(n−1) (2k+1))/2^n ) Π_(k=0) ^(n−1) A_n ⇒ A_n = ((Π_(k=0) ^(n−1) (2k+1))/2^n ) A_0 but A_0 =∫_0 ^∞ e^(−u^2 ) du =((√π)/2) ⇒ A_n = ((√π)/2^(n+1) ) ( 1.3.5....(2n−1)) = ((√π)/2^(n+1) ) ((1.2.3.4.....(2n))/(2^n n!)) =(((√π) (2n)!)/(2^(2n+1) (n!)))](Q34860.png)
$${we}\:{have}\:\Gamma\left({x}\right)=\int_{\mathrm{0}} ^{\infty} \:{t}^{{x}−\mathrm{1}} \:{e}^{−{t}} {dt}\:\Rightarrow \\ $$$$\Gamma\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)\:\:=\:\int_{\mathrm{0}} ^{\infty} \:{t}^{{n}−\frac{\mathrm{1}}{\mathrm{2}}} \:{e}^{−{t}} {dt}\: \\ $$$$=_{{t}={u}^{\mathrm{2}} } \:\:\:\int_{\mathrm{0}} ^{\infty} \:\:\:\left({u}^{\mathrm{2}} \right)^{{n}−\frac{\mathrm{1}}{\mathrm{2}}} \:{e}^{−{u}^{\mathrm{2}} } \:\mathrm{2}{udu} \\ $$$$=\:\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\:\:{u}^{\mathrm{2}{n}} \:\:{e}^{−{u}^{\mathrm{2}} } {du}\:\:{let}\:{put} \\ $$$${A}_{{n}} \:\:=\:\int_{\mathrm{0}} ^{\infty} {u}^{\mathrm{2}{n}} \:{e}^{−{u}^{\mathrm{2}} } {du}\:\:{by}\:{parts}\:\:\alpha^{'} \:={u}^{\mathrm{2}{n}} \:\:{and}\:\beta={e}^{−{u}^{\mathrm{2}} } \\ $$$${A}_{{n}} \:=\:\left[\:\:\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\:{u}^{\mathrm{2}{n}+\mathrm{1}} {e}^{−{u}^{\mathrm{2}} } \right]_{\mathrm{0}} ^{+\infty} \:\:−\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\:{u}^{\mathrm{2}{n}+\mathrm{1}} \:\left(−\mathrm{2}{u}\right){e}^{−{u}^{\mathrm{2}} } {du} \\ $$$$=\:\:\frac{\mathrm{2}}{\mathrm{2}{n}+\mathrm{1}}\:\int_{\mathrm{0}} ^{\infty} \:\:{u}^{\mathrm{2}{n}+\mathrm{2}} \:{e}^{−{u}^{\mathrm{2}} } {du}\:\:=\:\frac{\mathrm{2}}{\mathrm{2}{n}+\mathrm{1}}\:{A}_{{n}+\mathrm{1}} \\ $$$$\Rightarrow\:{A}_{{n}+\mathrm{1}} =\:\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{2}}\:{A}_{{n}} \: \\ $$$$\prod_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:{A}_{{k}+\mathrm{1}} \:=\:\frac{\prod_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \left(\mathrm{2}{k}+\mathrm{1}\right)}{\mathrm{2}^{{n}} }\:\prod_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:{A}_{{n}} \:\Rightarrow \\ $$$${A}_{{n}} \:\:=\:\frac{\prod_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\left(\mathrm{2}{k}+\mathrm{1}\right)}{\mathrm{2}^{{n}} }\:{A}_{\mathrm{0}} \:\:\:\:{but}\:{A}_{\mathrm{0}} =\int_{\mathrm{0}} ^{\infty} \:{e}^{−{u}^{\mathrm{2}} } {du}\:=\frac{\sqrt{\pi}}{\mathrm{2}} \\ $$$$\Rightarrow\:{A}_{{n}} \:\:=\:\frac{\sqrt{\pi}}{\mathrm{2}^{{n}+\mathrm{1}} }\:\:\left(\:\mathrm{1}.\mathrm{3}.\mathrm{5}....\left(\mathrm{2}{n}−\mathrm{1}\right)\right) \\ $$$$=\:\frac{\sqrt{\pi}}{\mathrm{2}^{{n}+\mathrm{1}} }\:\:\frac{\mathrm{1}.\mathrm{2}.\mathrm{3}.\mathrm{4}.....\left(\mathrm{2}{n}\right)}{\mathrm{2}^{{n}} {n}!}\:\:=\frac{\sqrt{\pi}\:\:\:\left(\mathrm{2}{n}\right)!}{\mathrm{2}^{\mathrm{2}{n}+\mathrm{1}} \:\left({n}!\right)} \\ $$
Commented by abdo mathsup 649 cc last updated on 12/May/18
$$\Gamma\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)\:=\mathrm{2}{A}_{{n}} \:\:\Rightarrow\:\Gamma\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)\:=\:\frac{\sqrt{\pi}}{\mathrm{2}^{\mathrm{2}{n}} }\:\:\frac{\left(\mathrm{2}{n}\right)!}{{n}!}\:. \\ $$
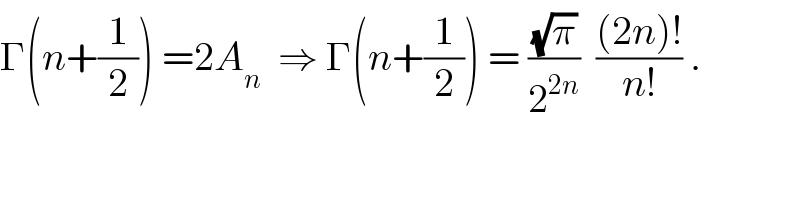
Answered by alex041103 last updated on 10/May/18
$${By}\:{definition}\:\Gamma\left({k}\right)=\left({k}−\mathrm{1}\right)!=\left({k}−\mathrm{1}\right)\left({k}−\mathrm{2}\right)!. \\ $$$${The}\:{value}\:\Gamma\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)=\left({n}−\frac{\mathrm{1}}{\mathrm{2}}\right)! \\ $$$$\Rightarrow\left({n}−\frac{\mathrm{1}}{\mathrm{2}}\right)!=\left({n}−\frac{\mathrm{1}}{\mathrm{2}}\right)\left({n}−\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)!=...= \\ $$$$=\left(\frac{\mathrm{1}}{\mathrm{2}}\right)!\underset{{k}=\mathrm{2}} {\overset{{n}} {\prod}}\frac{\mathrm{2}{k}−\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\pi}}{\mathrm{2}}\:\frac{\mathrm{1}}{\mathrm{2}^{{n}−\mathrm{1}} }\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\prod}}\left(\mathrm{2}{k}+\mathrm{1}\right) \\ $$$$\Rightarrow\Gamma\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\sqrt{\pi}}{\mathrm{2}^{{n}} }\:\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\prod}}\left(\mathrm{2}{k}+\mathrm{1}\right) \\ $$
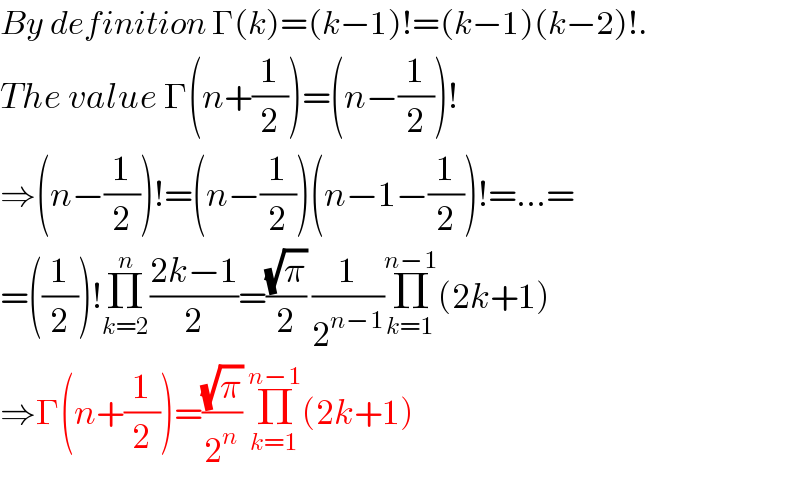
Commented by NECx last updated on 10/May/18
$${welcome}\:{back}\:{mr}\:{Alex} \\ $$
Commented by alex041103 last updated on 10/May/18
$${I}'{m}\:{sorry}.\:{I}\:{made}\:{a}\:{mistake}. \\ $$$${The}\:{answer}\:{should}\:{be}\:{this}: \\ $$$$\frac{\sqrt{\pi}}{\mathrm{2}^{{n}} }\:\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\prod}}\left(\mathrm{2}{k}+\mathrm{1}\right) \\ $$