Question Number 34821 by ajfour last updated on 11/May/18
$${Find}\:{range}\:{of} \\ $$$$\:\:\:{y}=\frac{{x}}{\left({x}−\mathrm{1}\right)\left({x}−\mathrm{2}\right)}\:. \\ $$
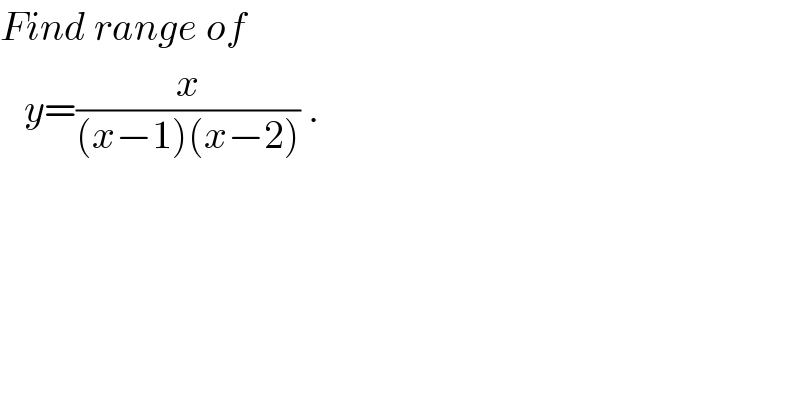
Commented by ajfour last updated on 11/May/18
Answered by ajfour last updated on 11/May/18
![(dy/dx)=((x^2 −3x+2−x(2x−3))/((x−1)^2 (x−2)^2 )) (dy/dx)=0 ⇒ x^2 =2 ⇒ x=±(√2) y∣_(x=−(√2)) =b=((−(√2))/((−(√2)−1)(−(√2)−2))) ⇒ b=−(1/(((√2)+1)^2 )) = −(1/((3+2(√2)))) =−(3−2(√2)) y∣_(x=(√2)) =a =((√2)/(((√2)−1)((√2)−2))) ⇒ a=−(1/(((√2)−1)^2 )) a=−(1/(3−2(√2))) = −(3+2(√2)) So, y∈ (−∞, −3−2(√2)] ∪ [2(√2)−3,∞) .](Q34847.png)
$$\frac{{dy}}{{dx}}=\frac{{x}^{\mathrm{2}} −\mathrm{3}{x}+\mathrm{2}−{x}\left(\mathrm{2}{x}−\mathrm{3}\right)}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} \left({x}−\mathrm{2}\right)^{\mathrm{2}} } \\ $$$$\frac{{dy}}{{dx}}=\mathrm{0}\:\:\Rightarrow\:\:\:{x}^{\mathrm{2}} =\mathrm{2}\:\:\:\Rightarrow\:\:\:{x}=\pm\sqrt{\mathrm{2}} \\ $$$${y}\mid_{{x}=−\sqrt{\mathrm{2}}} \:={b}=\frac{−\sqrt{\mathrm{2}}}{\left(−\sqrt{\mathrm{2}}−\mathrm{1}\right)\left(−\sqrt{\mathrm{2}}−\mathrm{2}\right)} \\ $$$$\:\:\:\:\:\Rightarrow\:\:\:\:{b}=−\frac{\mathrm{1}}{\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)^{\mathrm{2}} }\:=\:−\frac{\mathrm{1}}{\left(\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\right)} \\ $$$$\:\:\:\:\:\:\:\:=−\left(\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}\right) \\ $$$${y}\mid_{{x}=\sqrt{\mathrm{2}}} \:={a}\:=\frac{\sqrt{\mathrm{2}}}{\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\left(\sqrt{\mathrm{2}}−\mathrm{2}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\:\:{a}=−\frac{\mathrm{1}}{\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:{a}=−\frac{\mathrm{1}}{\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}}\:=\:−\left(\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\right) \\ $$$${So}, \\ $$$${y}\in\:\left(−\infty,\:−\mathrm{3}−\mathrm{2}\sqrt{\mathrm{2}}\right]\:\cup\:\left[\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{3},\infty\right)\:. \\ $$
Commented by NECx last updated on 12/May/18
$${wow}....\:{This}\:{style}\:{is}\:{new}\:{to}\:{me}. \\ $$$${Thanks} \\ $$
Answered by Joel579 last updated on 11/May/18
$${y}\left({x}^{\mathrm{2}} \:−\:\mathrm{3}{x}\:+\:\mathrm{2}\right)\:=\:{x} \\ $$$${yx}^{\mathrm{2}} \:−\:\mathrm{3}{yx}\:−\:{x}\:+\:\mathrm{2}{y}\:=\:\mathrm{0} \\ $$$${yx}^{\mathrm{2}} \:−\:\left(\mathrm{3}{y}\:+\:\mathrm{1}\right){x}\:+\:\mathrm{2}{y}\:=\:\mathrm{0} \\ $$$${x}\:=\:\frac{\left(\mathrm{3}{y}\:+\:\mathrm{1}\right)\:\pm\:\sqrt{\left(\mathrm{3}{y}\:+\:\mathrm{1}\right)^{\mathrm{2}} \:−\:\mathrm{4}{y}\left(\mathrm{2}{y}\right)}}{\mathrm{2}{y}} \\ $$$$\:\:\:\:=\:\frac{\left(\mathrm{3}{y}\:+\:\mathrm{1}\right)\:\pm\:\sqrt{{y}^{\mathrm{2}} \:+\:\mathrm{6}{y}\:+\:\mathrm{1}}}{\mathrm{2}{y}} \\ $$$${y}\:\neq\:\mathrm{0} \\ $$$${y}^{\mathrm{2}} \:+\:\mathrm{6}{y}\:+\:\mathrm{1}\:\geqslant\:\mathrm{0} \\ $$$${y}\:\leqslant\:−\mathrm{3}\:−\:\mathrm{2}\sqrt{\mathrm{2}}\:\:\:\vee\:\:{y}\:\geqslant\:−\mathrm{3}\:+\:\mathrm{2}\sqrt{\mathrm{2}} \\ $$