Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 35059 by math khazana by abdo last updated on 14/May/18

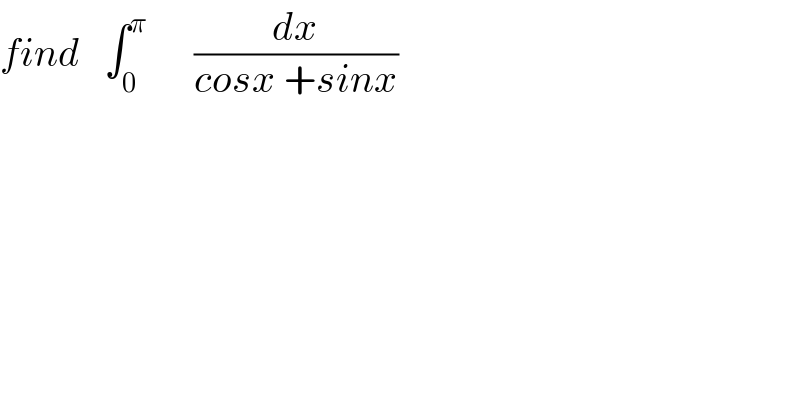
find ∫_0 ^π (dx/(cosx +sinx))

$${find}\:\:\:\int_{\mathrm{0}} ^{\pi} \:\:\:\:\:\:\frac{{dx}}{{cosx}\:+{sinx}} \\ $$

Commented by math khazana by abdo last updated on 15/May/18

let put I = ∫_0 ^π (dx/(cosx +sinx)) changement tan((x/2))=t give x=2arctant and I = ∫_0 ^(+∞) (1/(((1−t^2 )/(1+t^2 )) +((2t)/(1+t^2 )))) ((2dt)/(1+t^2 )) I = ∫_0 ^(+∞) ((2dt)/(1−t^2 +2t)) = −2 ∫_0 ^∞ (dt/(t^2 −2t −1)) =−2 ∫_0 ^∞ (dt/((t−1)^2 −2)) =−2 ∫_0 ^∞ (dt/((t−3)(t+1))) =(1/2) ∫_0 ^∞ { (1/(t+1)) −(1/(t−3))}dt =(1/2) [ln∣((t+1)/(t−3))∣]_0 ^(+∞) =(1/2)( −ln((1/3))) I =(1/2)ln(3).

$${let}\:{put}\:{I}\:=\:\int_{\mathrm{0}} ^{\pi} \:\:\:\:\frac{{dx}}{{cosx}\:+{sinx}}\:\:{changement} \\ $$$${tan}\left(\frac{{x}}{\mathrm{2}}\right)={t}\:{give}\:\:{x}=\mathrm{2}{arctant}\:{and} \\ $$$${I}\:=\:\int_{\mathrm{0}} ^{+\infty} \:\:\:\:\:\frac{\mathrm{1}}{\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\:+\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }}\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$${I}\:=\:\int_{\mathrm{0}} ^{+\infty} \:\:\:\:\:\:\:\frac{\mathrm{2}{dt}}{\mathrm{1}−{t}^{\mathrm{2}} \:+\mathrm{2}{t}}\:=\:−\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{{dt}}{{t}^{\mathrm{2}} \:−\mathrm{2}{t}\:−\mathrm{1}} \\ $$$$=−\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\:\frac{{dt}}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} \:−\mathrm{2}} \\ $$$$=−\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\:\frac{{dt}}{\left({t}−\mathrm{3}\right)\left({t}+\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\infty} \left\{\:\frac{\mathrm{1}}{{t}+\mathrm{1}}\:−\frac{\mathrm{1}}{{t}−\mathrm{3}}\right\}{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\left[{ln}\mid\frac{{t}+\mathrm{1}}{{t}−\mathrm{3}}\mid\right]_{\mathrm{0}} ^{+\infty} \:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left(\:−{ln}\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\right) \\ $$$${I}\:=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{3}\right). \\ $$

Commented by prof Abdo imad last updated on 16/May/18

error in the final lines I =−2 ∫_0 ^∞ (dt/((t−1)^2 −2)) =−2 ∫_0 ^∞ (dt/((t−1−_ (√2))(t−1 +(√2)))) =((−2)/(2(√2)))∫_0 ^∞ { (1/(t−1−(√2))) −(1/(t−1+(√2)))}dt =−(1/(√2))[ln∣((t−1−(√2))/(t−1+(√2)))]]_0 ^(+∞) =((−1)/(√2))( −ln(((1+(√2))/((√2) −1)))) I = (1/(√2))ln(((1+(√2))/(−1+(√2))))

$${error}\:{in}\:{the}\:{final}\:{lines} \\ $$$${I}\:=−\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{dt}}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}} \\ $$$$=−\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\:\frac{{dt}}{\left({t}−\mathrm{1}−_{} \sqrt{\mathrm{2}}\right)\left({t}−\mathrm{1}\:+\sqrt{\mathrm{2}}\right)} \\ $$$$=\frac{−\mathrm{2}}{\mathrm{2}\sqrt{\mathrm{2}}}\int_{\mathrm{0}} ^{\infty} \:\:\:\:\left\{\:\:\frac{\mathrm{1}}{{t}−\mathrm{1}−\sqrt{\mathrm{2}}}\:−\frac{\mathrm{1}}{{t}−\mathrm{1}+\sqrt{\mathrm{2}}}\right\}{dt} \\ $$$$\left.=−\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\left[{ln}\mid\frac{{t}−\mathrm{1}−\sqrt{\mathrm{2}}}{{t}−\mathrm{1}+\sqrt{\mathrm{2}}}\right]\right]_{\mathrm{0}} ^{+\infty} \\ $$$$=\frac{−\mathrm{1}}{\sqrt{\mathrm{2}}}\left(\:−{ln}\left(\frac{\mathrm{1}+\sqrt{\mathrm{2}}}{\sqrt{\mathrm{2}}\:−\mathrm{1}}\right)\right)\: \\ $$$${I}\:=\:\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}{ln}\left(\frac{\mathrm{1}+\sqrt{\mathrm{2}}}{−\mathrm{1}+\sqrt{\mathrm{2}}}\right) \\ $$$$ \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 15/May/18

I=∫_0 ^Π (dx/(cos(Π−x)+sin(Π−x))) 2I=∫_0 ^Π (1/(cosx+sinx))+(1/(−cosx+sinx)) dx =∫_0 ^Π ((2sinx)/(sin^2 x−cos^2 x)) dx I=(1/2)∫_0 ^Π ((2sinx)/(1−2cos^2 x))dx =∫_0 ^Π (((−sinx))/(2cos^2 x−1))dx =(1/2)∫_0 ^Π ((d(cosx))/(cos^2 x−((1/(√2)))^2 )) =(1/2)×((√2)/2)∣ln((cosx−(1/(√2)))/(cosx+(1/(√2))))∣_0 ^Π

$${I}=\int_{\mathrm{0}} ^{\Pi} \frac{{dx}}{{cos}\left(\Pi−{x}\right)+{sin}\left(\Pi−{x}\right)} \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\Pi} \frac{\mathrm{1}}{{cosx}+{sinx}}+\frac{\mathrm{1}}{−{cosx}+{sinx}}\:{dx} \\ $$$$=\int_{\mathrm{0}} ^{\Pi} \frac{\mathrm{2}{sinx}}{{sin}^{\mathrm{2}} {x}−{cos}^{\mathrm{2}} {x}}\:{dx} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\Pi} \frac{\mathrm{2}{sinx}}{\mathrm{1}−\mathrm{2}{cos}^{\mathrm{2}} {x}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\Pi} \frac{\left(−{sinx}\right)}{\mathrm{2}{cos}^{\mathrm{2}} {x}−\mathrm{1}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\Pi} \frac{{d}\left({cosx}\right)}{{cos}^{\mathrm{2}} {x}−\left(\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mid{ln}\frac{{cosx}−\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}}{{cosx}+\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}}\mid_{\mathrm{0}} ^{\Pi} \\ $$

Commented by NECx last updated on 15/May/18

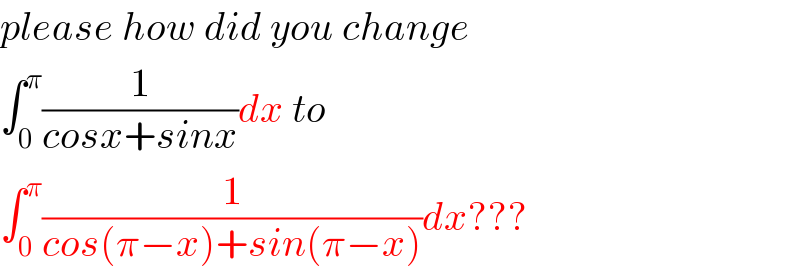
please how did you change ∫_0 ^π (1/(cosx+sinx))dx to ∫_0 ^π (1/(cos(π−x)+sin(π−x)))dx???

$${please}\:{how}\:{did}\:{you}\:{change} \\ $$$$\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{1}}{{cosx}+{sinx}}{dx}\:{to} \\ $$$$\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{1}}{{cos}\left(\pi−{x}\right)+{sin}\left(\pi−{x}\right)}{dx}??? \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 15/May/18

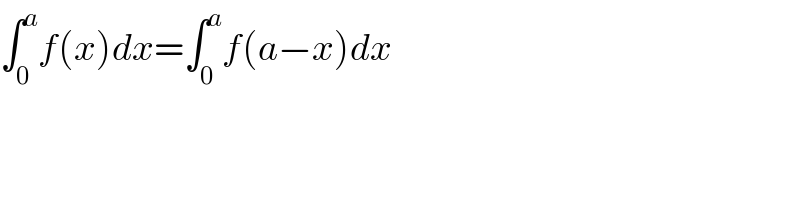
∫_0 ^a f(x)dx=∫_0 ^a f(a−x)dx

$$\int_{\mathrm{0}} ^{{a}} {f}\left({x}\right){dx}=\int_{\mathrm{0}} ^{{a}} {f}\left({a}−{x}\right){dx} \\ $$

Commented by NECx last updated on 15/May/18

oh... Thanks

$${oh}...\:{Thanks} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 15/May/18

∫(dx/(cosx+sinx)) t=tan(x/2) dt=(1/2)sec^2 (x/2) ∫(dx/(((1−tan^2 (x/2))/(1+tan^2 (x/2)))+((2tan(x/2))/(1+tan^2 (x/2))))) ∫((sec^2 (x/2))/(1−tan^2 (x/2)+2tan(x/2))) ∫((2dt)/(1−t^2 +2t)) −2∫(dt/(t^2 −2t+1−2)) −2∫(dt/((t−1)^2 −((√2))^2 )) now use formula and put limit or method ∫_0 ^Π (dx/(cosx+sinx)) =∫_0 ^Π (((1/(√2))dx)/((1/(√2))cosx+(1/(√2))sinx)) =(1/(√2))∫_0 ^Π (dx/(sin(Π/4+x))) now useformula and put limit

$$\int\frac{{dx}}{{cosx}+{sinx}} \\ $$$${t}={tan}\frac{{x}}{\mathrm{2}}\:\:{dt}=\frac{\mathrm{1}}{\mathrm{2}}{sec}^{\mathrm{2}} \frac{{x}}{\mathrm{2}} \\ $$$$\int\frac{{dx}}{\frac{\mathrm{1}−{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{\mathrm{1}+{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}+\frac{\mathrm{2}{tan}\frac{{x}}{\mathrm{2}}}{\mathrm{1}+{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}} \\ $$$$\int\frac{{sec}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{\mathrm{1}−{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}+\mathrm{2}{tan}\frac{{x}}{\mathrm{2}}} \\ $$$$\int\frac{\mathrm{2}{dt}}{\mathrm{1}−{t}^{\mathrm{2}} +\mathrm{2}{t}} \\ $$$$−\mathrm{2}\int\frac{{dt}}{{t}^{\mathrm{2}} −\mathrm{2}{t}+\mathrm{1}−\mathrm{2}} \\ $$$$−\mathrm{2}\int\frac{{dt}}{\left({t}−\mathrm{1}\right)^{\mathrm{2}} −\left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$${now}\:{use}\:{formula}\:{and}\:{put}\:{limit} \\ $$$$ \\ $$$${or}\:{method} \\ $$$$\int_{\mathrm{0}} ^{\Pi} \frac{{dx}}{{cosx}+{sinx}} \\ $$$$=\int_{\mathrm{0}} ^{\Pi} \frac{\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}{dx}}{\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}{cosx}+\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}{sinx}} \\ $$$$=\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\int_{\mathrm{0}} ^{\Pi} \frac{{dx}}{{sin}\left(\Pi/\mathrm{4}+{x}\right)} \\ $$$$ \\ $$$$ \\ $$$${now}\:{useformula}\:{and}\:{put}\:{limit} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com