Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 35229 by abdo mathsup 649 cc last updated on 16/May/18

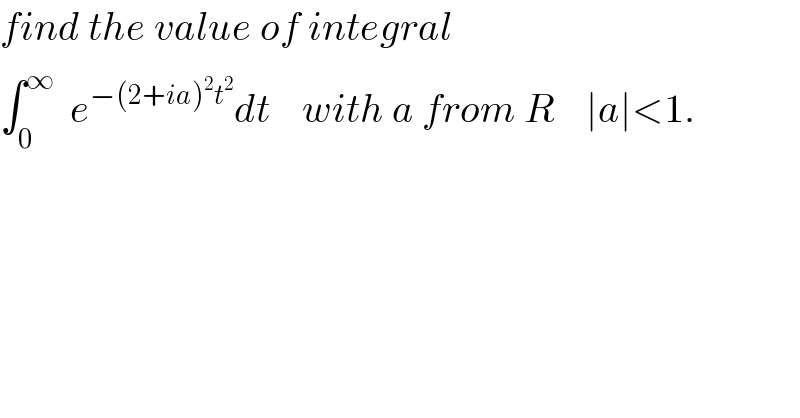
find the value of integral ∫_0 ^∞ e^(−(2+ia)^2 t^2 ) dt with a from R ∣a∣<1.

$${find}\:{the}\:{value}\:{of}\:{integral} \\ $$ $$\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−\left(\mathrm{2}+{ia}\right)^{\mathrm{2}} {t}^{\mathrm{2}} } {dt}\:\:\:\:{with}\:{a}\:{from}\:{R}\:\:\:\:\mid{a}\mid<\mathrm{1}. \\ $$

Commented byabdo mathsup 649 cc last updated on 17/May/18

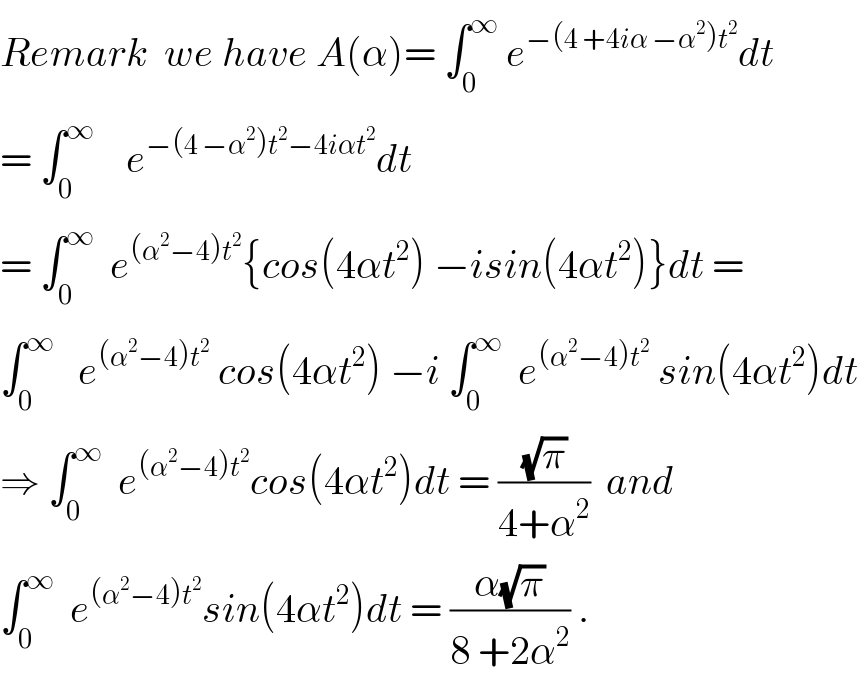
Remark we have A(α)= ∫_0 ^∞ e^(−(4 +4iα −α^2 )t^2 ) dt = ∫_0 ^∞ e^(−(4 −α^2 )t^2 −4iαt^2 ) dt = ∫_0 ^∞ e^((α^2 −4)t^2 ) {cos(4αt^2 ) −isin(4αt^2 )}dt = ∫_0 ^∞ e^((α^2 −4)t^2 ) cos(4αt^2 ) −i ∫_0 ^∞ e^((α^2 −4)t^2 ) sin(4αt^2 )dt ⇒ ∫_0 ^∞ e^((α^2 −4)t^2 ) cos(4αt^2 )dt = ((√π)/(4+α^2 )) and ∫_0 ^∞ e^((α^2 −4)t^2 ) sin(4αt^2 )dt = ((α(√π))/(8 +2α^2 )) .

$${Remark}\:\:{we}\:{have}\:{A}\left(\alpha\right)=\:\int_{\mathrm{0}} ^{\infty} \:{e}^{−\left(\mathrm{4}\:+\mathrm{4}{i}\alpha\:−\alpha^{\mathrm{2}} \right){t}^{\mathrm{2}} } {dt} \\ $$ $$=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:{e}^{−\left(\mathrm{4}\:−\alpha^{\mathrm{2}} \right){t}^{\mathrm{2}} −\mathrm{4}{i}\alpha{t}^{\mathrm{2}} } {dt} \\ $$ $$=\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{\left(\alpha^{\mathrm{2}} −\mathrm{4}\right){t}^{\mathrm{2}} } \left\{{cos}\left(\mathrm{4}\alpha{t}^{\mathrm{2}} \right)\:−{isin}\left(\mathrm{4}\alpha{t}^{\mathrm{2}} \right)\right\}{dt}\:= \\ $$ $$\int_{\mathrm{0}} ^{\infty} \:\:\:{e}^{\left(\alpha^{\mathrm{2}} −\mathrm{4}\right){t}^{\mathrm{2}} } \:{cos}\left(\mathrm{4}\alpha{t}^{\mathrm{2}} \right)\:−{i}\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{\left(\alpha^{\mathrm{2}} −\mathrm{4}\right){t}^{\mathrm{2}} } \:{sin}\left(\mathrm{4}\alpha{t}^{\mathrm{2}} \right){dt} \\ $$ $$\Rightarrow\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{\left(\alpha^{\mathrm{2}} −\mathrm{4}\right){t}^{\mathrm{2}} } {cos}\left(\mathrm{4}\alpha{t}^{\mathrm{2}} \right){dt}\:=\:\frac{\sqrt{\pi}}{\mathrm{4}+\alpha^{\mathrm{2}} }\:\:{and} \\ $$ $$\int_{\mathrm{0}} ^{\infty} \:\:{e}^{\left(\alpha^{\mathrm{2}} −\mathrm{4}\right){t}^{\mathrm{2}} } {sin}\left(\mathrm{4}\alpha{t}^{\mathrm{2}} \right){dt}\:=\:\frac{\alpha\sqrt{\pi}}{\mathrm{8}\:+\mathrm{2}\alpha^{\mathrm{2}} }\:. \\ $$

Commented byabdo mathsup 649 cc last updated on 17/May/18

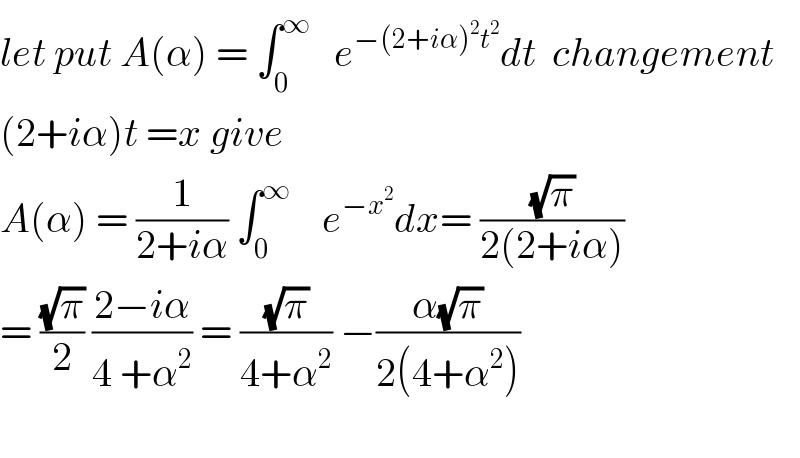
let put A(α) = ∫_0 ^∞ e^(−(2+iα)^2 t^2 ) dt changement (2+iα)t =x give A(α) = (1/(2+iα)) ∫_0 ^∞ e^(−x^2 ) dx= ((√π)/(2(2+iα))) = ((√π)/2) ((2−iα)/(4 +α^2 )) = ((√π)/(4+α^2 )) −((α(√π))/(2(4+α^2 )))

$${let}\:{put}\:{A}\left(\alpha\right)\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:{e}^{−\left(\mathrm{2}+{i}\alpha\right)^{\mathrm{2}} {t}^{\mathrm{2}} } {dt}\:\:{changement} \\ $$ $$\left(\mathrm{2}+{i}\alpha\right){t}\:={x}\:{give} \\ $$ $${A}\left(\alpha\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}+{i}\alpha}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:{e}^{−{x}^{\mathrm{2}} } {dx}=\:\frac{\sqrt{\pi}}{\mathrm{2}\left(\mathrm{2}+{i}\alpha\right)} \\ $$ $$=\:\frac{\sqrt{\pi}}{\mathrm{2}}\:\frac{\mathrm{2}−{i}\alpha}{\mathrm{4}\:+\alpha^{\mathrm{2}} }\:=\:\frac{\sqrt{\pi}}{\mathrm{4}+\alpha^{\mathrm{2}} }\:−\frac{\alpha\sqrt{\pi}}{\mathrm{2}\left(\mathrm{4}+\alpha^{\mathrm{2}} \right)} \\ $$ $$ \\ $$

Answered by sma3l2996 last updated on 16/May/18

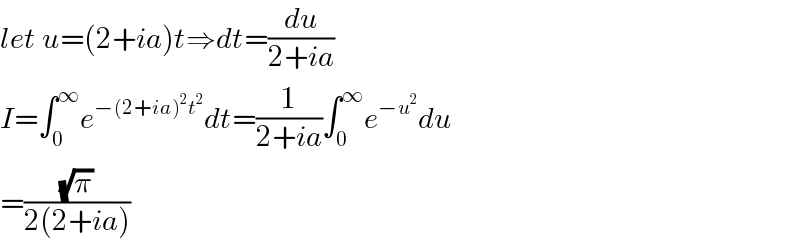
let u=(2+ia)t⇒dt=(du/(2+ia)) I=∫_0 ^∞ e^(−(2+ia)^2 t^2 ) dt=(1/(2+ia))∫_0 ^∞ e^(−u^2 ) du =((√π)/(2(2+ia)))

$${let}\:{u}=\left(\mathrm{2}+{ia}\right){t}\Rightarrow{dt}=\frac{{du}}{\mathrm{2}+{ia}} \\ $$ $${I}=\int_{\mathrm{0}} ^{\infty} {e}^{−\left(\mathrm{2}+{ia}\right)^{\mathrm{2}} {t}^{\mathrm{2}} } {dt}=\frac{\mathrm{1}}{\mathrm{2}+{ia}}\int_{\mathrm{0}} ^{\infty} {e}^{−{u}^{\mathrm{2}} } {du} \\ $$ $$=\frac{\sqrt{\pi}}{\mathrm{2}\left(\mathrm{2}+{ia}\right)} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com