calculate ∫_0 ^π ((x dx)/(3 +cosx)) .


Question and Answers Forum

All Questions Topic List
Integration Questions
Previous in All Question Next in All Question
Previous in Integration Next in Integration
Question Number 35241 by abdo mathsup 649 cc last updated on 17/May/18

$c a l c u l a t e \int_{0}^{π} \frac{x d x}{3 + c o s x} .$
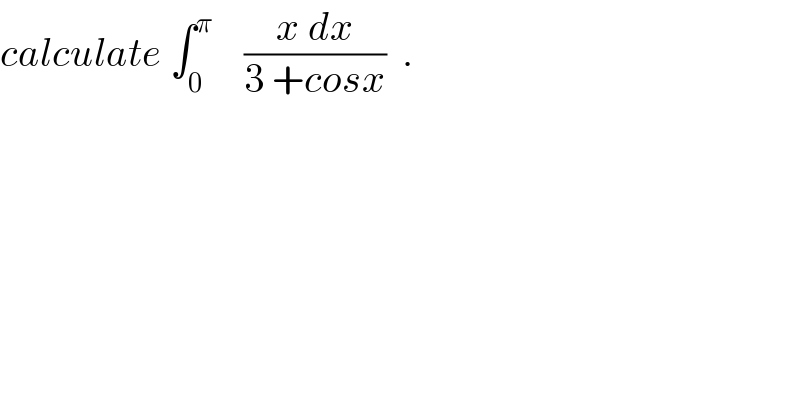
Commented by abdo.msup.com last updated on 17/May/18
$let put I=∫_0 ^π ((xdx)/(3 +cosx)) .changement tan((x/2))=t give x =2arctan(t) and I = ∫_0 ^∞ ((2arctan(t))/(3 +((1−t^2 )/(2+t^2 )))) ((2dt)/(1+t^2 )) = 4∫_0 ^∞ ((arctan(t))/(3 +3t^2 +1−t^2 ))dt =4 ∫_0 ^∞ ((arctan(t))/(4 +2t^2 ))dt=2∫_0 ^∞ ((arctan(t))/(2 +t^2 )) =_(t=x(√2)) 2∫_0 ^∞ ((arctan(x(√2)))/(2(1+x^2 )))(√2) dx =(√2) ∫_0 ^∞ ((arctan(x(√2)))/(1+x^2 ))dx let introduce the parametric function f(t) =∫_0 ^∞ ((arctan(tx))/(1+x^2 ))dx f^′ (t) = ∫_0 ^∞ (x/((1+t^2 x^2 )(1+x^2 )))dx =_(tx =u) ∫_0 ^∞ (u/(t(1+u^2 )(1+(u^2 /t^2 )))) (du/t) = ∫_0 ^∞ (u/((1+u^2 )(t^2 +u^2 )))du let decompose g(u)= (u/((u^2 +1)(u^2 +t^2 ))) g(u) = ((au +b)/(u^2 +1)) +((cu +d)/(u^2 +t^2 )) g(−u) =−g(u) ⇒b=d=0 so g(u)= ((au)/(u^2 +1)) +((cu)/(u^2 +t^2 )) lim_(u→+∞) u g(u)=0 = a+c ⇒c=−a g(u)= ((au)/(u^2 +1)) −((au)/(u^2 +t^2 )) g(1)=(1/(2(1+t^2 ))) = (a/2) −(a/(t^2 +1)) ⇒ (1/2) =(1/2)(1+t^2 )a −a ⇒ 1=(1+t^2 )a −2a =(t^2 −1)a ⇒ a= (1/(t^2 −1)) if t^2 ≠1 so g(u) = (1/(t^2 −1)) (u/(1+u^2 )) −(1/(t^2 −1)) (u/(t^2 +u^2 )) f^′ (t) =∫_0 ^∞ g(u)du =(1/(1−t^2 )){ ∫_0 ^∞ (u/(1+u^2 ))du −∫_0 ^∞ (u/(u^2 +t^2 ))du} = (1/(2(1−t^2 )))[ ln(1+u^2 )−ln(u^2 +t^2 )]_0 ^(+∞) = (1/(2(1−t^2 )))[ln(((u^2 +1)/(u^2 +t^2 )))]_0 ^(+∞) = (1/(2(1−t^2 ))) {ln(t^2 )= ((ln(t))/(1−t^2 )) f^′ (t) = ((ln(t))/(1−t^2 )) ⇒f(t)= ∫_0 ^t ((lnx)/(1−x^2 ))dx +λ λ=f(0)=0 ⇒ f(t)= ∫_0 ^t ((ln(x))/(1−x^2 ))dx I =(√2) f((√2))= (√2) ∫_0 ^(√2) ((ln(x))/(1−x^2 ))dx... be continued...$
$l e t p u t I = \int_{0}^{π} \frac{x d x}{3 + c o s x} . c h a n g e m e n t$ $t a n (\frac{x}{2}) = t g i v e x = 2 a r c t a n (t) a n d$ $I = \int_{0}^{\infty} \frac{2 a r c t a n (t)}{3 + \frac{1 - t^{2}}{2 + t^{2}}} \frac{2 d t}{1 + t^{2}}$ $= 4 \int_{0}^{\infty} \frac{a r c t a n (t)}{3 + 3 t^{2} + 1 - t^{2}} d t$ $= 4 \int_{0}^{\infty} \frac{a r c t a n (t)}{4 + 2 t^{2}} d t = 2 \int_{0}^{\infty} \frac{a r c t a n (t)}{2 + t^{2}}$ $=_{t = x \sqrt{2}} 2 \int_{0}^{\infty} \frac{a r c t a n (x \sqrt{2})}{2 (1 + x^{2})} \sqrt{2} d x$ $= \sqrt{2} \int_{0}^{\infty} \frac{a r c t a n (x \sqrt{2})}{1 + x^{2}} d x l e t i n t r o d u c e$ $t h e p a r a m e t r i c f u n c t i o n$ $f (t) = \int_{0}^{\infty} \frac{a r c t a n (t x)}{1 + x^{2}} d x$ $f^{^{'}} (t) = \int_{0}^{\infty} \frac{x}{(1 + t^{2} x^{2}) (1 + x^{2})} d x$ $=_{t x = u} \int_{0}^{\infty} \frac{u}{t (1 + u^{2}) (1 + \frac{u^{2}}{t^{2}})} \frac{d u}{t}$ $= \int_{0}^{\infty} \frac{u}{(1 + u^{2}) (t^{2} + u^{2})} d u l e t$ $d e c o m p o s e g (u) = \frac{u}{(u^{2} + 1) (u^{2} + t^{2})}$ $g (u) = \frac{a u + b}{u^{2} + 1} + \frac{c u + d}{u^{2} + t^{2}}$ $g (- u) = - g (u) \Rightarrow b = d = 0 s o$ $g (u) = \frac{a u}{u^{2} + 1} + \frac{c u}{u^{2} + t^{2}}$ ${l i m}_{u \to + \infty} u g (u) = 0 = a + c \Rightarrow c = - a$ $g (u) = \frac{a u}{u^{2} + 1} - \frac{a u}{u^{2} + t^{2}}$ $g (1) = \frac{1}{2 (1 + t^{2})} = \frac{a}{2} - \frac{a}{t^{2} + 1} \Rightarrow$ $\frac{1}{2} = \frac{1}{2} (1 + t^{2}) a - a \Rightarrow$ $1 = (1 + t^{2}) a - 2 a = (t^{2} - 1) a \Rightarrow$ $a = \frac{1}{t^{2} - 1} i f t^{2} \neq 1 s o$ $g (u) = \frac{1}{t^{2} - 1} \frac{u}{1 + u^{2}} - \frac{1}{t^{2} - 1} \frac{u}{t^{2} + u^{2}}$ $f^{^{'}} (t) = \int_{0}^{\infty} g (u) d u$ $= \frac{1}{1 - t^{2}} {\int_{0}^{\infty} \frac{u}{1 + u^{2}} d u - \int_{0}^{\infty} \frac{u}{u^{2} + t^{2}} d u}$ $= \frac{1}{2 (1 - t^{2})} {[l n (1 + u^{2}) - l n (u^{2} + t^{2})]}_{0}^{+ \infty}$ $= \frac{1}{2 (1 - t^{2})} {[l n (\frac{u^{2} + 1}{u^{2} + t^{2}})]}_{0}^{+ \infty}$ $= \frac{1}{2 (1 - t^{2})} {l n (t^{2}) = \frac{l n (t)}{1 - t^{2}}$ $f^{^{'}} (t) = \frac{l n (t)}{1 - t^{2}} \Rightarrow f (t) = \int_{0}^{t} \frac{l n x}{1 - x^{2}} d x + λ$ $λ = f (0) = 0 \Rightarrow f (t) = \int_{0}^{t} \frac{l n (x)}{1 - x^{2}} d x$ $I = \sqrt{2} f (\sqrt{2}) = \sqrt{2} \int_{0}^{\sqrt{2}} \frac{l n (x)}{1 - x^{2}} d x . . .$ $b e c o n t i n u e d . . .$
Commented by abdo.msup.com last updated on 17/May/18

$e r r o r c h a n g e 1 - t^{2} b y t^{2} - 1 s o$ $f (t) = \int_{0}^{t} \frac{l n (x)}{x^{2} - 1} d x$ $I = \sqrt{2} \int_{0}^{\sqrt{2}} \frac{l n (x)}{x^{2} - 1} d x .$
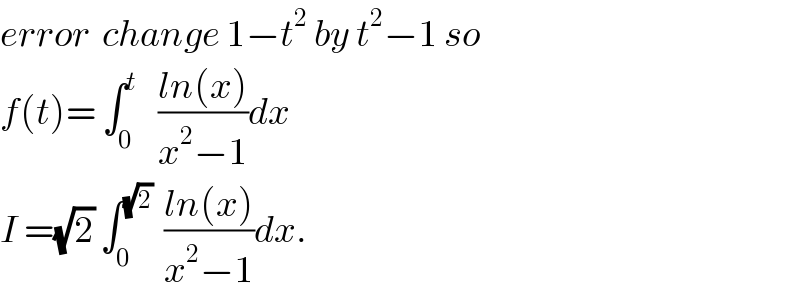
Commented by abdo mathsup 649 cc last updated on 20/May/18

$\int_{0}^{\sqrt{2}} \frac{l n x}{x^{2} - 1} d x = - \int_{0}^{1} \frac{l n x}{1 - x^{2}} d x + \int_{1}^{\sqrt{2}} \frac{l n x}{x^{2} - 1} d x b u t$ $\int_{0}^{1} \frac{l n (x)}{1 - x^{2}} d x = \int_{0}^{1} (\sum_{n = 0}^{\infty} x^{2 n}) l n x d x$ $= \sum_{n = 0}^{\infty} \int_{0}^{1} x^{2 n} l n (x) d x b y p a r t s$ $A_{n} = \int_{0}^{1} x^{2 n} l n (x) d x = {[\frac{1}{2 n + 1} x^{2 n + 1} l n (x)]}_{0}^{1}$ $- \int_{0}^{1} \frac{1}{2 n + 1} x^{2 n + 1} \frac{1}{x} d x = - \frac{1}{{(2 n + 1)}^{2}} \int_{0}^{1} x^{2 n} d x$ $= - \frac{1}{{(2 n + 1)}^{2}} \Rightarrow \int_{0}^{1} \frac{l n (x)}{1 - x^{2}} d x = - \sum_{n = 0}^{\infty} \frac{1}{{(2 n + 1)}^{2}}$ $w e h a v e \frac{π^{2}}{6} = \sum_{n = 1}^{\infty} \frac{1}{n^{2}} = \sum_{n = 1}^{\infty} \frac{1}{{(2 n)}^{2}} + \sum_{n = 0}^{\infty} \frac{1}{{(2 n + 1)}^{2}}$ $= \frac{1}{4} \sum_{n = 1}^{\infty} \frac{1}{n^{2}} + \sum_{n = 0}^{\infty} \frac{1}{{(2 n + 1)}^{2}} \Rightarrow$ $\sum_{n = 0}^{\infty} \frac{1}{{(2 n + 1)}^{2}} = \frac{3}{4} \sum_{n = 1}^{\infty} \frac{1}{n^{2}} = \frac{3}{4} \frac{π^{2}}{6} = \frac{π^{2}}{8}$
Commented by abdo mathsup 649 cc last updated on 20/May/18

$\Rightarrow \int_{0}^{1} \frac{l n (x)}{x^{2} - 1} d x = - \frac{π^{2}}{8}$ $c h a n g e m e n t x = \frac{1}{t} g i v e$ $\int_{1}^{\sqrt{2}} \frac{l n (x)}{x^{2} - 1} d x = \int_{1}^{\frac{1}{\sqrt{2}}} \frac{- l n (t)}{(\frac{1}{t^{2}} - 1)} (- \frac{d t}{t^{2}})$ $= - \int_{\frac{1}{\sqrt{2}}}^{1} \frac{l n (t)}{1 - t^{2}} d t = - \int_{\frac{1}{\sqrt{2}}}^{1} (\sum_{n = 0}^{\infty} t^{2 n}) l n (t) d t$ $= - \sum_{n = 0}^{\infty} \int_{\frac{1}{\sqrt{2}}}^{1} t^{2 n} l n (t) d t = - \sum_{n = 0}^{\infty} A_{n} b y p a r t s$ $A_{n} = {[\frac{1}{2 n + 1} t^{2 n + 1} l n (t)]}_{\frac{1}{\sqrt{2}}}^{1} - \int_{\frac{1}{\sqrt{2}}}^{1} \frac{1}{2 n + 1} t^{2 n} d t$ $= \frac{1}{2 n + 1} {(\frac{1}{\sqrt{2}})}^{2 n + 1} l n (\sqrt{2}) - \frac{1}{{(2 n + 1)}^{2}} \Rightarrow$ $\sum_{n = 0}^{\infty} A_{n} = l n (\sqrt{2}) \sum_{n = 0}^{\infty} \frac{1}{2 n + 1} {(\frac{1}{\sqrt{2}})}^{2 n + 1} - \sum_{n = 0}^{\infty} \frac{1}{{(2 n + 1)}^{2}}$ $\Rightarrow \int_{1}^{\sqrt{2}} \frac{l n (x)}{x^{2} - 1} d x = l n (\sqrt{2}) \sum_{n = 0}^{\infty} \frac{1}{{(2 n + 1)}^{2}} {(\frac{1}{\sqrt{2}})}^{2 n + 1}$ $- \frac{π^{2}}{8}$
Commented by prof Abdo imad last updated on 20/May/18
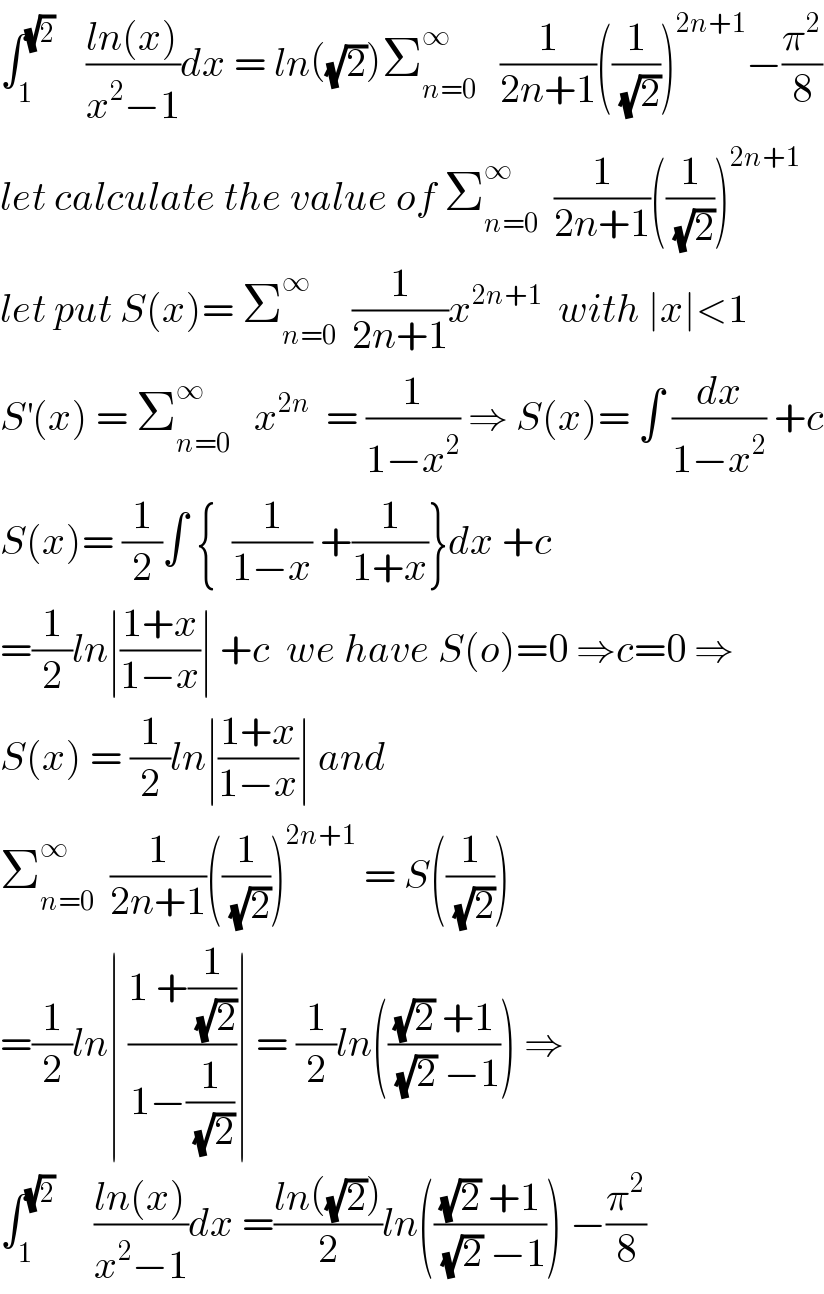
$∫_1 ^(√2) ((ln(x))/(x^2 −1))dx = ln((√2))Σ_(n=0) ^∞ (1/(2n+1))((1/(√2)))^(2n+1) −(π^2 /8) let calculate the value of Σ_(n=0) ^∞ (1/(2n+1))((1/(√2)))^(2n+1) let put S(x)= Σ_(n=0) ^∞ (1/(2n+1))x^(2n+1) with ∣x∣<1 S^′ (x) = Σ_(n=0) ^∞ x^(2n) = (1/(1−x^2 )) ⇒ S(x)= ∫ (dx/(1−x^2 )) +c S(x)= (1/2)∫ { (1/(1−x)) +(1/(1+x))}dx +c =(1/2)ln∣((1+x)/(1−x))∣ +c we have S(o)=0 ⇒c=0 ⇒ S(x) = (1/2)ln∣((1+x)/(1−x))∣ and Σ_(n=0) ^∞ (1/(2n+1))((1/(√2)))^(2n+1) = S((1/(√2))) =(1/2)ln∣ ((1 +(1/(√2)))/(1−(1/(√2))))∣ = (1/2)ln((((√2) +1)/((√2) −1))) ⇒ ∫_1 ^(√2) ((ln(x))/(x^2 −1))dx =((ln((√2)))/2)ln((((√2) +1)/((√2) −1))) −(π^2 /8)$
$\int_{1}^{\sqrt{2}} \frac{l n (x)}{x^{2} - 1} d x = l n (\sqrt{2}) \sum_{n = 0}^{\infty} \frac{1}{2 n + 1} {(\frac{1}{\sqrt{2}})}^{2 n + 1} - \frac{π^{2}}{8}$ $l e t c a l c u l a t e t h e v a l u e o f \sum_{n = 0}^{\infty} \frac{1}{2 n + 1} {(\frac{1}{\sqrt{2}})}^{2 n + 1}$ $l e t p u t S (x) = \sum_{n = 0}^{\infty} \frac{1}{2 n + 1} x^{2 n + 1} w i t h ∣ x ∣< 1$ $S^{^{'}} (x) = \sum_{n = 0}^{\infty} x^{2 n} = \frac{1}{1 - x^{2}} \Rightarrow S (x) = \int \frac{d x}{1 - x^{2}} + c$ $S (x) = \frac{1}{2} \int {\frac{1}{1 - x} + \frac{1}{1 + x}} d x + c$ $= \frac{1}{2} l n ∣ \frac{1 + x}{1 - x} ∣ + c w e h a v e S (o) = 0 \Rightarrow c = 0 \Rightarrow$ $S (x) = \frac{1}{2} l n ∣ \frac{1 + x}{1 - x} ∣ a n d$ $\sum_{n = 0}^{\infty} \frac{1}{2 n + 1} {(\frac{1}{\sqrt{2}})}^{2 n + 1} = S (\frac{1}{\sqrt{2}})$ $= \frac{1}{2} l n ∣ \frac{1 + \frac{1}{\sqrt{2}}}{1 - \frac{1}{\sqrt{2}}} ∣ = \frac{1}{2} l n (\frac{\sqrt{2} + 1}{\sqrt{2} - 1}) \Rightarrow$ $\int_{1}^{\sqrt{2}} \frac{l n (x)}{x^{2} - 1} d x = \frac{l n (\sqrt{2})}{2} l n (\frac{\sqrt{2} + 1}{\sqrt{2} - 1}) - \frac{π^{2}}{8}$
Commented by prof Abdo imad last updated on 20/May/18
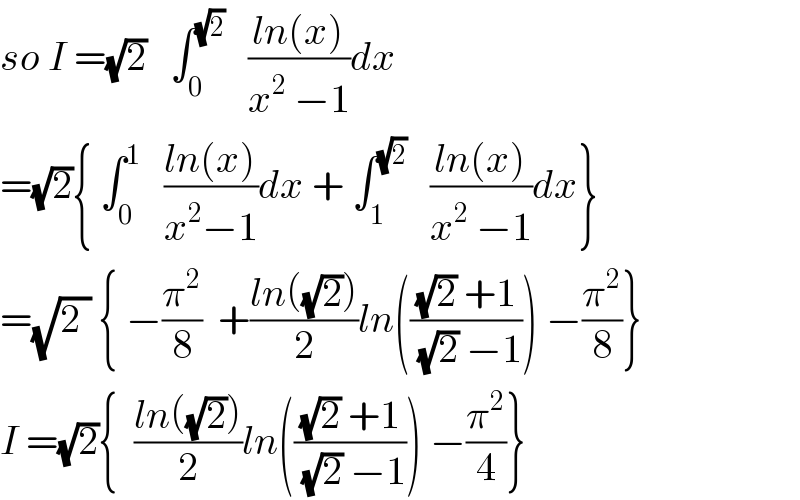
$so I =(√2) ∫_0 ^(√2) ((ln(x))/(x^2 −1))dx =(√2){ ∫_0 ^1 ((ln(x))/(x^2 −1))dx + ∫_1 ^(√2) ((ln(x))/(x^2 −1))dx} =(√2_ ) { −(π^2 /8) +((ln((√2)))/2)ln((((√2) +1)/((√2) −1))) −(π^2 /8)} I =(√2){ ((ln((√2)))/2)ln((((√2) +1)/((√2) −1))) −(π^2 /4)}$
$s o I = \sqrt{2} \int_{0}^{\sqrt{2}} \frac{l n (x)}{x^{2} - 1} d x$ $= \sqrt{2} {\int_{0}^{1} \frac{l n (x)}{x^{2} - 1} d x + \int_{1}^{\sqrt{2}} \frac{l n (x)}{x^{2} - 1} d x}$ $= \sqrt{2_{}} {- \frac{π^{2}}{8} + \frac{l n (\sqrt{2})}{2} l n (\frac{\sqrt{2} + 1}{\sqrt{2} - 1}) - \frac{π^{2}}{8}}$ $I = \sqrt{2} {\frac{l n (\sqrt{2})}{2} l n (\frac{\sqrt{2} + 1}{\sqrt{2} - 1}) - \frac{π^{2}}{4}}$
	Answered by math1967 last updated on 17/May/18

	$\underset{0}{\int^{π}} \frac{x d x}{3 + 2 \cos^{2} \frac{x}{2} - 1} = \underset{0}{\int^{π}} \frac{x d x}{2 (1 + \cos^{2} \frac{x}{2})}$ $n o w 2 I = π \underset{0}{\int^{π}} \frac{d x}{2 (1 + {c o s}^{2} \frac{x}{2})}$ $= \frac{π}{2} \underset{0}{\int^{π}} \frac{\sec^{2} \frac{x}{2} d x}{\sec^{2} \frac{x}{2} + 1}$ $= π \underset{0}{\int^{π}} \frac{\frac{1}{2} \sec^{2} \frac{x}{2} d x}{2 + {t a n}^{2} \frac{x}{2}}$ $= π \underset{0}{\int^{π}} \frac{d (t a n \frac{x}{2})}{{(\sqrt{2})}^{2} + {t a n}^{2} \frac{x}{2}} = π {[\frac{1}{\sqrt{2}} \tan^{- 1} \tan \frac{x}{2 \sqrt{2}}]}_{0}^{π}$ $= π \times [\frac{1}{\sqrt{2}} \times \frac{π}{2 \sqrt{2}}] = \frac{π^{2}}{4} ∴ I = \frac{π^{2}}{8}$ $p l z . c h e c k$
	Commented by MJS last updated on 17/May/18

	$in this case if f (x) = \frac{\frac{x}{2}}{1 + \cos^{2} \frac{x}{2}} \Rightarrow$ $\Rightarrow f (π - x) = \frac{\frac{π - x}{2}}{1 + \sin^{2} \frac{x}{2}}$ $and we get f (x) + f (π - x) =$ $= \frac{3 π}{8 + \sin^{2} x} + \frac{π \cos x}{8 + \sin^{2} x} - \frac{2 x \cos x}{8 + \sin^{2} x}$ $we can solve the 1^{st} and 2^{nd} but the 3^{rd} looks$ $nasty again . . .$
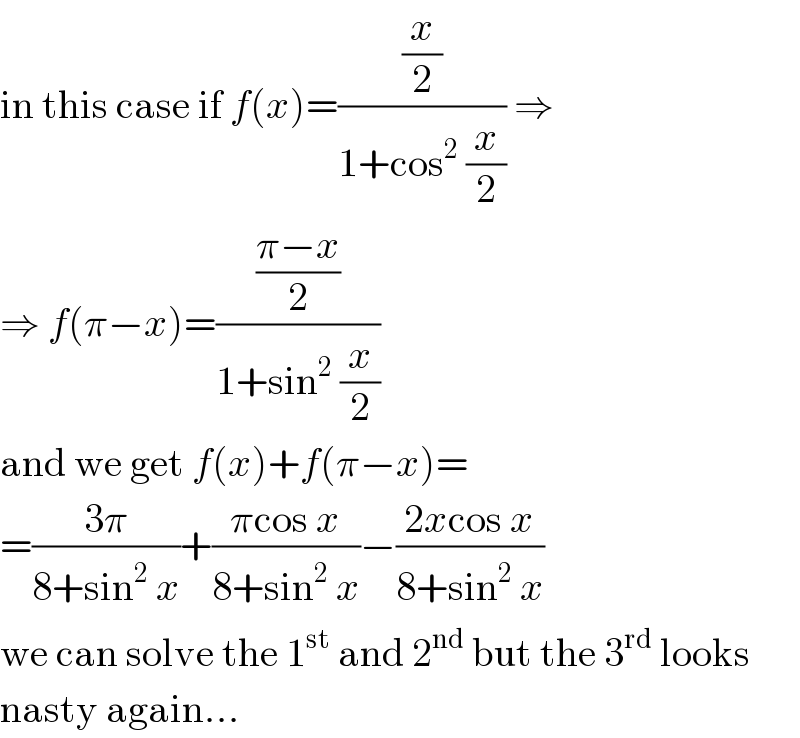
	Commented by math1967 last updated on 17/May/18

	$O K t h a n k s$
	Answered by math1967 last updated on 17/May/18

	$2 I = \underset{0}{\int^{π}} \frac{x d x}{3 + c o s x} + \underset{0}{\int^{π}} \frac{(π - x) d x}{3 + c o s (π - x)}$ $= π \underset{0}{\int^{π}} \frac{6 d x}{(3 + c o s x) (3 - c o s x)}$ $= 6 π \underset{0}{\int^{π}} \frac{d x}{9 - {c o s}^{2} x} = 6 π \underset{0}{\int^{π}} \frac{\sec^{2} x d x}{9 {s e c}^{2} x - 1}$ $= 6 π \underset{0}{\int^{π}} \frac{{s e c}^{2} x d x}{8 + 9 \tan^{2} x} = 2 π \underset{0}{\int^{π}} \frac{3 \sec^{2} x d x}{{(2 \sqrt{2})}^{2} + {(3 \tan x)}^{2}}$ $= 2 π \underset{0}{\int^{π}} \frac{d (3 t a n x)}{{(2 \sqrt{2})}^{2} + {(3 \tan x)}^{2}}$ $= 2 π {[\frac{1}{2 \sqrt{2}} \tan^{- 1} \frac{3 \tan x}{2 \sqrt{2}}]}_{0}^{π}$ $= 2 π [\frac{1}{2 \sqrt{2}} \times \frac{π}{2} - 0]$ $= \frac{π^{2}}{2 \sqrt{2}} ∴ I = \frac{π^{2}}{4 \sqrt{2}}$
	Commented by MJS last updated on 17/May/18

	$this seems wrong :$ $\frac{x}{3 + \cos x} + \frac{π - x}{3 + \cos (π - x)} = \frac{x}{3 + \cos x} + \frac{π - x}{3 - \cos x} =$ $= \frac{3 π + (π - 2 x) \cos x}{9 - \cos^{2} x} \neq \frac{6 π}{9 - \cos^{2} x}$ $please explain$ $\frac{π^{2}}{4 \sqrt{2}} \approx 1.744716$ $but I get \underset{0}{\int^{π}} \frac{x}{3 + \cos x} d x \approx 1.988159$
	Commented by math1967 last updated on 17/May/18

	$Y e s i t i s m y m i s t a k e$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum