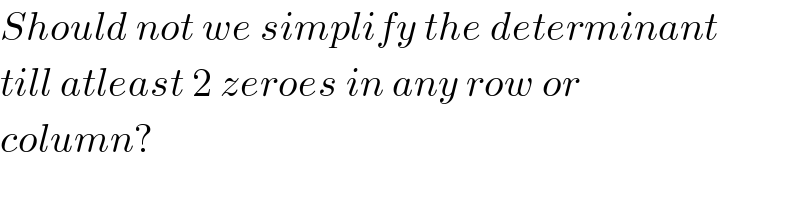Math Question and Answers


Question and Answers Forum

All Questions Topic List
Matrices and Determinants Questions
Previous in All Question Next in All Question
Previous in Matrices and Determinants Next in Matrices and Determinants
Question Number 35319 by Tinkutara last updated on 17/May/18

	Answered by MJS last updated on 17/May/18

	${it}^{'} s just multiplicating and factorising$ $\det \| \begin{matrix} a & b & c \\ d & e & f \\ g & h & i \end{matrix} \| = a e i + b f g + c d h - a f h - b d i - c e g$
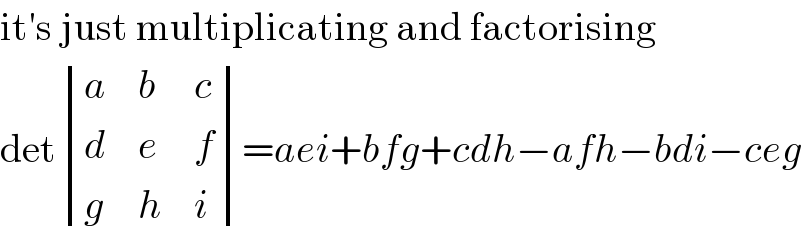
	Commented by Tinkutara last updated on 18/May/18
	No it is to be done by properties of determinants. Please can you try that way?
	Answered by ajfour last updated on 18/May/18
	$determinant ((((b+c)^2 ),a^2 ,a^2 ),(b^2 ,((c+a)^2 ),b^2 ),(c^2 ,c^2 ,((a+b)^2 ))) C_1 →C_1 −C_3 ; C_2 →C_2 −C_3 = determinant ((((b+c+a)(b+c−a)),0,a^2 ),(0,((c+a+b)(c+a−b)),b^2 ),(((c+a+b)(c−a−b)),((c+a+b)(c−a−b)),((a+b)^2 ))) =(a+b+c)^2 determinant (((b+c−a),0,a^2 ),(0,(c+a−b),b^2 ),((c−a−b),(c−a−b),((a+b)^2 ))) R_3 →R_3 −(R_1 +R_2 ) =(a+b+c)^2 determinant (((b+c−a),0,a^2 ),(0,(c+a−b),b^2 ),((−2b),(−2a),(2ab))) =(a+b+c)^2 {(b+c−a)[2abc+2a^2 b] +a^2 [2bc+2ab−2b^2 ]} =(a+b+c)^2 {2b[abc+ac^2 −a^2 c a^2 b+a^2 c−a^3 +a^2 c+a^3 −a^2 b]} =(a+b+c)^2 {2b[abc+ac^2 +a^2 c} =2abc(a+b+c)^2 (b+c+a) =2abc(a+b+c)^3 .$
	$\| \begin{matrix} {(b + c)}^{2} & a^{2} & a^{2} \\ b^{2} & {(c + a)}^{2} & b^{2} \\ c^{2} & c^{2} & {(a + b)}^{2} \end{matrix} \|$ $C_{1} \to C_{1} - C_{3}; C_{2} \to C_{2} - C_{3}$ $= \| \begin{matrix} (b + c + a) (b + c - a) & 0 & a^{2} \\ 0 & (c + a + b) (c + a - b) & b^{2} \\ (c + a + b) (c - a - b) & (c + a + b) (c - a - b) & {(a + b)}^{2} \end{matrix} \|$ $= {(a + b + c)}^{2} \| \begin{matrix} b + c - a & 0 & a^{2} \\ 0 & c + a - b & b^{2} \\ c - a - b & c - a - b & {(a + b)}^{2} \end{matrix} \|$ $R_{3} \to R_{3} - (R_{1} + R_{2})$ $= {(a + b + c)}^{2} \| \begin{matrix} b + c - a & 0 & a^{2} \\ 0 & c + a - b & b^{2} \\ - 2 b & - 2 a & 2 a b \end{matrix} \|$ $= {(a + b + c)}^{2} {(b + c - a) [2 a b c + 2 a^{2} b]$ $+ a^{2} [2 b c + 2 a b - 2 b^{2}]}$ $= {(a + b + c)}^{2} {2 b [a b c + {a c}^{2} - a^{2} c$ $a^{2} b + a^{2} c - a^{3} + a^{2} c + a^{3} - a^{2} b]}$ $= {(a + b + c)}^{2} {2 b [a b c + {a c}^{2} + a^{2} c}$ $= 2 a b c {(a + b + c)}^{2} (b + c + a)$ $= 2 a b c {(a + b + c)}^{3} .$
	Commented by tanmay.chaudhury50@gmail.com last updated on 18/May/18

	$p l s l e t m e k n o w h o w t o p u t d e t e r m i n a n t s i g n$ $i n t h i s a p p$
	Commented by ajfour last updated on 18/May/18

	$i {c o u l d n}^{'} t f i n d a w a y l i k e t h a t . .$
	Commented by Tinkutara last updated on 18/May/18

	$S h o u l d n o t w e s i m p l i f y t h e d e t e r m i n a n t$ $t i l l a t l e a s t 2 z e r o e s i n a n y r o w o r$ $c o l u m n ?$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum