
Question and Answers Forum
Question Number 35384 by 7991 last updated on 18/May/18
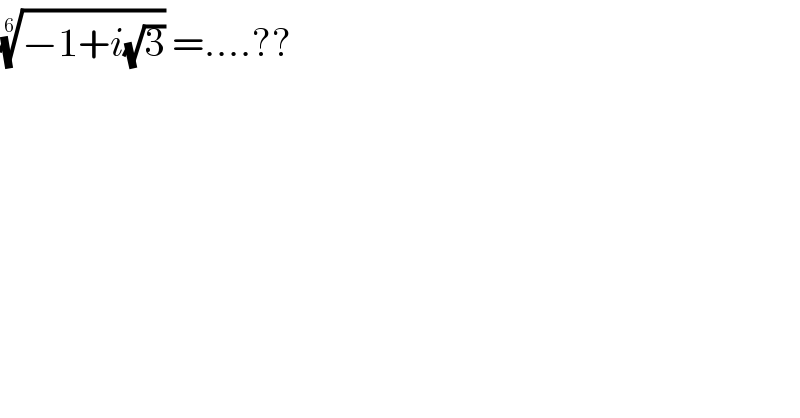
Commented by prof Abdo imad last updated on 18/May/18
![the 6^(eme) roots of −1+i(√3) are the complex z_k wich verify z_k ^6 = −1+i(√3) let solve z^6 =−1+i(√3) z=r e^(iθ) ∣−1+i(√3)∣=2 ⇒−1+i(√3) =2(−(1/2) +i((√3)/2)) =2e^(i((2π)/3)) so z^6 =−1+i(√3) ⇔r^6 e^(i(6θ)) = 2 e^(i((2π)/3)) ⇒ r = 2^(1/6) and 6θ= ((2π)/3) +2kπ ⇒r=^6 (√2) θ= (π/9) +((kπ)/3) k∈[[0,5]]⇒ z_k =^6 (√2) e^(i((π/9) +((kπ)/3))) with k∈[0,5] .](Q35393.png)
Answered by MJS last updated on 18/May/18
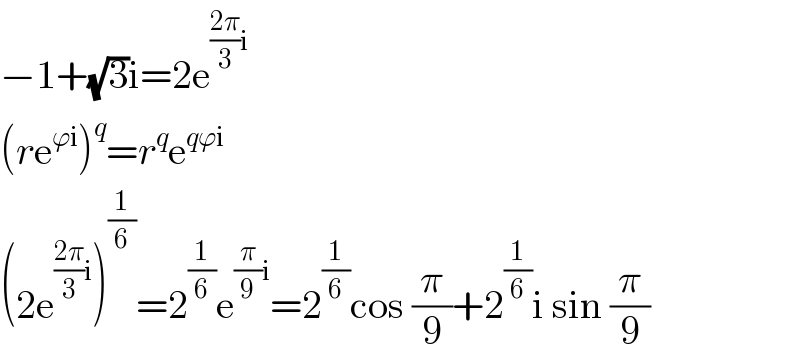
| ||
Question and Answers Forum | ||
Question Number 35384 by 7991 last updated on 18/May/18 | ||
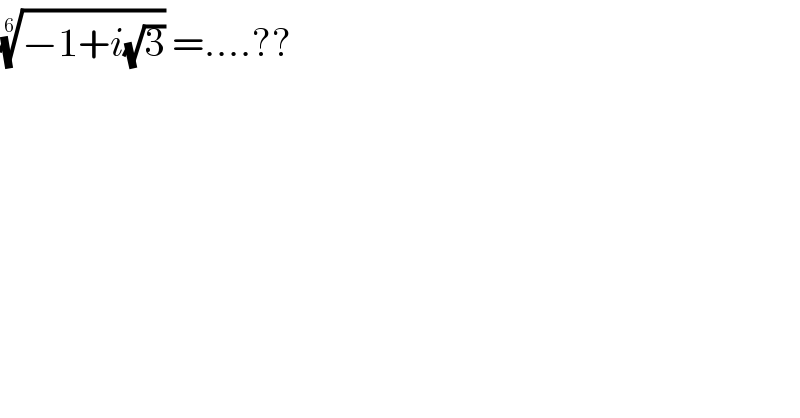 | ||
Commented by prof Abdo imad last updated on 18/May/18 | ||
![the 6^(eme) roots of −1+i(√3) are the complex z_k wich verify z_k ^6 = −1+i(√3) let solve z^6 =−1+i(√3) z=r e^(iθ) ∣−1+i(√3)∣=2 ⇒−1+i(√3) =2(−(1/2) +i((√3)/2)) =2e^(i((2π)/3)) so z^6 =−1+i(√3) ⇔r^6 e^(i(6θ)) = 2 e^(i((2π)/3)) ⇒ r = 2^(1/6) and 6θ= ((2π)/3) +2kπ ⇒r=^6 (√2) θ= (π/9) +((kπ)/3) k∈[[0,5]]⇒ z_k =^6 (√2) e^(i((π/9) +((kπ)/3))) with k∈[0,5] .](Q35393.png) | ||
Answered by MJS last updated on 18/May/18 | ||
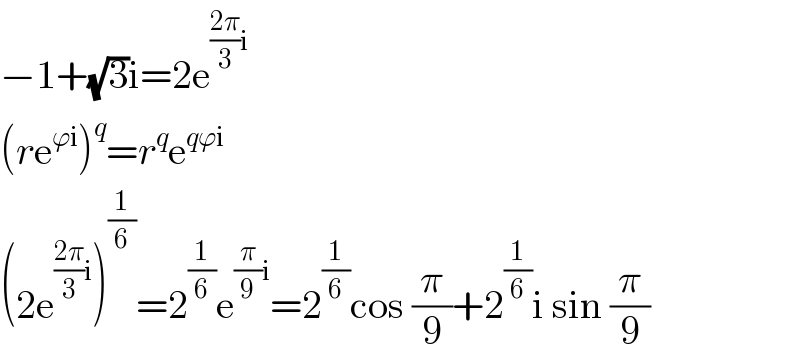 | ||
| ||