
Question and Answers Forum
Question Number 35429 by abdo.msup.com last updated on 18/May/18
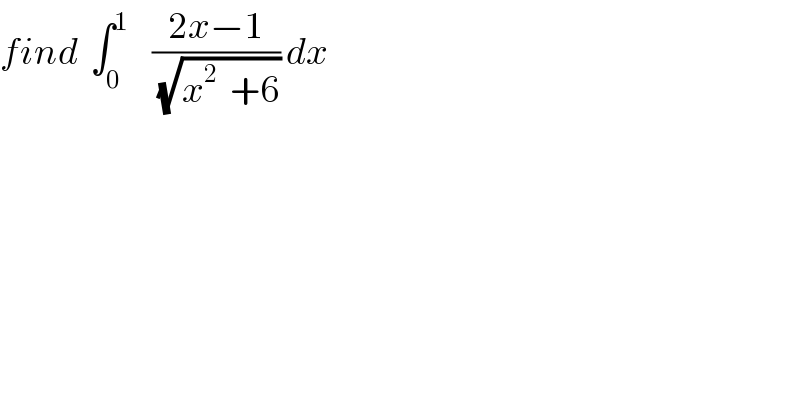
Commented by prof Abdo imad last updated on 19/May/18
![let put I = ∫_0 ^1 ((2x−1)/(√(x^2 +6))) .changement x=(√6)sht give I = ∫_0 ^(argsh((1/(√6)))) ((2(√6) sht −1)/((√6)ch(t))) (√6) cht dt = ∫_0 ^(ln( (1/(√6)) +(√(1+(1/6)))) (2(√6) sh(t)−1)dt =2(√6) [ ch(t)]_0 ^(ln( (1/(√6)) +(√(7/6)))) −ln((1/(√6)) +((√7)/(√6))) we have ch(t) =((e^t +e^(−t) )/2) ⇒ ch{ ln( (1/(√6)) +((√7)/(√6)))} = ((((1/(√6)) +((√7)/(√6))) +((1/(√6))+((√7)/(√6)))^(−1) )/2) ⇒ I = 2(√6){ ((((1/(√6))+((√7)/(√6))) +((1/(√6)) +((√7)/(√6)))^(−1) )/2) −1} −ln((1/(√6)) +((√7)/(√6)))](Q35449.png)
Answered by ajfour last updated on 19/May/18
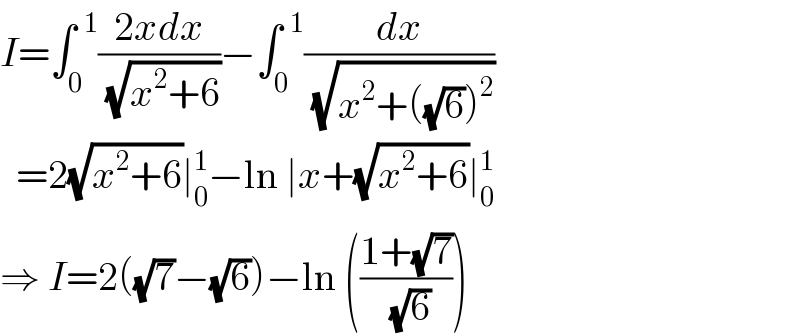
| ||
Question and Answers Forum | ||
Question Number 35429 by abdo.msup.com last updated on 18/May/18 | ||
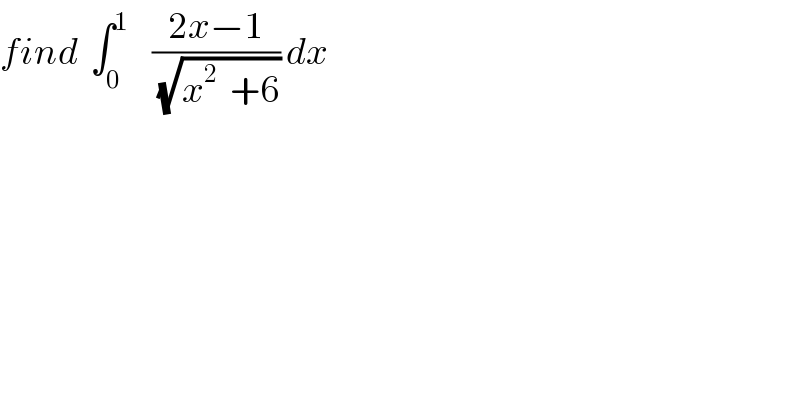 | ||
Commented by prof Abdo imad last updated on 19/May/18 | ||
![let put I = ∫_0 ^1 ((2x−1)/(√(x^2 +6))) .changement x=(√6)sht give I = ∫_0 ^(argsh((1/(√6)))) ((2(√6) sht −1)/((√6)ch(t))) (√6) cht dt = ∫_0 ^(ln( (1/(√6)) +(√(1+(1/6)))) (2(√6) sh(t)−1)dt =2(√6) [ ch(t)]_0 ^(ln( (1/(√6)) +(√(7/6)))) −ln((1/(√6)) +((√7)/(√6))) we have ch(t) =((e^t +e^(−t) )/2) ⇒ ch{ ln( (1/(√6)) +((√7)/(√6)))} = ((((1/(√6)) +((√7)/(√6))) +((1/(√6))+((√7)/(√6)))^(−1) )/2) ⇒ I = 2(√6){ ((((1/(√6))+((√7)/(√6))) +((1/(√6)) +((√7)/(√6)))^(−1) )/2) −1} −ln((1/(√6)) +((√7)/(√6)))](Q35449.png) | ||
Answered by ajfour last updated on 19/May/18 | ||
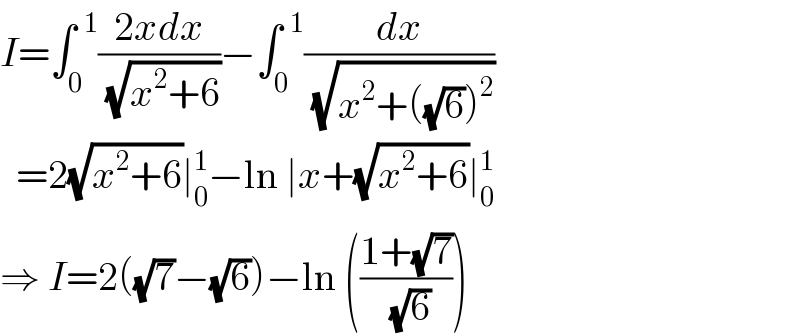 | ||
| ||