
Question and Answers Forum
Question Number 35440 by prof Abdo imad last updated on 19/May/18
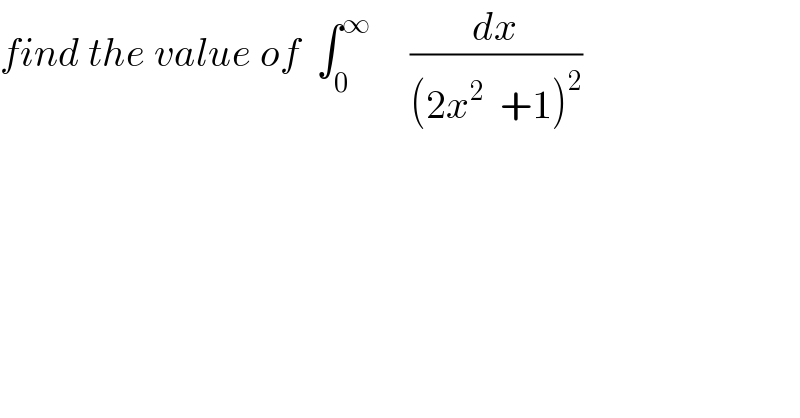
Commented by prof Abdo imad last updated on 19/May/18
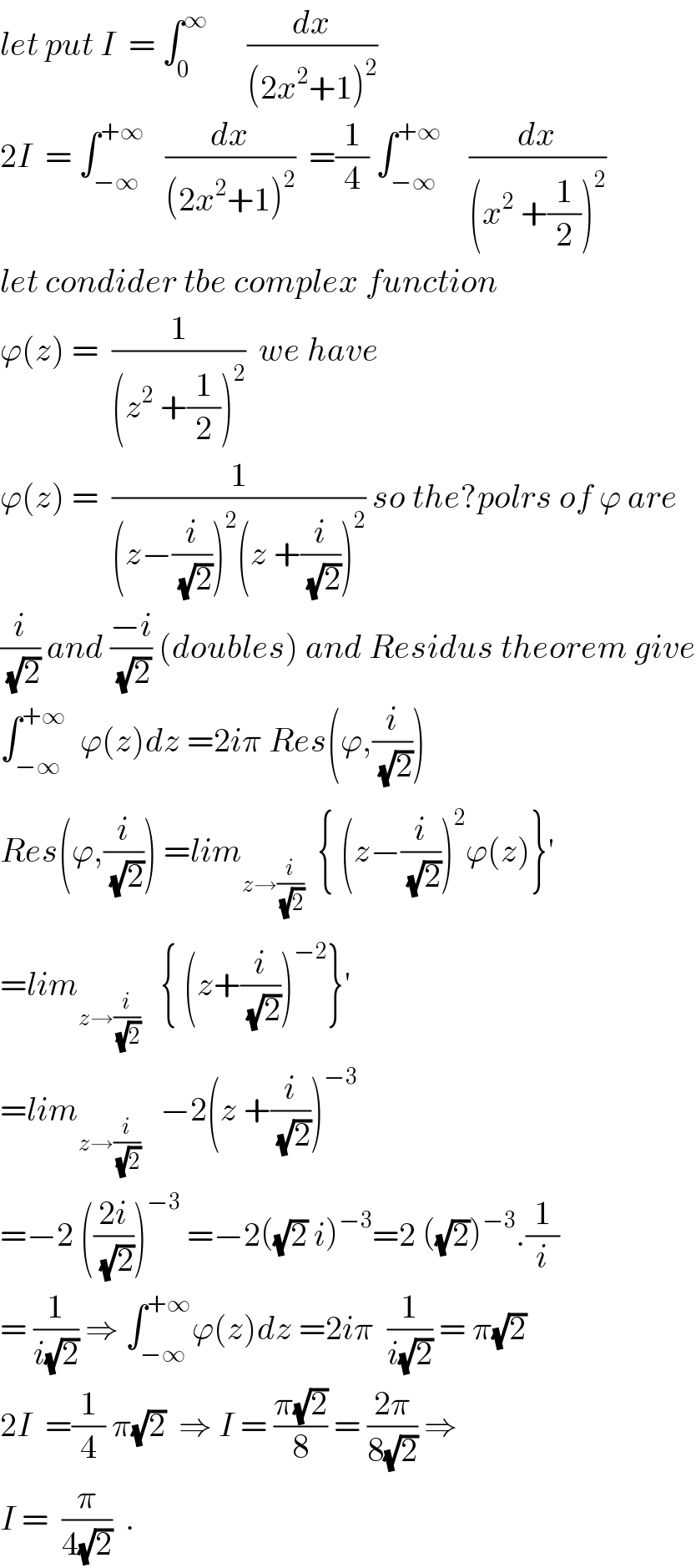
Commented by prof Abdo imad last updated on 19/May/18
![I = ∫_0 ^∞ (dx/((2x^2 +1)^2 )) let use the changement x=(1/(√2)) tant ⇒ I = (1/(√2))∫_0 ^(π/2) ((1+tan^2 t)/((1+tan^2 )^2 ))dt = (1/(√2)) ∫_0 ^(π/2) (dt/(1+tan^2 t)) = (1/(√2)) ∫_0 ^(π/2) cos^2 t dt =(1/(√2)) ∫_0 ^(π/2) (((1+cos(2t))/2))dt = (1/(2(√2))) (π/2) + (1/(4(√2)))[ sin(2t)]_0 ^(π/2) ★ I = (π/(4(√2))) ★](Q35501.png)
Answered by ajfour last updated on 19/May/18
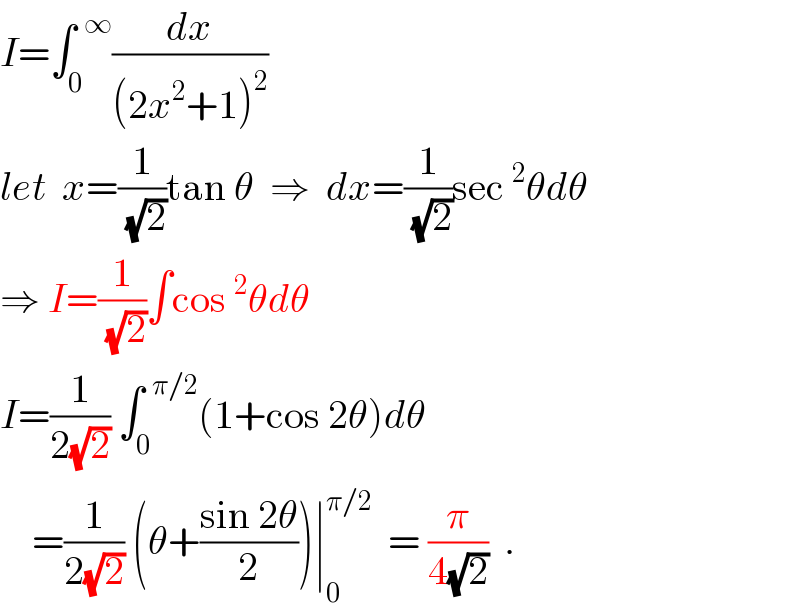
| ||
Question and Answers Forum | ||
Question Number 35440 by prof Abdo imad last updated on 19/May/18 | ||
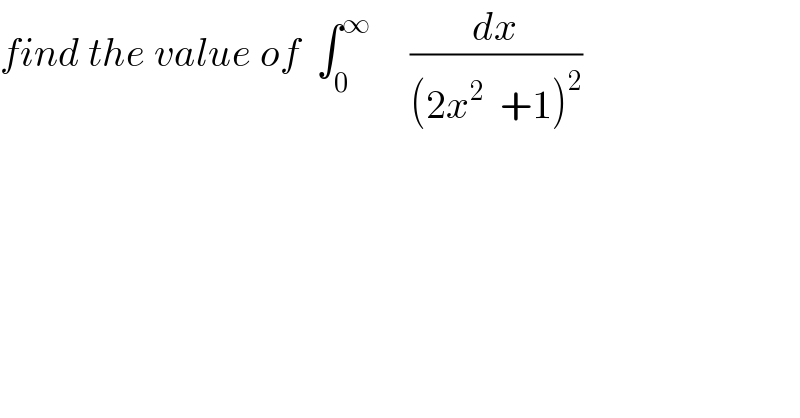 | ||
Commented by prof Abdo imad last updated on 19/May/18 | ||
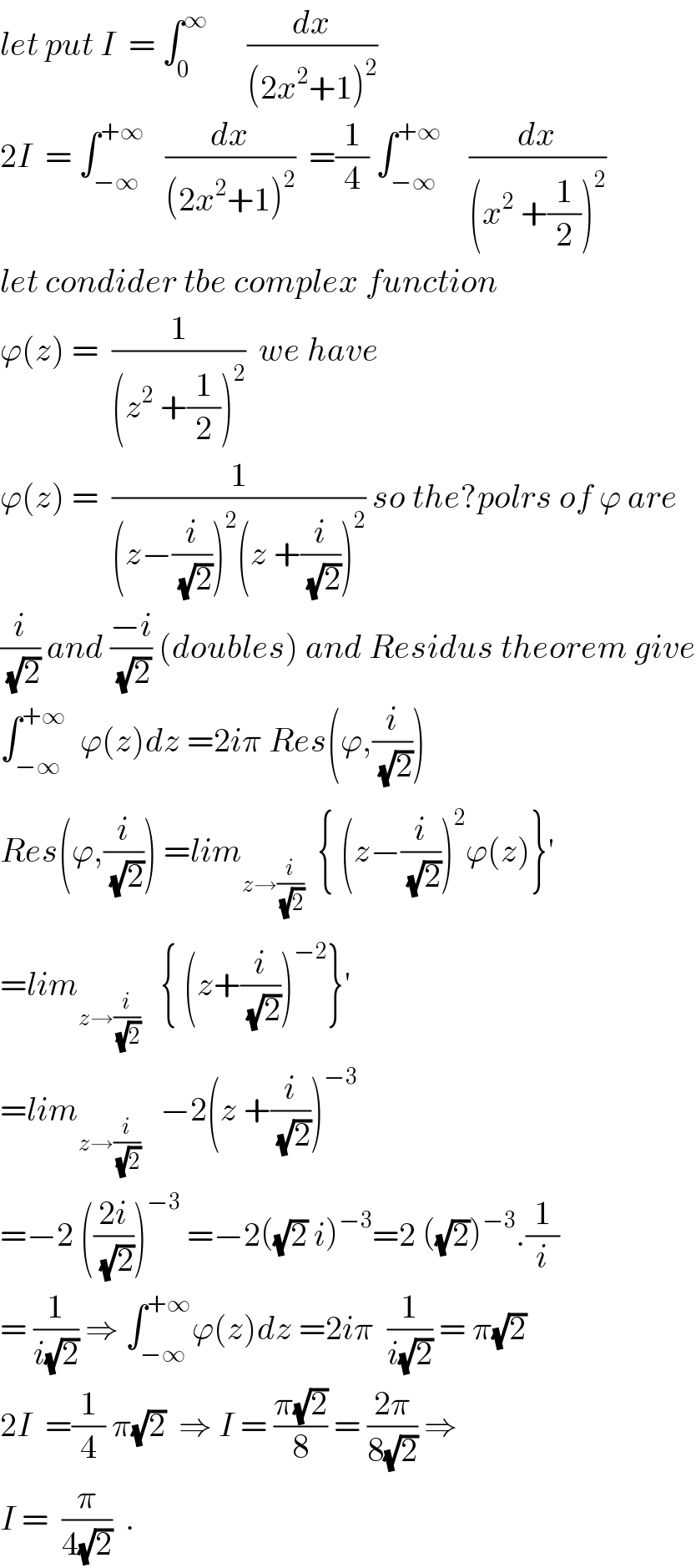 | ||
Commented by prof Abdo imad last updated on 19/May/18 | ||
![I = ∫_0 ^∞ (dx/((2x^2 +1)^2 )) let use the changement x=(1/(√2)) tant ⇒ I = (1/(√2))∫_0 ^(π/2) ((1+tan^2 t)/((1+tan^2 )^2 ))dt = (1/(√2)) ∫_0 ^(π/2) (dt/(1+tan^2 t)) = (1/(√2)) ∫_0 ^(π/2) cos^2 t dt =(1/(√2)) ∫_0 ^(π/2) (((1+cos(2t))/2))dt = (1/(2(√2))) (π/2) + (1/(4(√2)))[ sin(2t)]_0 ^(π/2) ★ I = (π/(4(√2))) ★](Q35501.png) | ||
Answered by ajfour last updated on 19/May/18 | ||
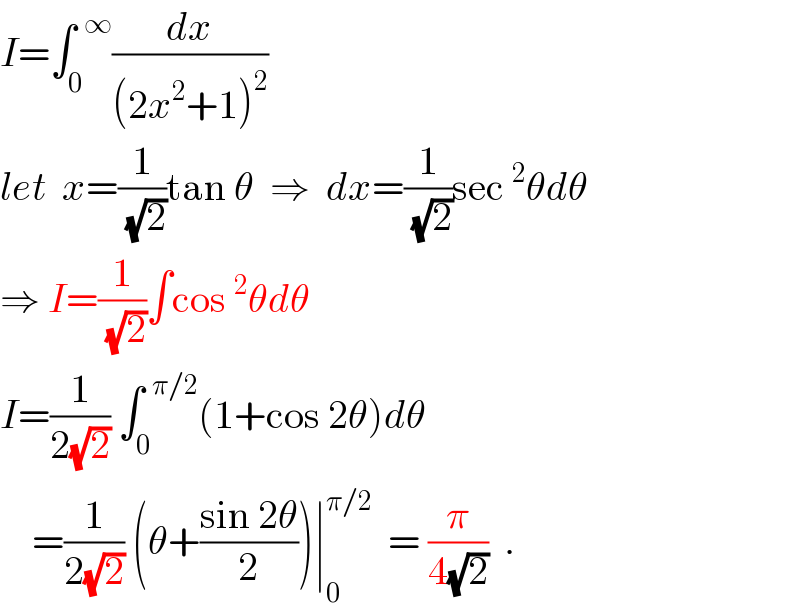 | ||
| ||