
Question and Answers Forum
Question Number 35456 by math1967 last updated on 19/May/18

Answered by ajfour last updated on 19/May/18

Answered by tanmay.chaudhury50@gmail.com last updated on 19/May/18
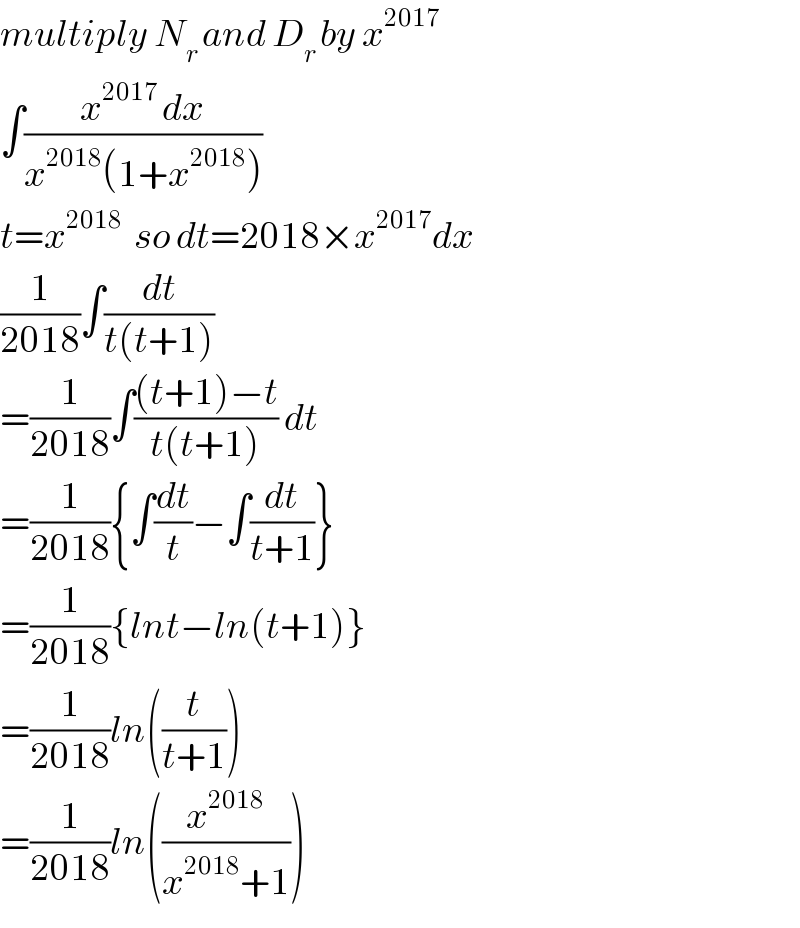
| ||
Question and Answers Forum | ||
Question Number 35456 by math1967 last updated on 19/May/18 | ||
 | ||
Answered by ajfour last updated on 19/May/18 | ||
 | ||
| ||
Answered by tanmay.chaudhury50@gmail.com last updated on 19/May/18 | ||
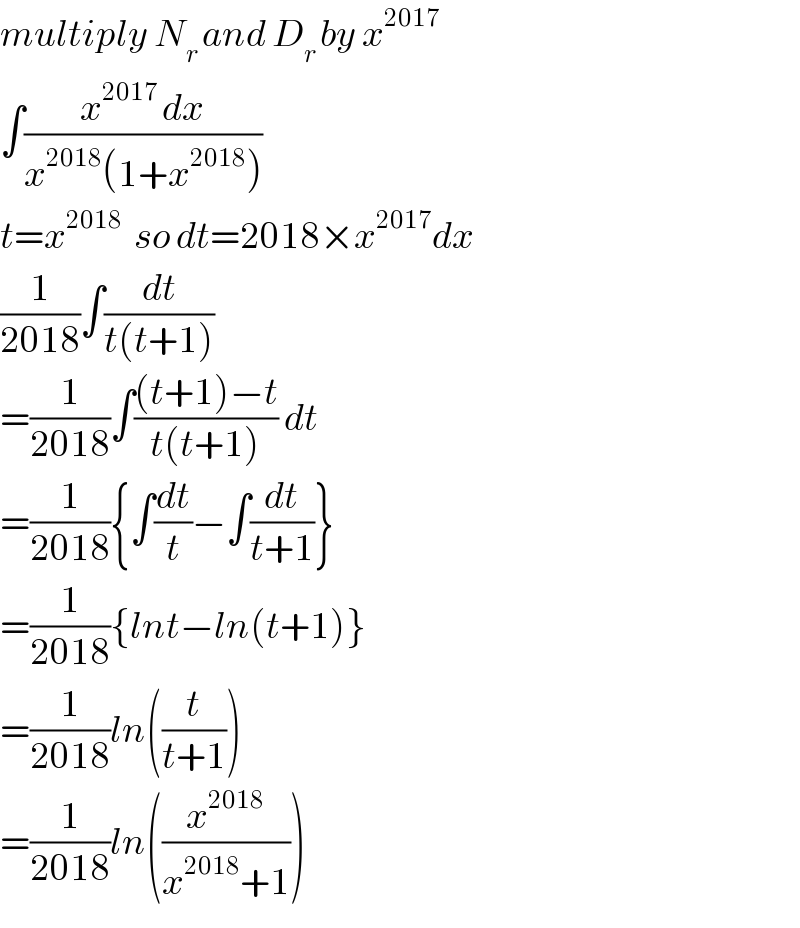 | ||
| ||