
Question and Answers Forum
Question Number 35589 by abdo mathsup 649 cc last updated on 20/May/18
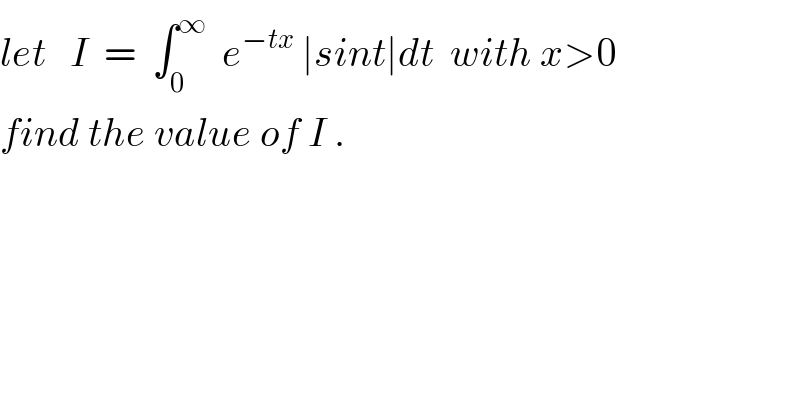
Commented byabdo mathsup 649 cc last updated on 21/May/18
![I = Σ_(n=0) ^∞ ∫_(nπ) ^((n+1)π) e^(−tx) ∣sint∣dt changement t =nπ + u give I = Σ_(n=0) ^∞ ∫_0 ^π e^(−nπx) e^(−xu) ∣sinu∣du = Σ_(n=0) ^∞ e^(−nπx) ∫_0 ^π e^(−xu) sinu du but A(x)=∫_0 ^π e^(−xu) sin(u)du =Im( ∫_0 ^π e^(−xu +iu) du) =Im( ∫_0 ^π e^((−x+i)u) du) but ∫_0 ^π e^((−x+i)u) du =[ (1/(−x+i)) e^((−x+i)u) ]_0 ^π =((−1)/(x−i)){ e^(−xπ +iπ) −1}= ((1 +e^(−πx) )/(x−i)) =((x+i)/(x^2 +1))( 1+e^(−πx) )⇒ A(x)= ((1+e^(−πx) )/(1+x^2 )) Σ_(n=0) ^∞ e^(−nπx) = Σ_(n=0) ^∞ (e^(−πx) )^n = (1/(1−e^(−πx) )) so I = (1/(1−e^(−πx) )) ((1 +e^(−πx) )/(1+x^2 )) ⇒ I = ((1+e^(−πx) )/((1+x^2 )(1−e^(−πx) ))) .](Q35661.png)
| ||
Question and Answers Forum | ||
Question Number 35589 by abdo mathsup 649 cc last updated on 20/May/18 | ||
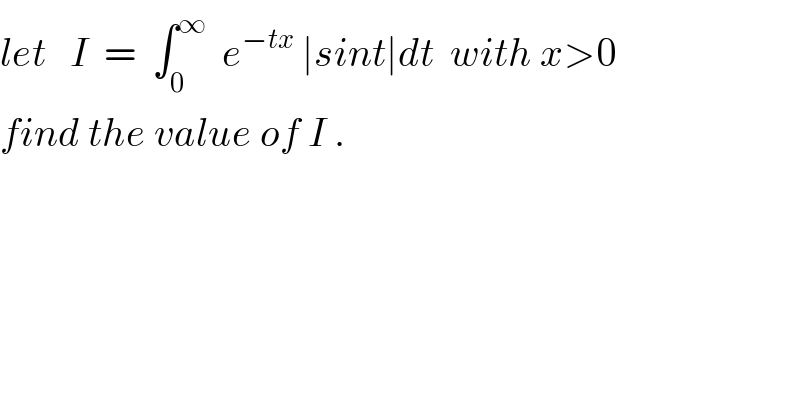 | ||
Commented byabdo mathsup 649 cc last updated on 21/May/18 | ||
![I = Σ_(n=0) ^∞ ∫_(nπ) ^((n+1)π) e^(−tx) ∣sint∣dt changement t =nπ + u give I = Σ_(n=0) ^∞ ∫_0 ^π e^(−nπx) e^(−xu) ∣sinu∣du = Σ_(n=0) ^∞ e^(−nπx) ∫_0 ^π e^(−xu) sinu du but A(x)=∫_0 ^π e^(−xu) sin(u)du =Im( ∫_0 ^π e^(−xu +iu) du) =Im( ∫_0 ^π e^((−x+i)u) du) but ∫_0 ^π e^((−x+i)u) du =[ (1/(−x+i)) e^((−x+i)u) ]_0 ^π =((−1)/(x−i)){ e^(−xπ +iπ) −1}= ((1 +e^(−πx) )/(x−i)) =((x+i)/(x^2 +1))( 1+e^(−πx) )⇒ A(x)= ((1+e^(−πx) )/(1+x^2 )) Σ_(n=0) ^∞ e^(−nπx) = Σ_(n=0) ^∞ (e^(−πx) )^n = (1/(1−e^(−πx) )) so I = (1/(1−e^(−πx) )) ((1 +e^(−πx) )/(1+x^2 )) ⇒ I = ((1+e^(−πx) )/((1+x^2 )(1−e^(−πx) ))) .](Q35661.png) | ||