Question and Answers Forum
Question Number 35630 by abdo mathsup 649 cc last updated on 21/May/18
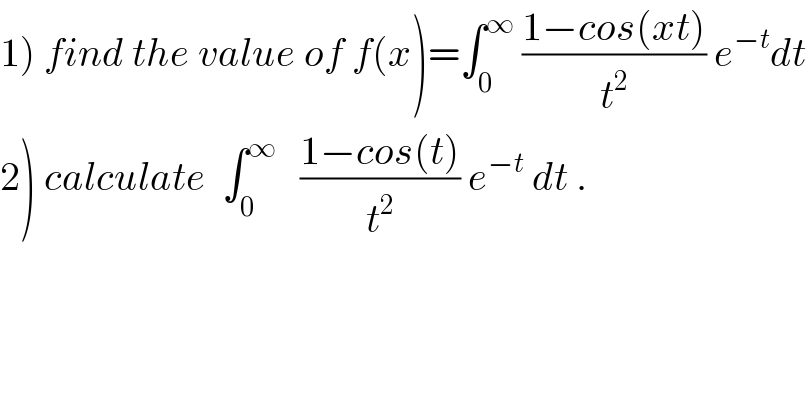
Commented by abdo mathsup 649 cc last updated on 24/May/18
![by parts u^′ = (1/t^2 ) and v =(1−cos(xt))e^(−t) ⇒ v^′ = xsin(xt) e^(−t) −(1−cos(xt))e^(−t) =( x sin(xt) +cos(xt)−1) e^(−t) f(x) = [ −(1/t) (1−cos(xt))e^(−t) ]_0 ^(+∞) −∫_0 ^∞ ((−1)/t) ( xsin(xt) +cos(xt) −1)e^(−t) dt but 1−cos(xt) ∼ ((x^2 t^2 )/2) ⇒ ((1−cos(xt))/t) ∼ ((tx^2 )/2) ⇒ lim_(t→0) (((1−cos(xt))e^(−t) )/t) =0 ⇒ f(x) = x ∫_0 ^∞ ((sin(xt))/t) e^(−t) dt +∫_0 ^∞ ((1−cos(xt))/t) e^(−t) dt let calculate h(x)= ∫_0 ^∞ ((sin(xt))/t) e^(−t) dt h^′ (x) = ∫_0 ^∞ cos(xt) e^(−t) dt =Re(∫_0 ^∞ e^(ixt−t) dt) ∫_0 ^∞ e^((−1 +ix)t) dt = [ (1/(−1+ix)) e^((−1+ix)t) ]_0 ^(+∞) = (1/(−1+ix)) = ((−1)/(1−ix)) = ((−1−ix)/(1+x^2 )) ⇒ h^′ (x) = ((−1)/(1+x^2 )) ⇒ h(x) =λ −arctan(x) but λ =h(0)=0 ⇒ h(x) =−arctan(x)](Q35813.png)
Commented by abdo mathsup 649 cc last updated on 24/May/18

Commented by abdo mathsup 649 cc last updated on 24/May/18
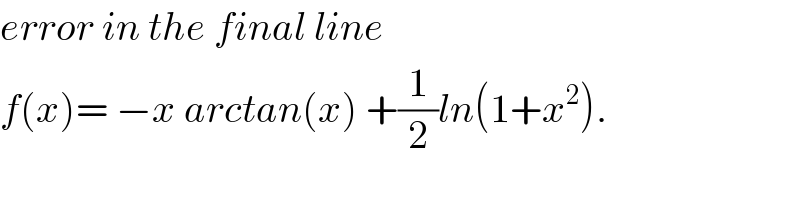
Commented by abdo mathsup 649 cc last updated on 24/May/18
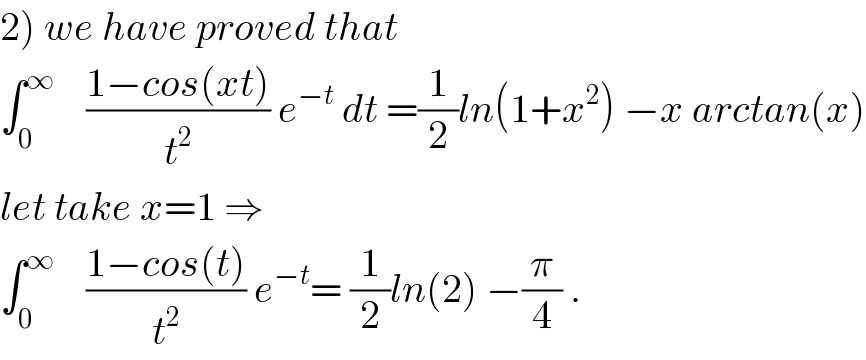
Commented by abdo mathsup 649 cc last updated on 24/May/18