
Question Number 35632 by abdo mathsup 649 cc last updated on 21/May/18
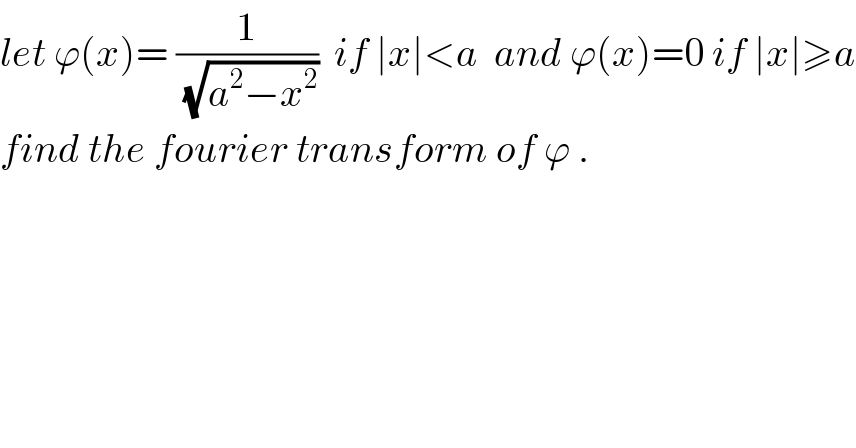
$${let}\:\varphi\left({x}\right)=\:\frac{\mathrm{1}}{\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }}\:\:{if}\:\mid{x}\mid<{a}\:\:{and}\:\varphi\left({x}\right)=\mathrm{0}\:{if}\:\mid{x}\mid\geqslant{a} \\ $$ $${find}\:{the}\:{fourier}\:{transform}\:{of}\:\varphi\:. \\ $$
Commented byabdo mathsup 649 cc last updated on 21/May/18
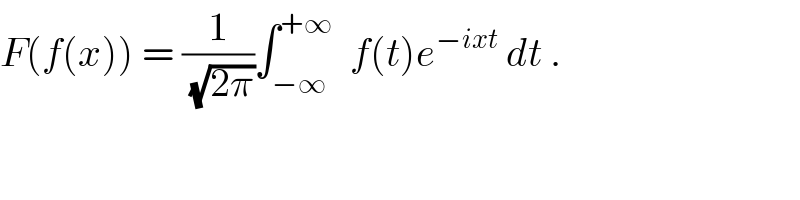
$${F}\left({f}\left({x}\right)\right)\:=\:\frac{\mathrm{1}}{\sqrt{\mathrm{2}\pi}}\int_{−\infty} ^{+\infty} \:\:{f}\left({t}\right){e}^{−{ixt}} \:{dt}\:. \\ $$
Commented byabdo mathsup 649 cc last updated on 24/May/18
![we have F(ϕ(x))= (1/(√(2π))) ∫_(−∞) ^(+∞) ϕ(t) e^(−ixt) dt and ϕ is even F(ϕ(x))o= (1/(√(2π))) ∫_(−∞) ^(+∞) ϕ(t) e^(−ixt) dt =(1/(√(2π))) ∫_(−a) ^a (e^(−ixt) /(√(a^2 −t^2 ))) dt =(√(2/π)) ∫_0 ^a ((cos(xt))/(√(a^2 −t^2 )))dt let find w(x) =∫_0 ^a ((cos(xt))/(√(a^2 −t^2 )))dt we hsve w^′ (x) = ∫_0 ^a ((−t sin(xt))/(√(a^2 −t^2 ))) and by parts w^′ (x) = [ (√(a^2 −t^2 )) sin(xt)]_0 ^a −∫_0 ^a (√(a^2 −t^2 )) x cos(xt)dt = −x ∫_0 ^a (√(a^2 −t^2 )) cos(xt)dt chsngement t =asinα give w^′ (x) = ∫_0 ^(π/2) a cos(α)cos(ax sinα) a cosα dα = a^2 ∫_0 ^(π/2) cos^2 (α) cos(ax sinα)dα =a^2 ∫_0 ^(π/2) cos(α) (cos(α) cos(ax sinα))dα =a^2 { (1/(ax)) sin(ax sin(α))cos(α)]_0 ^(π/2) − ∫_0 ^(π/2) −sin(α) sin(ax sinα) dα} = ∫_0 ^(π/2) sin(α) sin(ax sinα)dα ....be continued...](Q35812.png)
$${we}\:{have}\:{F}\left(\varphi\left({x}\right)\right)=\:\frac{\mathrm{1}}{\sqrt{\mathrm{2}\pi}}\:\int_{−\infty} ^{+\infty} \:\varphi\left({t}\right)\:{e}^{−{ixt}} \:{dt}\:{and}\:\varphi\:{is}\:{even} \\ $$ $${F}\left(\varphi\left({x}\right)\right){o}=\:\frac{\mathrm{1}}{\sqrt{\mathrm{2}\pi}}\:\int_{−\infty} ^{+\infty} \:\varphi\left({t}\right)\:{e}^{−{ixt}} \:{dt} \\ $$ $$=\frac{\mathrm{1}}{\sqrt{\mathrm{2}\pi}}\:\int_{−{a}} ^{{a}} \:\:\:\frac{{e}^{−{ixt}} }{\sqrt{{a}^{\mathrm{2}} \:−{t}^{\mathrm{2}} }}\:{dt} \\ $$ $$=\sqrt{\frac{\mathrm{2}}{\pi}}\:\:\int_{\mathrm{0}} ^{{a}} \:\:\:\frac{{cos}\left({xt}\right)}{\sqrt{{a}^{\mathrm{2}} \:−{t}^{\mathrm{2}} }}{dt}\:\:\:{let}\:{find}\: \\ $$ $${w}\left({x}\right)\:=\int_{\mathrm{0}} ^{{a}} \:\:\:\:\:\:\frac{{cos}\left({xt}\right)}{\sqrt{{a}^{\mathrm{2}} \:−{t}^{\mathrm{2}} }}{dt}\:{we}\:{hsve} \\ $$ $${w}^{'} \left({x}\right)\:=\:\int_{\mathrm{0}} ^{{a}} \:\:\frac{−{t}\:{sin}\left({xt}\right)}{\sqrt{{a}^{\mathrm{2}} \:−{t}^{\mathrm{2}} }}\:\:\:{and}\:{by}\:{parts} \\ $$ $${w}^{'} \left({x}\right)\:\:=\:\left[\:\sqrt{{a}^{\mathrm{2}} \:−{t}^{\mathrm{2}} }\:{sin}\left({xt}\right)\right]_{\mathrm{0}} ^{{a}} \:−\int_{\mathrm{0}} ^{{a}} \:\sqrt{{a}^{\mathrm{2}} \:−{t}^{\mathrm{2}} }\:{x}\:{cos}\left({xt}\right){dt} \\ $$ $$=\:−{x}\:\int_{\mathrm{0}} ^{{a}} \:\:\sqrt{{a}^{\mathrm{2}} \:−{t}^{\mathrm{2}} \:}\:\:{cos}\left({xt}\right){dt}\:\:\:{chsngement}\:{t}\:={asin}\alpha \\ $$ $${give}\:{w}^{'} \left({x}\right)\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:{a}\:{cos}\left(\alpha\right){cos}\left({ax}\:{sin}\alpha\right)\:{a}\:{cos}\alpha\:{d}\alpha \\ $$ $$=\:{a}^{\mathrm{2}} \:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:{cos}^{\mathrm{2}} \left(\alpha\right)\:{cos}\left({ax}\:{sin}\alpha\right){d}\alpha \\ $$ $$={a}^{\mathrm{2}} \:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}\left(\alpha\right)\:\left({cos}\left(\alpha\right)\:{cos}\left({ax}\:{sin}\alpha\right)\right){d}\alpha \\ $$ $$={a}^{\mathrm{2}} \:\:\left\{\:\frac{\mathrm{1}}{{ax}}\:{sin}\left({ax}\:{sin}\left(\alpha\right)\right){cos}\left(\alpha\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$ $$\left.−\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:−{sin}\left(\alpha\right)\:{sin}\left({ax}\:{sin}\alpha\right)\:{d}\alpha\right\} \\ $$ $$=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:{sin}\left(\alpha\right)\:{sin}\left({ax}\:{sin}\alpha\right){d}\alpha\:....{be}\:{continued}... \\ $$
