Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 35689 by prof Abdo imad last updated on 22/May/18

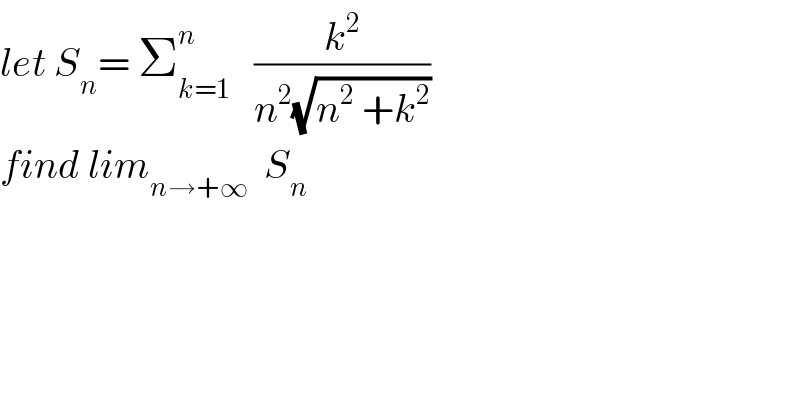
let S_n = Σ_(k=1) ^n (k^2 /(n^2 (√(n^2 +k^2 )))) find lim_(n→+∞) S_n

$${let}\:{S}_{{n}} =\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\:\frac{{k}^{\mathrm{2}} }{{n}^{\mathrm{2}} \sqrt{{n}^{\mathrm{2}} \:+{k}^{\mathrm{2}} }} \\ $$$${find}\:{lim}_{{n}\rightarrow+\infty} \:\:{S}_{{n}} \\ $$

Commented by prof Abdo imad last updated on 22/May/18

we have S_n = Σ_(k=1) ^n (k^2 /(n^3 (√(1+(k^2 /n^2 ))))) = (1/n) Σ_(k=1) ^n ((k^2 /n^2 )/(√(1+(k^2 /n^2 )))) so S_n is a Rieman sum and lim_(n→+∞) S_n = ∫_0 ^1 (x^2 /(√(1+x^2 )))dx =I changement x =sht give t=argsh(x) and I = ∫_0 ^(ln(1+(√2))) ((sh^2 t)/(cht)) ch tdt = ∫_0 ^(ln(1+(√2))) sh^2 t dt =(1/2) ∫_0 ^(ln(1+(√2))) (ch(2t)−1)dt =(1/2) ∫_0 ^(ln(1+(√2))) ch(2t) dt −((ln(1+(√2)))/2) =(1/4)[ sh(2t)]_0 ^(ln(1+(√2))) − ((ln(1+(√2)))/2) =(1/4)sh(2ln(1+(√2))) −((ln(1+(√2)))/2) sh(2x)= ((e^(2x) −e^(−2x) )/2) ⇒ sh(2x)=(((1+(√2))^4 +(1/((1+(√2))^2 )))/2) I = (1/8){ (1+(√2))^4 −(1+(√2))^(−4) } −((ln(1+(√2)})/2)

$${we}\:{have}\:{S}_{{n}} \:=\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\:\frac{{k}^{\mathrm{2}} }{{n}^{\mathrm{3}} \sqrt{\mathrm{1}+\frac{{k}^{\mathrm{2}} }{{n}^{\mathrm{2}} }}} \\ $$$$=\:\frac{\mathrm{1}}{{n}}\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\frac{\frac{{k}^{\mathrm{2}} }{{n}^{\mathrm{2}} }}{\sqrt{\mathrm{1}+\frac{{k}^{\mathrm{2}} }{{n}^{\mathrm{2}} }}}\:{so}\:{S}_{{n}} \:{is}\:{a}\:{Rieman}\:{sum} \\ $$$${and}\:{lim}_{{n}\rightarrow+\infty} \:\:{S}_{{n}} \:\:=\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{x}^{\mathrm{2}} }{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{dx}\:={I} \\ $$$${changement}\:\:{x}\:={sht}\:{give}\:{t}={argsh}\left({x}\right)\:{and} \\ $$$${I}\:\:=\:\int_{\mathrm{0}} ^{{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} \:\:\frac{{sh}^{\mathrm{2}} {t}}{{cht}}\:{ch}\:{tdt}\:=\:\int_{\mathrm{0}} ^{{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} \:{sh}^{\mathrm{2}} {t}\:{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} \:\:\left({ch}\left(\mathrm{2}{t}\right)−\mathrm{1}\right){dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} {ch}\left(\mathrm{2}{t}\right)\:{dt}\:\:\:−\frac{{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)}{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left[\:{sh}\left(\mathrm{2}{t}\right)\right]_{\mathrm{0}} ^{{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} \:−\:\frac{{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)}{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}{sh}\left(\mathrm{2}{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\right)\:−\frac{{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)}{\mathrm{2}} \\ $$$${sh}\left(\mathrm{2}{x}\right)=\:\frac{{e}^{\mathrm{2}{x}} \:−{e}^{−\mathrm{2}{x}} }{\mathrm{2}}\:\Rightarrow\:{sh}\left(\mathrm{2}{x}\right)=\frac{\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\mathrm{4}} \:+\frac{\mathrm{1}}{\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\mathrm{2}} }}{\mathrm{2}} \\ $$$${I}\:=\:\frac{\mathrm{1}}{\mathrm{8}}\left\{\:\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\mathrm{4}} \:−\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{−\mathrm{4}} \right\}\:−\frac{{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right\}}{\mathrm{2}} \\ $$

Commented by prof Abdo imad last updated on 22/May/18

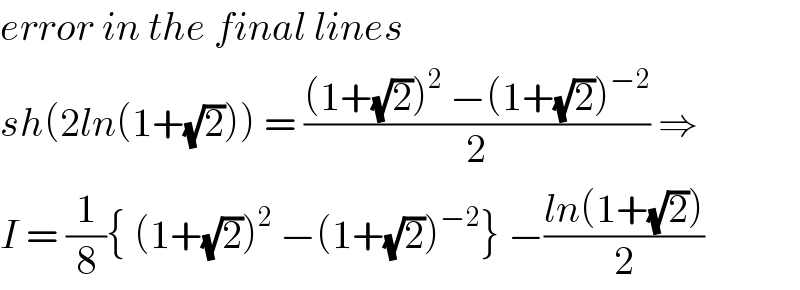
error in the final lines sh(2ln(1+(√2))) = (((1+(√2))^2 −(1+(√2))^(−2) )/2) ⇒ I = (1/8){ (1+(√2))^2 −(1+(√2))^(−2) } −((ln(1+(√2)))/2)

$${error}\:{in}\:{the}\:{final}\:{lines} \\ $$$${sh}\left(\mathrm{2}{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\right)\:=\:\frac{\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\mathrm{2}} \:−\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{−\mathrm{2}} }{\mathrm{2}}\:\Rightarrow \\ $$$${I}\:=\:\frac{\mathrm{1}}{\mathrm{8}}\left\{\:\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\mathrm{2}} \:−\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{−\mathrm{2}} \right\}\:−\frac{{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)}{\mathrm{2}} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 22/May/18

=((lim)/(n→∞))×(1/n)×((((k/n))^2 )/(√(1+((k/n))^2 ))) =∫_0 ^1 (x^2 /((√(1+x^2 )) ))dx =∫_0 ^1 (√(1+x^2 )) dx−∫_0 ^1 (dx/(√(1+x^2 ))) now use formula

$$=\frac{{lim}}{{n}\rightarrow\infty}×\frac{\mathrm{1}}{{n}}×\frac{\left(\frac{{k}}{{n}}\right)^{\mathrm{2}} }{\sqrt{\mathrm{1}+\left(\frac{{k}}{{n}}\right)^{\mathrm{2}} }} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{2}} }{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:\:\:{dx}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }} \\ $$$${now}\:{use}\:{formula} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com