Question and Answers Forum
Question Number 35821 by prof Abdo imad last updated on 24/May/18
Commented byprof Abdo imad last updated on 31/May/18
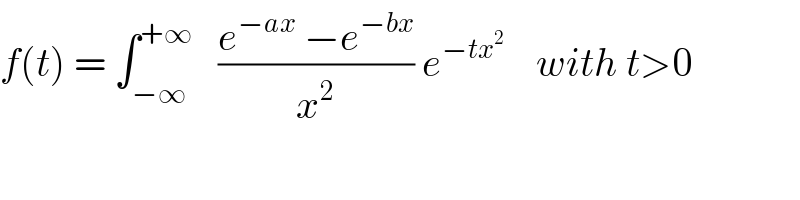
Commented byprof Abdo imad last updated on 31/May/18
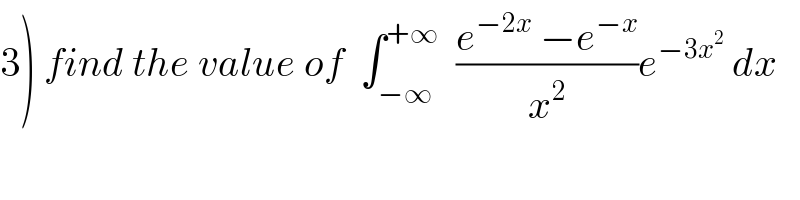
Commented byabdo mathsup 649 cc last updated on 01/Jun/18

Commented byabdo mathsup 649 cc last updated on 01/Jun/18