Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 35832 by abdo mathsup 649 cc last updated on 24/May/18

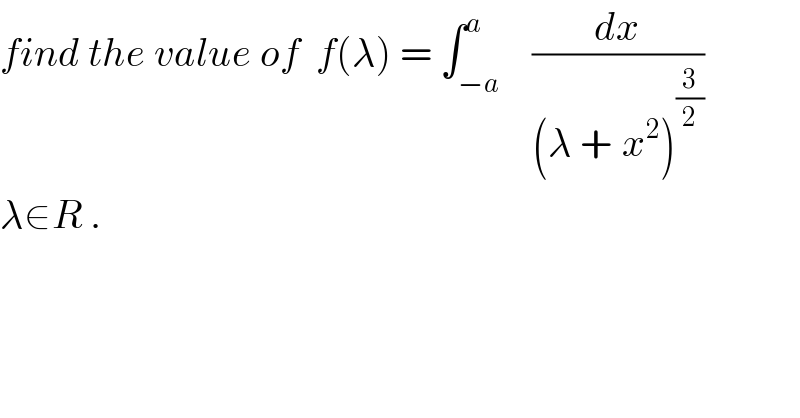
find the value of f(λ) = ∫_(−a) ^a (dx/((λ +_ x^2 )^(3/2) )) λ∈R .

$${find}\:{the}\:{value}\:{of}\:\:{f}\left(\lambda\right)\:=\:\int_{−{a}} ^{{a}} \:\:\:\frac{{dx}}{\left(\lambda\:+_{} {x}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$$$\lambda\in{R}\:. \\ $$

Commented by abdo.msup.com last updated on 25/May/18

case 1 ifλ>0 let use the changement x=(√λ) tan(t) f(λ) = ∫_(−arctan((a/λ))) ^(arctan((a/λ))) ((√λ)/(λ^(3/2) (1+tan^2 (t))^(3/2) )) (1+tan^2 t)dt =(1/λ)∫_(−arctan((a/(√λ)))) ^(arctan( (a/(√λ))) ) (1/((1+tan^2 t)^(1/2) ))dt = (2/λ) ∫_0 ^(arctan((a/(√λ)))) cos(t) dt =(2/λ) [ sin(t)]_0 ^(arctan((a/(√λ)))) = (2/λ) sin(arctan((a/(√λ)))) but we have sin(arctanx) = (x/(√(1+x^2 ))) so sin(arctan((a/(√λ)))) = (a/((√λ) (√(1+(a^2 /λ))))) = (a/(√(λ +a^2 ))) ⇒f(λ) = ((2a)/(λ(√(λ+a^2 ))))

$${case}\:\mathrm{1}\:{if}\lambda>\mathrm{0}\:{let}\:{use}\:{the}\:{changement} \\ $$$${x}=\sqrt{\lambda}\:{tan}\left({t}\right) \\ $$$${f}\left(\lambda\right)\:=\:\int_{−{arctan}\left(\frac{{a}}{\lambda}\right)} ^{{arctan}\left(\frac{{a}}{\lambda}\right)} \:\:\:\frac{\sqrt{\lambda}}{\lambda^{\frac{\mathrm{3}}{\mathrm{2}}} \left(\mathrm{1}+{tan}^{\mathrm{2}} \left({t}\right)\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }\:\left(\mathrm{1}+{tan}^{\mathrm{2}} {t}\right){dt} \\ $$$$=\frac{\mathrm{1}}{\lambda}\int_{−{arctan}\left(\frac{{a}}{\sqrt{\lambda}}\right)} ^{{arctan}\left(\:\frac{{a}}{\sqrt{\lambda}}\right)\:} \:\:\:\frac{\mathrm{1}}{\left(\mathrm{1}+{tan}^{\mathrm{2}} {t}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} }{dt} \\ $$$$=\:\frac{\mathrm{2}}{\lambda}\:\int_{\mathrm{0}} ^{{arctan}\left(\frac{{a}}{\sqrt{\lambda}}\right)} \:\:{cos}\left({t}\right)\:{dt} \\ $$$$=\frac{\mathrm{2}}{\lambda}\:\left[\:{sin}\left({t}\right)\right]_{\mathrm{0}} ^{{arctan}\left(\frac{{a}}{\sqrt{\lambda}}\right)} \\ $$$$=\:\frac{\mathrm{2}}{\lambda}\:{sin}\left({arctan}\left(\frac{{a}}{\sqrt{\lambda}}\right)\right) \\ $$$${but}\:{we}\:{have}\:{sin}\left({arctanx}\right)\:=\:\frac{{x}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }} \\ $$$${so}\:{sin}\left({arctan}\left(\frac{{a}}{\sqrt{\lambda}}\right)\right)\:=\:\frac{{a}}{\sqrt{\lambda}\:\sqrt{\mathrm{1}+\frac{{a}^{\mathrm{2}} }{\lambda}}} \\ $$$$=\:\frac{{a}}{\sqrt{\lambda\:+{a}^{\mathrm{2}} }}\:\Rightarrow{f}\left(\lambda\right)\:=\:\frac{\mathrm{2}{a}}{\lambda\sqrt{\lambda+{a}^{\mathrm{2}} }} \\ $$

Commented by prof Abdo imad last updated on 25/May/18

case 2 if λ<0 ⇒ −λ >0 let put α =−λ f(λ) = ∫_(−a) ^a (dx/((x^2 −α)^(3/2) )) .changement x=(√α)ch(t) give f(λ) = ∫_(argch( ((−a)/(√α)))) ^(argch( (a/(√α)))) (((√α) sh(t))/(α^(3/2) ( ch^2 (t)−1)^(3/2) ))dt = (1/α)∫_(argch(((−a)/(√α)))) ^(argch( (a/(√α)))) ((sh(t))/(sh^3 (t)))dt = (2/α) ∫_(argch( ((−a)/(√α)))) ^(argch((a/(√α)))) (dt/(ch(2t)−1)) = (2/α) ∫_(ln( −(a/(√κ)) +(√( (a^2 /α) −1)))) ^(ln( (a/(√α)) +(√( (a^2 /α)−1))) (dt/(((e^(2t) +e^(−2t) )/2) −1)) = (4/α) ∫_(ln(−(a/(√α)) +(√( (a^2 /α)−1)))) ^(ln( (a/(√α)) +(√((a^2 /α)−1)))) (dt/(e^(2t) +e^(−2t) −2)) ... be continued...

$${case}\:\mathrm{2}\:{if}\:\:\lambda<\mathrm{0}\:\Rightarrow\:−\lambda\:>\mathrm{0}\:{let}\:{put}\:\alpha\:=−\lambda \\ $$$${f}\left(\lambda\right)\:=\:\int_{−{a}} ^{{a}} \:\:\:\frac{{dx}}{\left({x}^{\mathrm{2}} \:−\alpha\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }\:\:.{changement}\:{x}=\sqrt{\alpha}{ch}\left({t}\right) \\ $$$${give}\: \\ $$$${f}\left(\lambda\right)\:=\:\int_{{argch}\left(\:\frac{−{a}}{\sqrt{\alpha}}\right)} ^{{argch}\left(\:\frac{{a}}{\sqrt{\alpha}}\right)} \:\:\:\:\:\frac{\sqrt{\alpha}\:\:{sh}\left({t}\right)}{\alpha^{\frac{\mathrm{3}}{\mathrm{2}}} \left(\:{ch}^{\mathrm{2}} \left({t}\right)−\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{dt} \\ $$$$=\:\frac{\mathrm{1}}{\alpha}\int_{{argch}\left(\frac{−{a}}{\sqrt{\alpha}}\right)} ^{{argch}\left(\:\frac{{a}}{\sqrt{\alpha}}\right)} \:\:\:\:\frac{{sh}\left({t}\right)}{{sh}^{\mathrm{3}} \left({t}\right)}{dt}\: \\ $$$$=\:\frac{\mathrm{2}}{\alpha}\:\int_{{argch}\left(\:\frac{−{a}}{\sqrt{\alpha}}\right)} ^{{argch}\left(\frac{{a}}{\sqrt{\alpha}}\right)} \:\:\:\:\:\frac{{dt}}{{ch}\left(\mathrm{2}{t}\right)−\mathrm{1}} \\ $$$$=\:\frac{\mathrm{2}}{\alpha}\:\int_{{ln}\left(\:−\frac{{a}}{\sqrt{\kappa}}\:\:+\sqrt{\:\frac{{a}^{\mathrm{2}} }{\alpha}\:−\mathrm{1}}\right)} ^{{ln}\left(\:\frac{{a}}{\sqrt{\alpha}}\:+\sqrt{\:\frac{{a}^{\mathrm{2}} }{\alpha}−\mathrm{1}}\right.} \:\:\:\:\:\:\:\frac{{dt}}{\frac{{e}^{\mathrm{2}{t}} \:+{e}^{−\mathrm{2}{t}} }{\mathrm{2}}\:−\mathrm{1}} \\ $$$$=\:\frac{\mathrm{4}}{\alpha}\:\int_{{ln}\left(−\frac{{a}}{\sqrt{\alpha}}\:+\sqrt{\:\frac{{a}^{\mathrm{2}} }{\alpha}−\mathrm{1}}\right)} ^{{ln}\left(\:\frac{{a}}{\sqrt{\alpha}}\:+\sqrt{\frac{{a}^{\mathrm{2}} }{\alpha}−\mathrm{1}}\right)} \:\:\:\:\:\frac{{dt}}{{e}^{\mathrm{2}{t}} \:+{e}^{−\mathrm{2}{t}} \:−\mathrm{2}}\:... \\ $$$${be}\:{continued}... \\ $$$$ \\ $$

Commented by prof Abdo imad last updated on 26/May/18

let find K=∫ (dt/(e^(2t) +e^(−2t) −2)) chamgement e^(2t) =u give K = ∫ (1/(u +u^(−1) −2)) (du/(2u)) =(1/2) ∫ (du/(u^2 +1 −2u)) =(1/2)∫ (du/((u−1)^2 )) = −(1/(2(u−1))) =((−1)/(2(e^(2t) −1))) +c so f(λ) = −(4/(2α)) [ (1/(e^(2t) −1))]_(ln(((−a)/(√α)) +(√((a^2 /α)−1))) ^(ln( (a/(√α)) +(√((a^2 /α) −1))) = ((−2)/α){ (1/(((a/(√α)) +(√((a^2 /α)−1))))) − (1/((−(a/(√α))+(√((a^2 /α) −1))))) = (2/λ){ (1/(( (a/(√(−λ))) +(√(−(a^2 /λ)−1)))))−(1/((((−a)/(√(−λ)))+(√(−(a^2 /λ)−1))))) with λ<0 .

$${let}\:{find}\:{K}=\int\:\:\:\:\:\:\:\frac{{dt}}{{e}^{\mathrm{2}{t}} \:+{e}^{−\mathrm{2}{t}} \:−\mathrm{2}}\:\:{chamgement} \\ $$$${e}^{\mathrm{2}{t}} \:={u}\:{give}\:\:{K}\:=\:\int\:\:\frac{\mathrm{1}}{{u}\:+{u}^{−\mathrm{1}} \:−\mathrm{2}}\:\frac{{du}}{\mathrm{2}{u}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\:\:\:\:\:\frac{{du}}{{u}^{\mathrm{2}} \:+\mathrm{1}\:−\mathrm{2}{u}}\:=\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\:\frac{{du}}{\left({u}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\:−\frac{\mathrm{1}}{\mathrm{2}\left({u}−\mathrm{1}\right)}\:\:=\frac{−\mathrm{1}}{\mathrm{2}\left({e}^{\mathrm{2}{t}} \:−\mathrm{1}\right)}\:+{c}\:{so} \\ $$$${f}\left(\lambda\right)\:=\:−\frac{\mathrm{4}}{\mathrm{2}\alpha}\:\left[\:\:\frac{\mathrm{1}}{{e}^{\mathrm{2}{t}} −\mathrm{1}}\right]_{{ln}\left(\frac{−{a}}{\sqrt{\alpha}}\:+\sqrt{\frac{{a}^{\mathrm{2}} }{\alpha}−\mathrm{1}}\right.} ^{{ln}\left(\:\frac{{a}}{\sqrt{\alpha}}\:+\sqrt{\frac{{a}^{\mathrm{2}} }{\alpha}\:−\mathrm{1}}\right.} \\ $$$$=\:\frac{−\mathrm{2}}{\alpha}\left\{\:\:\:\:\:\frac{\mathrm{1}}{\left(\frac{{a}}{\sqrt{\alpha}}\:+\sqrt{\frac{{a}^{\mathrm{2}} }{\alpha}−\mathrm{1}}\right)}\:−\:\frac{\mathrm{1}}{\left(−\frac{{a}}{\sqrt{\alpha}}+\sqrt{\frac{{a}^{\mathrm{2}} }{\alpha}\:−\mathrm{1}}\right)}\right. \\ $$$$=\:\frac{\mathrm{2}}{\lambda}\left\{\:\:\:\:\:\frac{\mathrm{1}}{\left(\:\frac{{a}}{\sqrt{−\lambda}}\:+\sqrt{−\frac{{a}^{\mathrm{2}} }{\lambda}−\mathrm{1}}\right)}−\frac{\mathrm{1}}{\left(\frac{−{a}}{\sqrt{−\lambda}}+\sqrt{−\frac{{a}^{\mathrm{2}} }{\lambda}−\mathrm{1}}\right)}\right. \\ $$$${with}\:\lambda<\mathrm{0}\:. \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 24/May/18

x=(√λ) tanθ dx=(√λ) sec^2 θ dθ I=∫(((√λ) sec^2 θ dθ)/({λ(1+tan^2 θ)}^(3/2) )) ∫(1/λ) ×((sec^2 θ)/(sec^3 θ))×(dθ/) =(1/λ)∫cosθ dθ =(1/λ)sinθ now putting the limit =(1/λ)×∣(x/((λ+x^2 )^(1/2) ))∣_(−a) ^a =(1/λ)×((2a)/((λ+a^2 )^(1/2) ))

$${x}=\sqrt{\lambda}\:{tan}\theta\:\:\:{dx}=\sqrt{\lambda}\:{sec}^{\mathrm{2}} \theta\:{d}\theta \\ $$$${I}=\int\frac{\sqrt{\lambda}\:{sec}^{\mathrm{2}} \theta\:{d}\theta}{\left\{\lambda\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right)\right\}^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$$$\int\frac{\mathrm{1}}{\lambda}\:×\frac{{sec}^{\mathrm{2}} \theta}{{sec}^{\mathrm{3}} \theta}×\frac{{d}\theta}{} \\ $$$$=\frac{\mathrm{1}}{\lambda}\int{cos}\theta\:{d}\theta \\ $$$$=\frac{\mathrm{1}}{\lambda}{sin}\theta\:\:{now}\:{putting}\:{the}\:{limit} \\ $$$$=\frac{\mathrm{1}}{\lambda}×\mid\frac{{x}}{\left(\lambda+{x}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} \:}\mid_{−{a}} ^{{a}} \\ $$$$=\frac{\mathrm{1}}{\lambda}×\frac{\mathrm{2}{a}}{\left(\lambda+{a}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} } \\ $$

Commented by abdo.msup.com last updated on 25/May/18

your answer is correct sir Tanmay but you must study the case λ<0....

$${your}\:{answer}\:{is}\:{correct}\:{sir}\:{Tanmay} \\ $$$${but}\:{you}\:{must}\:{study}\:{the}\:{case}\:\lambda<\mathrm{0}.... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com