Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 3584 by prakash jain last updated on 16/Dec/15

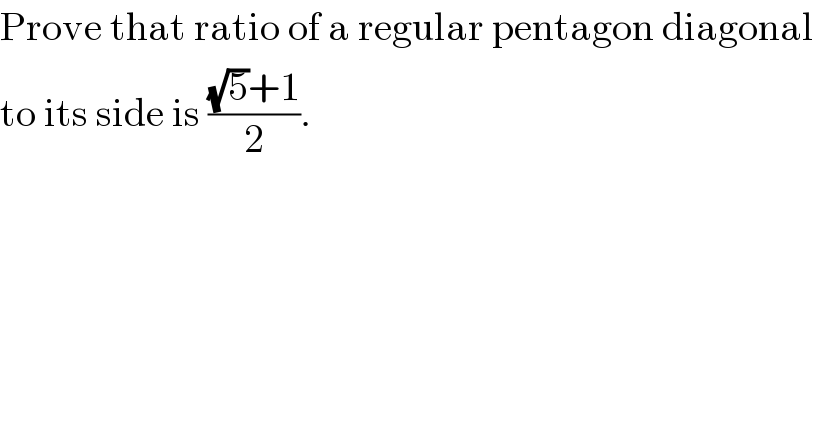
Prove that ratio of a regular pentagon diagonal to its side is (((√5)+1)/2).

$$\mathrm{Prove}\:\mathrm{that}\:\mathrm{ratio}\:\mathrm{of}\:\mathrm{a}\:\mathrm{regular}\:\mathrm{pentagon}\:\mathrm{diagonal} \\ $$$$\mathrm{to}\:\mathrm{its}\:\mathrm{side}\:\mathrm{is}\:\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}}. \\ $$

Commented by Yozzii last updated on 15/Dec/15

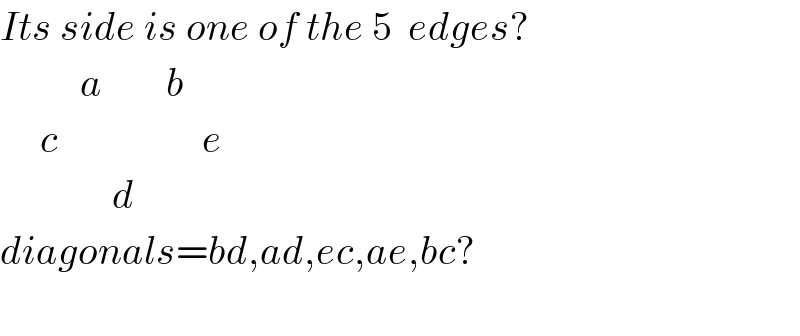
Its side is one of the 5 edges? a b c e d diagonals=bd,ad,ec,ae,bc?

$${Its}\:{side}\:{is}\:{one}\:{of}\:{the}\:\mathrm{5}\:\:{edges}? \\ $$$$\:\:\:\:\:\:\:\:\:\:{a}\:\:\:\:\:\:\:\:{b} \\ $$$$\:\:\:\:\:{c}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{e} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:{d} \\ $$$${diagonals}={bd},{ad},{ec},{ae},{bc}? \\ $$$$ \\ $$

Commented by prakash jain last updated on 15/Dec/15

yes. Also it (((√5)+1)/2)

$${yes}.\:\mathrm{Also}\:\mathrm{it}\:\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}} \\ $$

Commented by Yozzii last updated on 16/Dec/15

Could a general formula for the value of such a ratio be found in terms of n for a regular n−gon?

$${Could}\:{a}\:{general}\:{formula}\:{for}\:{the} \\ $$$${value}\:{of}\:{such}\:{a}\:{ratio}\:{be}\:{found}\:{in}\:{terms} \\ $$$${of}\:{n}\:{for}\:{a}\:{regular}\:{n}−{gon}? \\ $$

Commented by prakash jain last updated on 16/Dec/15

A formula using sin function is clear. A general algebria formula will require solving n^(th) root of unity as an algebric formula.

$$\mathrm{A}\:\mathrm{formula}\:\mathrm{using}\:\mathrm{sin}\:\mathrm{function}\:\mathrm{is}\:\mathrm{clear}.\: \\ $$$$\mathrm{A}\:\mathrm{general}\:\mathrm{algebria}\:\mathrm{formula}\:\mathrm{will}\:\mathrm{require}\:\mathrm{solving} \\ $$$${n}^{{th}} \:\mathrm{root}\:\mathrm{of}\:\mathrm{unity}\:\mathrm{as}\:\mathrm{an}\:\mathrm{algebric}\:\mathrm{formula}. \\ $$

Commented by Rasheed Soomro last updated on 16/Dec/15

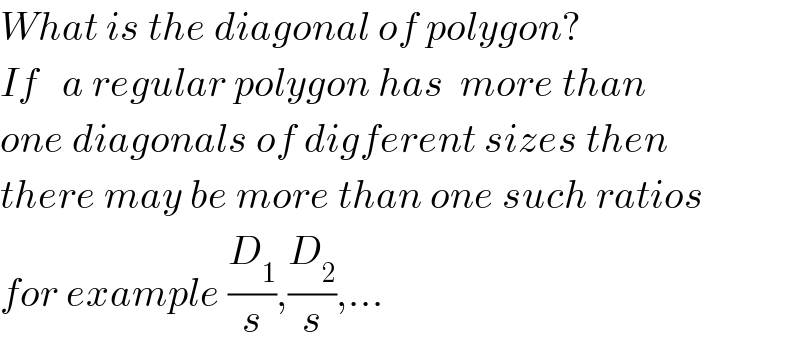
What is the diagonal of polygon? If a regular polygon has more than one diagonals of digferent sizes then there may be more than one such ratios for example (D_1 /s),(D_2 /s),...

$${What}\:{is}\:{the}\:{diagonal}\:{of}\:{polygon}? \\ $$$${If}\:\:\:{a}\:{regular}\:{polygon}\:{has}\:\:{more}\:{than}\: \\ $$$${one}\:{diagonals}\:{of}\:{digferent}\:{sizes}\:{then} \\ $$$${there}\:{may}\:{be}\:{more}\:{than}\:{one}\:{such}\:{ratios} \\ $$$${for}\:{example}\:\frac{{D}_{\mathrm{1}} }{{s}},\frac{{D}_{\mathrm{2}} }{{s}},... \\ $$

Commented by prakash jain last updated on 16/Dec/15

Yes. There will diagonals of different length.

$$\mathrm{Yes}.\:\mathrm{There}\:\mathrm{will}\:\mathrm{diagonals}\:\mathrm{of}\:\mathrm{different}\:\mathrm{length}. \\ $$

Answered by Yozzii last updated on 16/Dec/15

All regular n−gons can be inscribed in a circle. PROOF: Consider the n roots of the equation z^n =re^(iθ) where i=(√(−1)),r>0,n∈N+{0},−π<θ≤π. Since e^(iθ) =e^(i(θ+2πt)) (t∈Z), because of the periodicity of the sine and cosine functions which arise from the form e^(iθ) =cosθ+isinθ, ⇒ z^n =re^(i(θ+2tπ)) ⇒z=r^(1/n) e^(i((θ+2tπ)/n)) . The n values of z are obtained for 0≤t≤n−1. Observe that each value of z has the common modulus r^(1/n) . On an Argand diagram, say the n values of z are plotted with lines joining their points to the origin. Suppose one point has argument α_t =((θ+2tπ)/n) and an adjacent point has argument α_(t+1) =((θ+2(t+1)π)/n). ⇒ α_(t+1) −α_t =((θ+2tπ+2π−θ−2tπ)/n)=((2π)/n). The angle between the lines joining consecutive points is a constant (((2π)/n)) independent of t and all of these n angular differences sum to 2π. Thus, the n points are regularly positioned about the origin and they may be joined by lines to form a regular n−gon figure. These n points are placed about the origin and they are at the equal distances (r^(1/n) ) from the origin. These points hence, by definition of a circle as the locus of points at a fixed distance from a fixef point, lie on a circle. Since these n points form the corners of a regular n−gon, it follows that such a figure can be inscribed in a circle. □ So, inscribe a pentagon ABCDE in a circle and let its radius be denoted by r. The angle at the centre O of the pentagon in each of the five sectors is ((2π)/5)≡72°. Denote s as the side length of the pentagon. Draw a perpendicular bisector of one side of the pentagon (e.g AB). In so doing, one of the sectors is symmetrically bisected to form two right−angled triangles, with hypothenuses being the radius r of the circle, and s is halved.

$${All}\:{regular}\:{n}−{gons}\:{can}\:{be}\:{inscribed} \\ $$$${in}\:{a}\:{circle}. \\ $$$$\mathrm{PROOF}: \\ $$$${Consider}\:{the}\:{n}\:{roots}\:{of}\:{the}\:{equation} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{z}^{{n}} ={re}^{{i}\theta} \: \\ $$$${where}\:{i}=\sqrt{−\mathrm{1}},{r}>\mathrm{0},{n}\in\mathbb{N}+\left\{\mathrm{0}\right\},−\pi<\theta\leqslant\pi. \\ $$$${Since}\:{e}^{{i}\theta} ={e}^{{i}\left(\theta+\mathrm{2}\pi{t}\right)} \:\left({t}\in\mathbb{Z}\right),\:{because}\:{of}\:{the}\:{periodicity} \\ $$$${of}\:{the}\:{sine}\:{and}\:{cosine}\:{functions}\:{which} \\ $$$${arise}\:{from}\:{the}\:{form}\:{e}^{{i}\theta} ={cos}\theta+{isin}\theta, \\ $$$$\Rightarrow\:{z}^{{n}} ={re}^{{i}\left(\theta+\mathrm{2}{t}\pi\right)} \Rightarrow{z}={r}^{\mathrm{1}/{n}} {e}^{{i}\frac{\theta+\mathrm{2}{t}\pi}{{n}}} . \\ $$$$ \\ $$$${The}\:{n}\:{values}\:{of}\:{z}\:{are}\:{obtained}\:{for}\:\mathrm{0}\leqslant{t}\leqslant{n}−\mathrm{1}. \\ $$$${Observe}\:{that}\:{each}\:{value}\:{of}\:{z}\:{has}\:{the} \\ $$$${common}\:{modulus}\:{r}^{\mathrm{1}/{n}} .\:{On}\:{an}\:{Argand} \\ $$$${diagram},\:{say}\:{the}\:{n}\:{values}\:{of}\:{z}\:{are}\:{plotted} \\ $$$${with}\:{lines}\:{joining}\:{their}\:{points}\:{to}\:{the} \\ $$$${origin}.\:{Suppose}\:{one}\:{point}\:{has}\:{argument} \\ $$$$\alpha_{{t}} =\frac{\theta+\mathrm{2}{t}\pi}{{n}}\:{and}\:{an}\:{adjacent}\:{point}\:{has}\: \\ $$$${argument}\:\alpha_{{t}+\mathrm{1}} =\frac{\theta+\mathrm{2}\left({t}+\mathrm{1}\right)\pi}{{n}}. \\ $$$$\Rightarrow\:\alpha_{{t}+\mathrm{1}} −\alpha_{{t}} =\frac{\theta+\mathrm{2}{t}\pi+\mathrm{2}\pi−\theta−\mathrm{2}{t}\pi}{{n}}=\frac{\mathrm{2}\pi}{{n}}. \\ $$$${The}\:{angle}\:{between}\:{the}\:{lines}\:{joining} \\ $$$${consecutive}\:{points}\:{is}\:{a}\:{constant}\:\left(\frac{\mathrm{2}\pi}{{n}}\right) \\ $$$${independent}\:{of}\:{t}\:{and}\:{all}\:{of}\:{these}\:{n} \\ $$$${angular}\:{differences}\:{sum}\:{to}\:\mathrm{2}\pi.\:{Thus},\:{the} \\ $$$${n}\:{points}\:{are}\:{regularly}\:{positioned}\:{about}\:{the} \\ $$$${origin}\:{and}\:{they}\:{may}\:{be}\:{joined}\:{by}\:{lines} \\ $$$${to}\:{form}\:{a}\:{regular}\:{n}−{gon}\:{figure}. \\ $$$${These}\:{n}\:{points}\:{are}\:{placed}\:{about}\:{the}\: \\ $$$${origin}\:{and}\:{they}\:{are}\:{at}\:{the}\:{equal}\:{distances}\:\left({r}^{\mathrm{1}/{n}} \right) \\ $$$${from}\:{the}\:{origin}.\:{These}\:{points}\:{hence}, \\ $$$${by}\:{definition}\:{of}\:{a}\:{circle}\:{as}\:{the}\:{locus}\:{of} \\ $$$${points}\:{at}\:{a}\:{fixed}\:{distance}\:{from}\:{a}\:{fixef} \\ $$$${point},\:{lie}\:{on}\:{a}\:{circle}.\:{Since}\:{these}\:{n}\:{points} \\ $$$${form}\:{the}\:{corners}\:{of}\:{a}\:{regular}\:{n}−{gon}, \\ $$$${it}\:{follows}\:{that}\:{such}\:{a}\:{figure}\:{can}\:{be} \\ $$$${inscribed}\:{in}\:{a}\:{circle}.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Box \\ $$$$ \\ $$$${So},\:{inscribe}\:{a}\:{pentagon}\:{ABCDE}\:{in}\:{a}\:{circle}\:{and} \\ $$$${let}\:{its}\:{radius}\:{be}\:{denoted}\:{by}\:{r}.\:{The} \\ $$$${angle}\:{at}\:{the}\:{centre}\:{O}\:{of}\:{the}\:{pentagon}\:{in} \\ $$$${each}\:{of}\:{the}\:{five}\:{sectors}\:{is}\:\frac{\mathrm{2}\pi}{\mathrm{5}}\equiv\mathrm{72}°. \\ $$$${Denote}\:{s}\:{as}\:{the}\:{side}\:{length}\:{of}\:{the}\:{pentagon}. \\ $$$${Draw}\:{a}\:{perpendicular}\:{bisector}\:{of}\:{one} \\ $$$${side}\:{of}\:{the}\:{pentagon}\:\left({e}.{g}\:{AB}\right).\:{In}\:{so}\:{doing},\:{one} \\ $$$${of}\:{the}\:{sectors}\:{is}\:{symmetrically}\:{bisected} \\ $$$${to}\:{form}\:{two}\:{right}−{angled}\:{triangles}, \\ $$$${with}\:{hypothenuses}\:{being}\:{the}\:{radius}\:{r}\:{of} \\ $$$${the}\:{circle},\:{and}\:{s}\:{is}\:{halved}.\: \\ $$$$ \\ $$

Commented by Yozzii last updated on 16/Dec/15

Thus, in such a triangle, (s/2)=rsin36^° ⇒r=(s/(2sin36°)) . (∗) Now, draw a line joining two points such that a diagonal D of the pentagon is obtained (e.g AC). Draw a perpendicular bisector of AC so that another right−angled triangle is obtained as before. However, the angle at O in this triangle is 72°. Therefore, we get (D/2)=rsin72^° ⇒r=(D/(2sin72°)) . (∗∗) Equating (∗) and (∗∗) we have (D/(2sin72^° ))=(s/(2sin36°))⇒(D/s)=((sin72^° )/(sin36°))=2cos36°.

$${Thus},\:{in}\:{such}\:{a}\:{triangle}, \\ $$$$\frac{{s}}{\mathrm{2}}={rsin}\mathrm{36}^{°} \Rightarrow{r}=\frac{{s}}{\mathrm{2}{sin}\mathrm{36}°}\:.\:\:\left(\ast\right) \\ $$$${Now},\:{draw}\:{a}\:{line}\:{joining}\:{two}\:{points} \\ $$$${such}\:{that}\:{a}\:{diagonal}\:{D}\:{of}\:{the}\:{pentagon} \\ $$$${is}\:{obtained}\:\left({e}.{g}\:{AC}\right).\:{Draw}\:{a}\:{perpendicular} \\ $$$${bisector}\:{of}\:{AC}\:{so}\:{that}\:{another}\:{right}−{angled} \\ $$$${triangle}\:{is}\:{obtained}\:{as}\:{before}.\:{However}, \\ $$$${the}\:{angle}\:{at}\:{O}\:{in}\:{this}\:{triangle}\:{is}\:\mathrm{72}°. \\ $$$${Therefore},\:{we}\:{get} \\ $$$$\frac{{D}}{\mathrm{2}}={rsin}\mathrm{72}^{°} \Rightarrow{r}=\frac{{D}}{\mathrm{2}{sin}\mathrm{72}°}\:.\:\left(\ast\ast\right) \\ $$$${Equating}\:\left(\ast\right)\:{and}\:\left(\ast\ast\right)\:{we}\:{have} \\ $$$$\frac{{D}}{\mathrm{2}{sin}\mathrm{72}^{°} }=\frac{{s}}{\mathrm{2}{sin}\mathrm{36}°}\Rightarrow\frac{{D}}{{s}}=\frac{{sin}\mathrm{72}^{°} }{{sin}\mathrm{36}°}=\mathrm{2}{cos}\mathrm{36}°. \\ $$$$ \\ $$

Commented by Yozzii last updated on 16/Dec/15

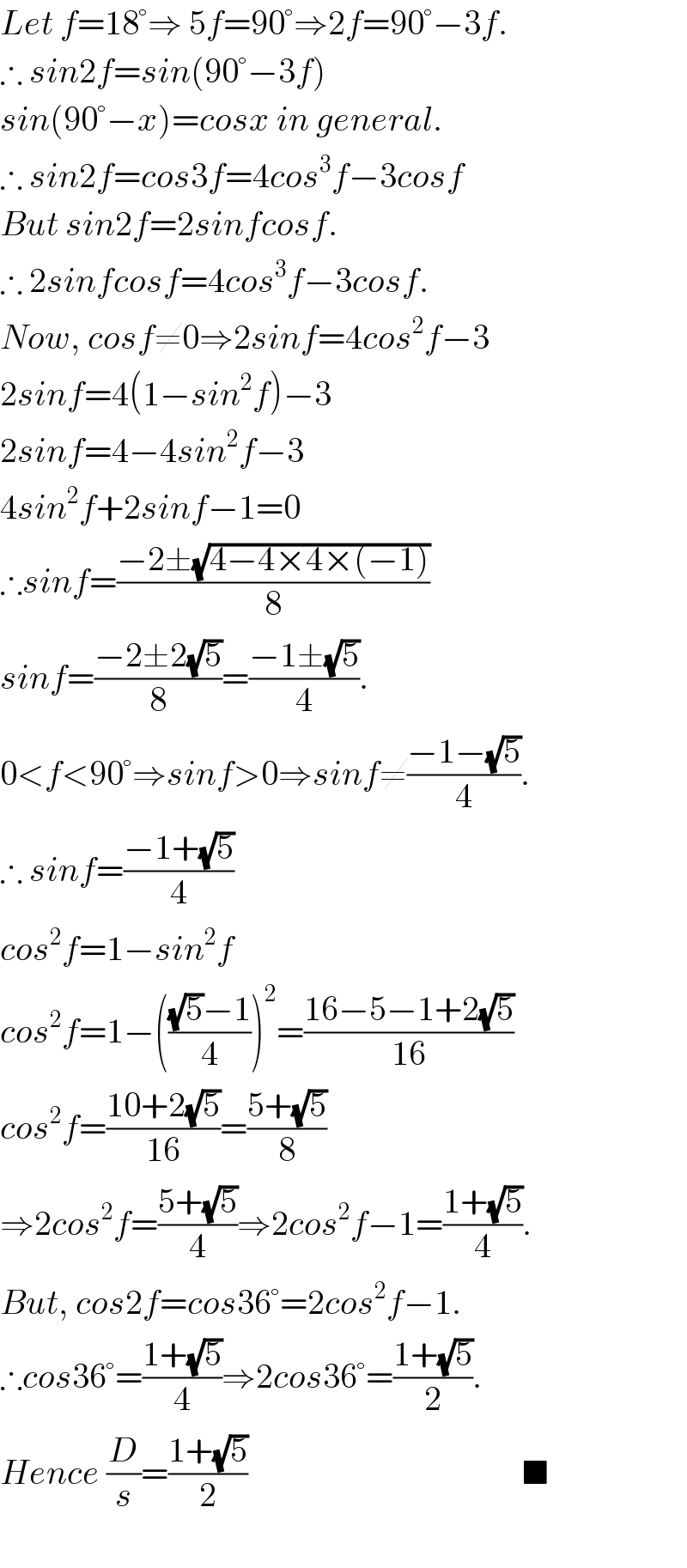
Let f=18°⇒ 5f=90°⇒2f=90°−3f. ∴ sin2f=sin(90°−3f) sin(90°−x)=cosx in general. ∴ sin2f=cos3f=4cos^3 f−3cosf But sin2f=2sinfcosf. ∴ 2sinfcosf=4cos^3 f−3cosf. Now, cosf≠0⇒2sinf=4cos^2 f−3 2sinf=4(1−sin^2 f)−3 2sinf=4−4sin^2 f−3 4sin^2 f+2sinf−1=0 ∴sinf=((−2±(√(4−4×4×(−1))))/8) sinf=((−2±2(√5))/8)=((−1±(√5))/4). 0<f<90°⇒sinf>0⇒sinf≠((−1−(√5))/4). ∴ sinf=((−1+(√5))/4) cos^2 f=1−sin^2 f cos^2 f=1−((((√5)−1)/4))^2 =((16−5−1+2(√5))/(16)) cos^2 f=((10+2(√5))/(16))=((5+(√5))/8) ⇒2cos^2 f=((5+(√5))/4)⇒2cos^2 f−1=((1+(√5))/4). But, cos2f=cos36°=2cos^2 f−1. ∴cos36°=((1+(√5))/4)⇒2cos36°=((1+(√5))/2). Hence (D/s)=((1+(√5))/2) ■

$${Let}\:{f}=\mathrm{18}°\Rightarrow\:\mathrm{5}{f}=\mathrm{90}°\Rightarrow\mathrm{2}{f}=\mathrm{90}°−\mathrm{3}{f}. \\ $$$$\therefore\:{sin}\mathrm{2}{f}={sin}\left(\mathrm{90}°−\mathrm{3}{f}\right) \\ $$$${sin}\left(\mathrm{90}°−{x}\right)={cosx}\:{in}\:{general}. \\ $$$$\therefore\:{sin}\mathrm{2}{f}={cos}\mathrm{3}{f}=\mathrm{4}{cos}^{\mathrm{3}} {f}−\mathrm{3}{cosf} \\ $$$${But}\:{sin}\mathrm{2}{f}=\mathrm{2}{sinfcosf}. \\ $$$$\therefore\:\mathrm{2}{sinfcosf}=\mathrm{4}{cos}^{\mathrm{3}} {f}−\mathrm{3}{cosf}. \\ $$$${Now},\:{cosf}\neq\mathrm{0}\Rightarrow\mathrm{2}{sinf}=\mathrm{4}{cos}^{\mathrm{2}} {f}−\mathrm{3} \\ $$$$\mathrm{2}{sinf}=\mathrm{4}\left(\mathrm{1}−{sin}^{\mathrm{2}} {f}\right)−\mathrm{3} \\ $$$$\mathrm{2}{sinf}=\mathrm{4}−\mathrm{4}{sin}^{\mathrm{2}} {f}−\mathrm{3} \\ $$$$\mathrm{4}{sin}^{\mathrm{2}} {f}+\mathrm{2}{sinf}−\mathrm{1}=\mathrm{0} \\ $$$$\therefore{sinf}=\frac{−\mathrm{2}\pm\sqrt{\mathrm{4}−\mathrm{4}×\mathrm{4}×\left(−\mathrm{1}\right)}}{\mathrm{8}} \\ $$$${sinf}=\frac{−\mathrm{2}\pm\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{8}}=\frac{−\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{4}}. \\ $$$$\mathrm{0}<{f}<\mathrm{90}°\Rightarrow{sinf}>\mathrm{0}\Rightarrow{sinf}\neq\frac{−\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{4}}. \\ $$$$\therefore\:{sinf}=\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}} \\ $$$${cos}^{\mathrm{2}} {f}=\mathrm{1}−{sin}^{\mathrm{2}} {f} \\ $$$${cos}^{\mathrm{2}} {f}=\mathrm{1}−\left(\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{2}} =\frac{\mathrm{16}−\mathrm{5}−\mathrm{1}+\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{16}} \\ $$$${cos}^{\mathrm{2}} {f}=\frac{\mathrm{10}+\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{16}}=\frac{\mathrm{5}+\sqrt{\mathrm{5}}}{\mathrm{8}} \\ $$$$\Rightarrow\mathrm{2}{cos}^{\mathrm{2}} {f}=\frac{\mathrm{5}+\sqrt{\mathrm{5}}}{\mathrm{4}}\Rightarrow\mathrm{2}{cos}^{\mathrm{2}} {f}−\mathrm{1}=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}}. \\ $$$${But},\:{cos}\mathrm{2}{f}={cos}\mathrm{36}°=\mathrm{2}{cos}^{\mathrm{2}} {f}−\mathrm{1}. \\ $$$$\therefore{cos}\mathrm{36}°=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}}\Rightarrow\mathrm{2}{cos}\mathrm{36}°=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}. \\ $$$${Hence}\:\frac{{D}}{{s}}=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\blacksquare \\ $$$$ \\ $$

Answered by Rasheed Soomro last updated on 16/Dec/15

Let A,B,C are any three consecutive vertics, then AB^(−) ,BC^(−) are sides of pentagon and AC^(−) is its diagonal Now let mAB^(−) =mBC^(−) =s and mAC^(−) =d We have to prove d:s=(((√5)+1)/2):1 or (d/s)=(((√5)+1)/2) We know that m∠ABC=108° By cosine law d=(√(s^2 +s^2 −2(s)(s) cos 108°)) (d/s)=((√(s^2 +s^2 −2(s)(s) cos 108°))/s) =((s(√(2−2cos 108°)))/s)=(√(2−2cos 108°)) =(√(2−2(((1−(√5))/4))))=(√((8−2+2(√5))/4)) =((√(6+2(√5)))/2) Now we have to change the numerator into a+b(√5) form,where a ,b are rationals So let (√(6+2(√5))) =a+b(√5) 6+2(√5)=(a+b(√5))^2 =a^2 +5b^2 +2ab(√5) a^2 +5b^2 =6 ∧ 2ab=2⇒a=(1/b) a^2 +5b^2 =6⇒((1/b))^2 +5b^2 =6 ⇒1+5b^4 =6b^2 ⇒5b^4 −6b^2 +1=0 ⇒b^2 =((6±(√(36−20)))/(10))=((6±4)/(10))=1,(1/5) ⇒b=±1,±(1/(√5)) [discarding as its irrational] b=±1⇒a=±1 a+b(√5)=1+(√5),1−(√5),−1+(√5),−1−(√5) Last three are extraneous(?) ((√(6+2(√5)))/2)=((1+(√5))/2)

$${Let}\:{A},{B},{C}\:{are}\:{any}\:{three}\:{consecutive}\: \\ $$$${vertics},\:{then}\:\overline {{AB}}\:\:,\overline {{BC}}\:\:{are}\:{sides}\:{of}\: \\ $$$${pentagon}\:{and}\:\overline {{AC}}\:{is}\:{its}\:{diagonal} \\ $$$${Now}\:{let}\:{m}\overline {{AB}}={m}\overline {{BC}}={s} \\ $$$${and}\:\:{m}\overline {{AC}}\:={d} \\ $$$${We}\:{have}\:{to}\:{prove}\:{d}:{s}=\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}}:\mathrm{1} \\ $$$${or}\:\frac{{d}}{{s}}=\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}} \\ $$$${We}\:{know}\:{that}\:{m}\angle{ABC}=\mathrm{108}° \\ $$$${By}\:{cosine}\:{law}\: \\ $$$$\:\:\:\:\:\:\:\:\:{d}=\sqrt{{s}^{\mathrm{2}} +{s}^{\mathrm{2}} −\mathrm{2}\left({s}\right)\left({s}\right)\:\mathrm{cos}\:\mathrm{108}°} \\ $$$$\:\:\:\:\:\:\:\:\frac{{d}}{{s}}=\frac{\sqrt{{s}^{\mathrm{2}} +{s}^{\mathrm{2}} −\mathrm{2}\left({s}\right)\left({s}\right)\:\mathrm{cos}\:\mathrm{108}°}}{{s}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{{s}\sqrt{\mathrm{2}−\mathrm{2cos}\:\mathrm{108}°}}{{s}}=\sqrt{\mathrm{2}−\mathrm{2cos}\:\mathrm{108}°} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\sqrt{\mathrm{2}−\mathrm{2}\left(\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{4}}\right)}=\sqrt{\frac{\mathrm{8}−\mathrm{2}+\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{4}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\frac{\sqrt{\mathrm{6}+\mathrm{2}\sqrt{\mathrm{5}}}}{\mathrm{2}} \\ $$$${Now}\:{we}\:{have}\:{to}\:{change}\:{the}\:{numerator}\:{into} \\ $$$${a}+{b}\sqrt{\mathrm{5}}\:\:{form},{where}\:{a}\:,{b}\:{are}\:{rationals} \\ $$$${So}\:\:{let}\:\:\:\:\sqrt{\mathrm{6}+\mathrm{2}\sqrt{\mathrm{5}}}\:\:={a}+{b}\sqrt{\mathrm{5}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{6}+\mathrm{2}\sqrt{\mathrm{5}}=\left({a}+{b}\sqrt{\mathrm{5}}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={a}^{\mathrm{2}} +\mathrm{5}{b}^{\mathrm{2}} +\mathrm{2}{ab}\sqrt{\mathrm{5}} \\ $$$${a}^{\mathrm{2}} +\mathrm{5}{b}^{\mathrm{2}} =\mathrm{6}\:\:\wedge\:\:\mathrm{2}{ab}=\mathrm{2}\Rightarrow{a}=\frac{\mathrm{1}}{{b}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$${a}^{\mathrm{2}} +\mathrm{5}{b}^{\mathrm{2}} =\mathrm{6}\Rightarrow\left(\frac{\mathrm{1}}{{b}}\right)^{\mathrm{2}} +\mathrm{5}{b}^{\mathrm{2}} =\mathrm{6} \\ $$$$\Rightarrow\mathrm{1}+\mathrm{5}{b}^{\mathrm{4}} =\mathrm{6}{b}^{\mathrm{2}} \Rightarrow\mathrm{5}{b}^{\mathrm{4}} −\mathrm{6}{b}^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{b}^{\mathrm{2}} =\frac{\mathrm{6}\pm\sqrt{\mathrm{36}−\mathrm{20}}}{\mathrm{10}}=\frac{\mathrm{6}\pm\mathrm{4}}{\mathrm{10}}=\mathrm{1},\frac{\mathrm{1}}{\mathrm{5}}\: \\ $$$$\Rightarrow{b}=\pm\mathrm{1},\pm\frac{\mathrm{1}}{\sqrt{\mathrm{5}}}\:\left[{discarding}\:{as}\:{its}\:{irrational}\right] \\ $$$${b}=\pm\mathrm{1}\Rightarrow{a}=\pm\mathrm{1} \\ $$$${a}+{b}\sqrt{\mathrm{5}}=\mathrm{1}+\sqrt{\mathrm{5}},\mathrm{1}−\sqrt{\mathrm{5}},−\mathrm{1}+\sqrt{\mathrm{5}},−\mathrm{1}−\sqrt{\mathrm{5}} \\ $$$${Last}\:{three}\:{are}\:{extraneous}\left(?\right) \\ $$$$\frac{\sqrt{\mathrm{6}+\mathrm{2}\sqrt{\mathrm{5}}}}{\mathrm{2}}=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$

Commented by prakash jain last updated on 16/Dec/15

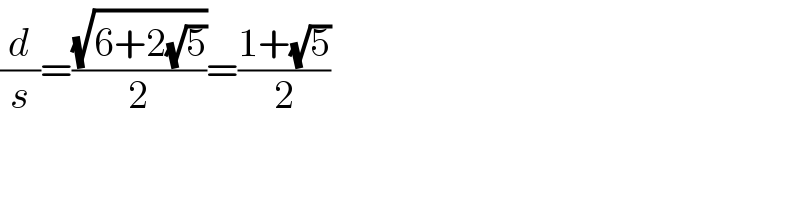
(d/s)=((√(6+2(√5)))/2)=((1+(√5))/2)

$$\frac{{d}}{{s}}=\frac{\sqrt{\mathrm{6}+\mathrm{2}\sqrt{\mathrm{5}}}}{\mathrm{2}}=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\: \\ $$

Commented by Rasheed Soomro last updated on 16/Dec/15

THαnkS!

$$\mathcal{TH}\alpha{n}\Bbbk\mathcal{S}! \\ $$

Answered by Rasheed Soomro last updated on 16/Dec/15

Let A,B,C are three consecutive vertices of a pentagon.Then AB and BC are sides and AC is diagonal of pentagon. m∠ABC=108° △ABC is an issoscel triangle in which let AB=BC=s, AC=d m∠ABC=108° ,m∠CAB=m∠BCA=36° By sine law (d/(sin 108°))=(s/(36°))⇒(d/s)=((sin 108°)/(sin 36°)) =((((√(5+(√5))))/(((√(5−(√5)))))×((((√(5+(√5))))/(((√(5+(√5)))))=((5+(√5))/(√(25−5)))=((5+(√5))/(2(√5))) =(5/(2(√5)))+((√5)/(2(√5)))=((√5)/2)+(1/2)= (d/s)=((1+(√5))/2)

$${Let}\:{A},{B},{C}\:{are}\:{three}\:{consecutive}\:{vertices} \\ $$$${of}\:{a}\:{pentagon}.{Then}\:{AB}\:{and}\:{BC}\:{are}\:{sides} \\ $$$${and}\:{AC}\:{is}\:{diagonal}\:{of}\:{pentagon}.\:{m}\angle{ABC}=\mathrm{108}° \\ $$$$\bigtriangleup{ABC}\:{is}\:{an}\:{issoscel}\:{triangle}\:{in}\:{which}\: \\ $$$$\:{let}\:{AB}={BC}={s},\:{AC}={d} \\ $$$${m}\angle{ABC}=\mathrm{108}°\:,{m}\angle{CAB}={m}\angle{BCA}=\mathrm{36}° \\ $$$${By}\:{sine}\:{law} \\ $$$$\:\:\:\:\frac{{d}}{{sin}\:\mathrm{108}°}=\frac{{s}}{\mathrm{36}°}\Rightarrow\frac{{d}}{{s}}=\frac{{sin}\:\mathrm{108}°}{{sin}\:\mathrm{36}°} \\ $$$$\:\:\:\:\:=\frac{\left(\sqrt{\mathrm{5}+\sqrt{\mathrm{5}}}\right.}{\left(\sqrt{\mathrm{5}−\sqrt{\mathrm{5}}}\right.}×\frac{\left(\sqrt{\mathrm{5}+\sqrt{\mathrm{5}}}\right.}{\left(\sqrt{\mathrm{5}+\sqrt{\mathrm{5}}}\right.}=\frac{\mathrm{5}+\sqrt{\mathrm{5}}}{\sqrt{\mathrm{25}−\mathrm{5}}}=\frac{\mathrm{5}+\sqrt{\mathrm{5}}}{\mathrm{2}\sqrt{\mathrm{5}}} \\ $$$$\:\:\:\:\:=\frac{\mathrm{5}}{\mathrm{2}\sqrt{\mathrm{5}}}+\frac{\sqrt{\mathrm{5}}}{\mathrm{2}\sqrt{\mathrm{5}}}=\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}= \\ $$$$\frac{{d}}{{s}}=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com