Question Number 35895 by ajfour last updated on 25/May/18
Commented by ajfour last updated on 25/May/18
$${Find}\:{the}\:{electric}\:{field}\:{due}\:{to}\:{a} \\ $$$${uniformly}\:{charged}\:{equilateral} \\ $$$${triangular}\:{plate}\:\left({of}\:{charge}\:\right. \\ $$$$\left.{density}\:\sigma\right)\:{on}\:{the}\:{y}\:{axis}\:{at}\:{a}\: \\ $$$${distance}\:{y}\:{from}\:{origin}\:\left({the}\right. \\ $$$$\left.{centroid}\:{of}\:{plate}\right). \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 25/May/18
$${the}\:{elementary}\:{area}\:{as}\:{per}\:{figure}\:{is}\:{dxdz} \\ $$$${for}\:{sign}\:{convenience}\:{let}\:{cosider}\:{the}\:{position} \\ $$$${cooridinate}\:{is}\:\left({x},{z}\right) \\ $$$${electric}\:{field}\:{at}\:{a}\:{distance}\:{y}\:{as}\:{per}\:{figure}\:{is} \\ $$$${dE}=\frac{\mathrm{1}}{\mathrm{4}\Pi\epsilon_{\mathrm{0}} }×\frac{\sigma{dxdy}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} } \\ $$$${now}\:{to}\:{find}\:{limit}\:{of}\:{x}\:{and}\:{z} \\ $$$${centroid}\:{devide}\:{height}\:{of}\:{the}\:{triangle}\:{in}\mathrm{2}:\mathrm{1} \\ $$$${so}\:{deviding}\:\frac{\sqrt{\mathrm{3}}\:{a}}{\mathrm{2}\:}\:{in}\:\mathrm{2}:\mathrm{1}\:{ratio}\:{we}\:{get}\:{the}\:{limit} \\ $$$${of}\:{z}\:\:\:\:{upper}\:{limit}=\frac{\mathrm{2}}{\mathrm{3}}×\frac{\sqrt{\mathrm{3}}\:{a}}{\mathrm{2}},\:{lower}=\frac{\mathrm{1}}{\mathrm{3}}×\frac{\sqrt{\mathrm{3}}\:{a}}{\mathrm{2}} \\ $$$${Z}_{{up}} =\frac{{a}}{\sqrt{\mathrm{3}}}\:\:{Z}_{{low}} =\frac{{a}}{\mathrm{2}\sqrt{\mathrm{3}}}\:{limit}\:{of}\:{z}\:{from}\frac{{a}}{\sqrt{\mathrm{3}}\:}\:{to}\left(−\frac{{a}}{\mathrm{2}\sqrt{\mathrm{3}}}\right. \\ $$$${now}\:{to}\:{find}\:{limit}\:{of}\:{x}\:\:\:\:\:\frac{\mathrm{2}}{\mathrm{3}}=\frac{{x}}{\frac{{a}}{\mathrm{2}}} \\ $$$${x}=\frac{{a}}{\mathrm{3}}\:\:{limit}\:{of}\:{x}\:{is}\:{from}\:−\frac{{a}_{} }{\mathrm{3}}{to}\:+\frac{{a}}{\mathrm{3}} \\ $$$${E}=\frac{\mathrm{1}}{\mathrm{4}\Pi\epsilon_{\mathrm{0}} }×\int_{−\frac{{a}}{\mathrm{3}}} ^{\frac{{a}}{\mathrm{3}}} \int_{−\frac{{a}}{\mathrm{2}\sqrt{\mathrm{3}}}} ^{+\frac{{a}}{\sqrt{\mathrm{3}}}} \frac{\sigma{dxdz}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} }\: \\ $$$${give}\:{me}\:{time}.... \\ $$$$ \\ $$
Commented by ajfour last updated on 25/May/18
$${not}\:{okay},\:{you}\:{are}\:{in}\:{error}.. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 25/May/18
$${true}\: \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 25/May/18
$${why}\:{you}\:{have}\:{taken}\:{dEcos}\theta\:\:{is}\:{there}\:{any}\: \\ $$$$\:\:\:\:\:{symetry}\:{to}\:{cancell}\:{the}\:{dEsin}\theta\:{component}... \\ $$
Commented by ajfour last updated on 25/May/18
$${there}\:{is}\:{such}\:{a}\:{symmetry}. \\ $$
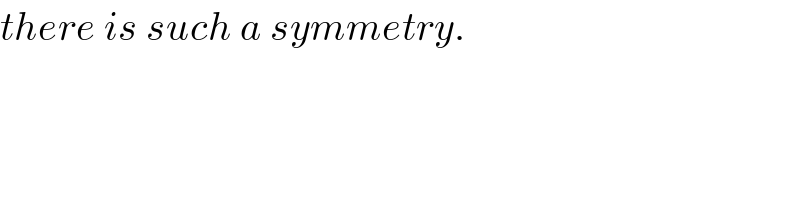
Answered by ajfour last updated on 25/May/18
![dE=(1/(4πε_0 ))(((σdxdz)/(x^2 +y^2 +z^2 ))) E∣_((0,y,0)) =∫∫dEcos θ =(1/(4πε_0 )) ∫_(−(a/2)) ^( (a/2)) [∫_(−(a/(2(√3)))) ^( ((2/3)×(a/2)−x)(√3)) ((σydz)/((x^2 +y^2 +z^2 )^(3/2) ))]dx let z=(√(x^2 +y^2 )) tan φ dz=(√(x^2 +y^2 )) sec^2 φdφ E=((σy)/(4πε_0 ))∫_(−(a/2)) ^( (a/2)) [∫((√(x^2 +y^2 ))/((x^2 +y^2 )^(3/2) sec^3 φ))sec^2 φdφ]dx E=((σy)/(4πε_0 ))∫_(−(a/2)) ^( (a/2)) [∫((cos φdφ)/((x^2 +y^2 )))]dx =((σy)/(4πε_0 ))∫_(−(a/2)) ^( (a/2)) (1/((x^2 +y^2 )))[(z/(√(x^2 +y^2 +z^2 )))]_(−(a/(2(√3)))) ^(((a/3)−x)(√3)) dx =((σy)/(4πε_0 ))∫_(−(a/2)) ^( (a/2)) (1/((x^2 +y^2 )))[((((a/3)−x)(√3))/(√(x^2 +y^2 +3((a/3)−x)^2 )))+((((a/(2(√3)))))/(√(x^2 +y^2 +(a^2 /(12)))))]dx =((σy)/(4πε_0 ))∫_(−(a/2)) ^( (a/2)) [((((a/3)−x)(√3))/((x^2 +y^2 )(√(4x^2 −2ax+(a^2 /3)+y^2 ))))+(a/(2(√3)))×(1/((x^2 +y^2 )(√(x^2 +y^2 +(a^2 /(12))))))]dx =((σy)/(4πε_0 ))∫_(−(a/2)) ^( (a/2)) [((((a/3)−x)(√3))/((x^2 +y^2 )(√((2x−(a/2))^2 +(a^2 /(12))+y^2 ))))+(a/(2(√3)))×(1/((x^2 +y^2 )(√(x^2 +y^2 +(a^2 /(12))))))]dx .....](Q35905.png)
$${dE}=\frac{\mathrm{1}}{\mathrm{4}\pi\epsilon_{\mathrm{0}} }\left(\frac{\sigma{dxdz}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} }\right) \\ $$$${E}\mid_{\left(\mathrm{0},{y},\mathrm{0}\right)} =\int\int{dE}\mathrm{cos}\:\theta \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}\pi\epsilon_{\mathrm{0}} }\:\int_{−\frac{{a}}{\mathrm{2}}} ^{\:\:\frac{{a}}{\mathrm{2}}} \left[\int_{−\frac{{a}}{\mathrm{2}\sqrt{\mathrm{3}}}} ^{\:\:\left(\frac{\mathrm{2}}{\mathrm{3}}×\frac{{a}}{\mathrm{2}}−{x}\right)\sqrt{\mathrm{3}}} \frac{\sigma{ydz}}{\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} }\right]{dx} \\ $$$${let}\:{z}=\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:\mathrm{tan}\:\phi \\ $$$$\:\:\:\:\:\:{dz}=\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\:\mathrm{sec}\:^{\mathrm{2}} \phi{d}\phi \\ $$$${E}=\frac{\sigma{y}}{\mathrm{4}\pi\epsilon_{\mathrm{0}} }\int_{−\frac{{a}}{\mathrm{2}}} ^{\:\:\frac{{a}}{\mathrm{2}}} \left[\int\frac{\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }}{\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} \mathrm{sec}\:^{\mathrm{3}} \phi}\mathrm{sec}\:^{\mathrm{2}} \phi{d}\phi\right]{dx} \\ $$$${E}=\frac{\sigma{y}}{\mathrm{4}\pi\epsilon_{\mathrm{0}} }\int_{−\frac{{a}}{\mathrm{2}}} ^{\:\:\frac{{a}}{\mathrm{2}}} \left[\int\frac{\mathrm{cos}\:\phi{d}\phi}{\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)}\right]{dx} \\ $$$$\:\:=\frac{\sigma{y}}{\mathrm{4}\pi\epsilon_{\mathrm{0}} }\int_{−\frac{{a}}{\mathrm{2}}} ^{\:\:\frac{{a}}{\mathrm{2}}} \frac{\mathrm{1}}{\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)}\left[\frac{{z}}{\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} }}\right]_{−\frac{{a}}{\mathrm{2}\sqrt{\mathrm{3}}}} ^{\left(\frac{{a}}{\mathrm{3}}−{x}\right)\sqrt{\mathrm{3}}} {dx} \\ $$$$\:=\frac{\sigma{y}}{\mathrm{4}\pi\epsilon_{\mathrm{0}} }\int_{−\frac{{a}}{\mathrm{2}}} ^{\:\:\frac{{a}}{\mathrm{2}}} \frac{\mathrm{1}}{\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)}\left[\frac{\left(\frac{{a}}{\mathrm{3}}−{x}\right)\sqrt{\mathrm{3}}}{\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{3}\left(\frac{{a}}{\mathrm{3}}−{x}\right)^{\mathrm{2}} }}+\frac{\left(\frac{{a}}{\mathrm{2}\sqrt{\mathrm{3}}}\right)}{\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\frac{{a}^{\mathrm{2}} }{\mathrm{12}}}}\right]{dx} \\ $$$$\:=\frac{\sigma{y}}{\mathrm{4}\pi\epsilon_{\mathrm{0}} }\int_{−\frac{{a}}{\mathrm{2}}} ^{\:\:\frac{{a}}{\mathrm{2}}} \left[\frac{\left(\frac{{a}}{\mathrm{3}}−{x}\right)\sqrt{\mathrm{3}}}{\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)\sqrt{\mathrm{4}{x}^{\mathrm{2}} −\mathrm{2}{ax}+\frac{{a}^{\mathrm{2}} }{\mathrm{3}}+{y}^{\mathrm{2}} }}+\frac{{a}}{\mathrm{2}\sqrt{\mathrm{3}}}×\frac{\mathrm{1}}{\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\frac{{a}^{\mathrm{2}} }{\mathrm{12}}}}\right]{dx} \\ $$$$\:=\frac{\sigma{y}}{\mathrm{4}\pi\epsilon_{\mathrm{0}} }\int_{−\frac{{a}}{\mathrm{2}}} ^{\:\:\frac{{a}}{\mathrm{2}}} \left[\frac{\left(\frac{{a}}{\mathrm{3}}−{x}\right)\sqrt{\mathrm{3}}}{\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)\sqrt{\left(\mathrm{2}{x}−\frac{{a}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{{a}^{\mathrm{2}} }{\mathrm{12}}+{y}^{\mathrm{2}} }}+\frac{{a}}{\mathrm{2}\sqrt{\mathrm{3}}}×\frac{\mathrm{1}}{\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\frac{{a}^{\mathrm{2}} }{\mathrm{12}}}}\right]{dx} \\ $$$$..... \\ $$