let f(x) = (1/(1+x^3 )) 1) calculate f^((n)) (x) 2) developp f at integr serie.


Question and Answers Forum

All Questions Topic List
Others Questions
Previous in All Question Next in All Question
Previous in Others Next in Others
Question Number 35987 by abdo mathsup 649 cc last updated on 26/May/18

$l e t f (x) = \frac{1}{1 + x^{3}}$ $1) c a l c u l a t e f^{(n)} (x)$ $2) d e v e l o p p f a t i n t e g r s e r i e .$
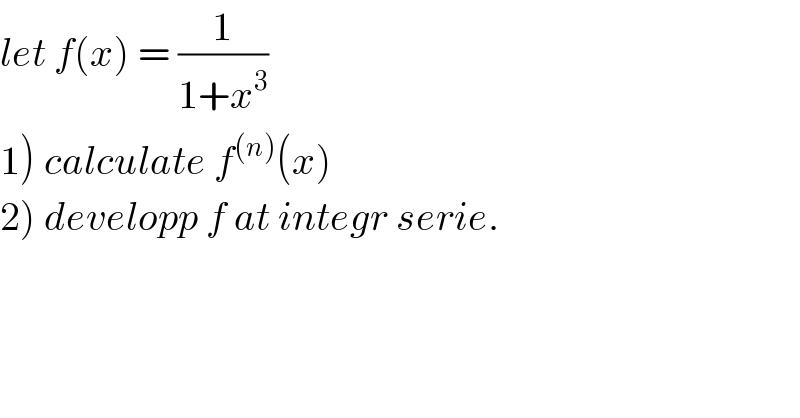
Commented by prof Abdo imad last updated on 27/May/18

$w e h a v e f (x) = \frac{1}{(x + 1) (x^{2} - x + 1)} l e t d e c o m p o s e$ $f i n s i d e C [x] r o o t s o f x^{2} - x + 1$ $Δ = 1 - 4 = - 3 = {(i \sqrt{3})}^{2} \Rightarrow x_{1} = \frac{1 + i \sqrt{3}}{2}$ $x_{2} = \frac{1 - \sqrt{3}}{2} o r j = - \frac{1}{2} + i \frac{\sqrt{3}}{2} \Rightarrow x_{2} = - j a n d$ $x_{1} = - \bar{j} \Rightarrow f (x) = \frac{1}{(x + 1) (x + j) (x + \bar{j})} = \frac{a}{x + 1} + \frac{b}{x + j} + \frac{c}{x + \bar{j}}$ $a = {l i m}_{x \to - 1} (x + 1) f (x) = \frac{1}{3}$ $b = {l i m}_{x \to - j} (x + j) f (x) = \frac{1}{(- j + 1) (- j + \bar{j})}$ $= \frac{1}{(j - 1) (j - \bar{j})} = \frac{1}{\sqrt{3} (- \frac{3}{2} + i \frac{\sqrt{3}}{2})}$ $= \frac{2}{3 (- \sqrt{3} + i)} = \frac{2 (- \sqrt{3} - i)}{3 (3 + 1)} = \frac{- \sqrt{3} - i}{6}$ $c = {l i m}_{x \to - \bar{j}} (x + \bar{j}) f (x) = \frac{1}{(- \bar{j} + 1) (j - \bar{j})}$ $= \frac{1}{\sqrt{3} (\frac{1 + i \sqrt{3}}{2} + 1)} = \frac{1}{\sqrt{3} (\frac{3}{2} + i \frac{\sqrt{3}}{2})}$ $= \frac{2}{3 (\sqrt{3} + i)} = \frac{2 (\sqrt{3} - i)}{3 (4)} = \frac{\sqrt{3} - i}{6} \Rightarrow$ $f (x) = \frac{1}{3 (x + 1)} - \frac{\sqrt{3} + i}{6 (x + j)} + \frac{\sqrt{3} - i}{6 (x + \bar{j})} \Rightarrow$ $f^{(n)} (x) = \frac{1}{3} \frac{{(- 1)}^{n} n!}{{(x + 1)}^{n + 1}} - \frac{\sqrt{3} + i}{6} \frac{{(- 1)}^{n} n!}{{(x + j)}^{n + 1}}$ $+ \frac{\sqrt{3} - i}{6} \frac{{(- 1)}^{n} n!}{{(x + \bar{j})}^{n + 1}}$
Commented by prof Abdo imad last updated on 27/May/18
$f^n (x) = (((−1)^n n!)/(3(x+1)^(n+1) )) + (((−1)^n n!)/6){ (((√3)−i)/((x+j^− )^(n+1) )) −(((√3)+i)/((x+j)^(n+1) ))} f^((n)) (x) = (((−1)^n n!)/(3(x+1)^(n+1) )) +(((−1)^n n!)/6){ ((((√3)−i)/((x+j^− )^(n+1) ))) −conj( (((√3)−i)/((x+j^− )^(n+1) ))) = (((−1)^n n!)/(3(x+1)^(n+1) )) +(((−1)^n n!)/3) Im( (((√3)−i)/((x +j^− )^(n+1) )))$
$f^{n} (x) = \frac{{(- 1)}^{n} n!}{3 {(x + 1)}^{n + 1}} + \frac{{(- 1)}^{n} n!}{6} {\frac{\sqrt{3} - i}{{(x + \bar{j})}^{n + 1}}$ $- \frac{\sqrt{3} + i}{{(x + j)}^{n + 1}}}$ $f^{(n)} (x) = \frac{{(- 1)}^{n} n!}{3 {(x + 1)}^{n + 1}} + \frac{{(- 1)}^{n} n!}{6} {(\frac{\sqrt{3} - i}{{(x + \bar{j})}^{n + 1}})$ $- c o n j (\frac{\sqrt{3} - i}{{(x + \bar{j})}^{n + 1}})$ $= \frac{{(- 1)}^{n} n!}{3 {(x + 1)}^{n + 1}} + \frac{{(- 1)}^{n} n!}{3} I m (\frac{\sqrt{3} - i}{{(x + \bar{j})}^{n + 1}})$
Commented by prof Abdo imad last updated on 27/May/18
$2) we have f(x) = Σ_(n=0) ^∞ ((f^((n)) (0))/(n!)) x^n but f^((n)) (0) = (((−1)^n n!)/3) −(((√3)+i)/6) (((−1)^n n!)/j^(n+1) ) +(((√3)−i)/6) (((−1)^n n!)/j^−^(n+1) ) =(((−1)^n n!)/3) + (((−1)^n n!)/6){ (((√3)−i)/j^−^(n+1) ) −(((√3)+i)/j^(n+1) )} =(((−1)^n n!)/3) +(((−1)^n n!)/6){((((√3)−i)j^(n+1) −((√3)+i)j^−^(n+1) )/1)} = (((−1)^n n!)/3) +(((−1)^n n!)/3) Im{ ((√3)−i)j^(n+1) } but ((√3)−i)j^(n+1) =2 (((√3)/2)−(1/2))(e^(i((2π)/3)) )^(n+1) = 2 e^(−i(π/6)) e^(i(2/3)(n+1)π) = 2 e^(i( ((2(n+1)π)/3)−(π/6))) ⇒$
$2) w e h a v e f (x) = \sum_{n = 0}^{\infty} \frac{f^{(n)} (0)}{n!} x^{n} b u t$ $f^{(n)} (0) = \frac{{(- 1)}^{n} n!}{3} - \frac{\sqrt{3} + i}{6} \frac{{(- 1)}^{n} n!}{j^{n + 1}}$ $+ \frac{\sqrt{3} - i}{6} \frac{{(- 1)}^{n} n!}{\overset{-^{n + 1}}{j}}$ $= \frac{{(- 1)}^{n} n!}{3} + \frac{{(- 1)}^{n} n!}{6} {\frac{\sqrt{3} - i}{\overset{-^{n + 1}}{j}} - \frac{\sqrt{3} + i}{j^{n + 1}}}$ $= \frac{{(- 1)}^{n} n!}{3} + \frac{{(- 1)}^{n} n!}{6} {\frac{(\sqrt{3} - i) j^{n + 1} - (\sqrt{3} + i) \overset{-^{n + 1}}{j}}{1}}$ $= \frac{{(- 1)}^{n} n!}{3} + \frac{{(- 1)}^{n} n!}{3} I m {(\sqrt{3} - i) j^{n + 1}}$ $b u t (\sqrt{3} - i) j^{n + 1} = 2 (\frac{\sqrt{3}}{2} - \frac{1}{2}) {(e^{i \frac{2 π}{3}})}^{n + 1}$ $= 2 e^{- i \frac{π}{6}} e^{i \frac{2}{3} (n + 1) π} = 2 e^{i (\frac{2 (n + 1) π}{3} - \frac{π}{6})} \Rightarrow$
Commented by abdo.msup.com last updated on 27/May/18
$f^((n)) (0) = (((−1)^n n!)/3) +(2/3)(−1)^n n!sin(((2(n+1)π)/3)−(π/6)) ⇒f(x) =Σ_(n=0) ^∞ ((f^((n)) (0))/(n!))x^n =Σ_(n=0) ^∞ (((−1)^n )/3){ 1 +2sin(((2(n+1)π)/3) −(π/6))}x^n another method we have f(x) =(1/(1+x^3 )) so for ∣x∣<1 f(x) =Σ_(n=0) ^∞ (−1)^n x^(3n) .$
$f^{(n)} (0) = \frac{{(- 1)}^{n} n!}{3} + \frac{2}{3} {(- 1)}^{n} n! s i n (\frac{2 (n + 1) π}{3} - \frac{π}{6})$ $\Rightarrow f (x) = \sum_{n = 0}^{\infty} \frac{f^{(n)} (0)}{n!} x^{n}$ $= \sum_{n = 0}^{\infty} \frac{{(- 1)}^{n}}{3} {1 + 2 s i n (\frac{2 (n + 1) π}{3} - \frac{π}{6})} x^{n}$ $a n o t h e r m e t h o d$ $w e h a v e f (x) = \frac{1}{1 + x^{3}} s o f o r ∣ x ∣< 1$ $f (x) = \sum_{n = 0}^{\infty} {(- 1)}^{n} x^{3 n} .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum