
Question and Answers Forum
Question Number 35990 by abdo mathsup 649 cc last updated on 26/May/18
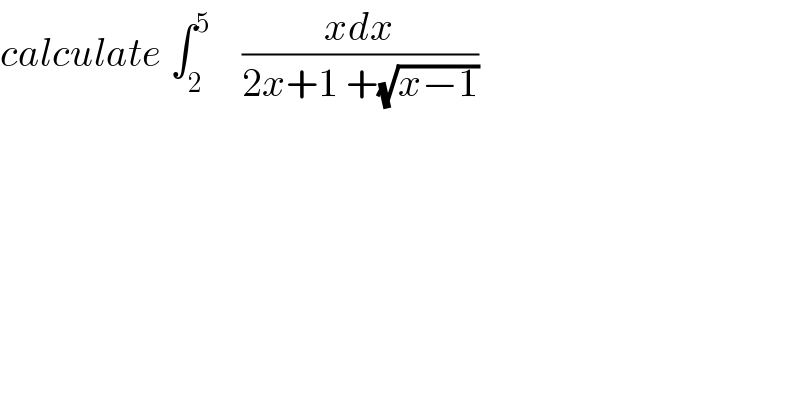
Commented by abdo mathsup 649 cc last updated on 27/May/18
![let put I = ∫_2 ^5 ((xdx)/(2x+1+(√(x−1)))) changement (√(x−1))=t give x =t^2 +1 and I = ∫_1 ^2 ((t^2 +1)/(2t^2 +2+1 +t)) (2t)dt = ∫_1 ^2 ((2t^3 +2t)/(2t^2 +t+3))dt = ∫_1 ^2 ((t( 2t^2 +t+3) −t^2 −3t +2t)/(2t^2 +t +3))dt = ∫_1 ^2 t dt −∫_1 ^2 ((t^2 +t)/(2t^2 +t +3))dt but ∫_1 ^2 t dt =[(t^2 /2)]_1 ^2 = 2−(1/2) =(3/2) ∫_1 ^2 ((t^2 +t)/(2t^2 +t +3))dt =(1/2) ∫_1 ^2 ((2t^2 +t+t +3−3)/(2t^2 +t +3))dt =(1/2) ∫_1 ^2 dt +(1/2) ∫_1 ^2 ((t−3)/(2t^2 +t+3))dt =(1/2) +(1/8)∫_1 ^2 ((4t −12)/(2t^2 +t +3))dt =(1/2) +(1/8) J J = ∫_1 ^2 ((4t+1−13)/(2t^2 +t+3))dt =[ln(2t^2 +t+3)]_1 ^2 −13 ∫_1 ^2 (dt/(2t^2 +t+3)) = ln(13)−ln(6) −((13)/2) ∫_1 ^2 (dt/(t^2 +(t/2) +(3/2))) but t^2 +(t/2) +(3/2) =t^2 +2(1/4)t +(1/(16)) +(3/2) −(1/(16)) =(t +(1/4))^2 + ((23)/(16)) chang. t+(1/4) =((√(23))/4) x give ∫_1 ^2 (dt/(t^2 +(t/2)+(3/2))) = ∫_((1/(√(23)))(5)) ^(9/(√(23))) (1/(((23)/(16))(1+x^2 ))) ((√(23))/4) dx = ((16)/(23)) ((√(23))/4) ∫_(5/(√(23))) ^(9/(√(23))) (dx/(1+x^2 )) =(4/(√(23))){ arctan((9/(√(2)))))−arctan((5/(√(23))))} I =(3/2) −(1/2) −(1/8)J =1 −(1/8){ln(13)−ln(6)−((13)/2)(4/(√(23))){arctan((9/(√(23))))−arctan((5/(√(23))))}o](Q36044.png)
Commented by abdo mathsup 649 cc last updated on 27/May/18
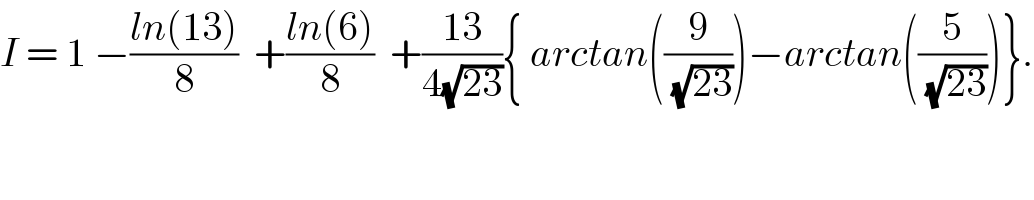
| ||
Question and Answers Forum | ||
Question Number 35990 by abdo mathsup 649 cc last updated on 26/May/18 | ||
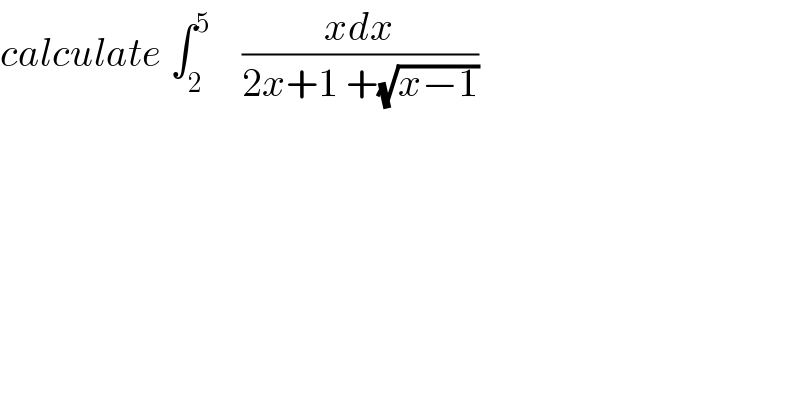 | ||
Commented by abdo mathsup 649 cc last updated on 27/May/18 | ||
![let put I = ∫_2 ^5 ((xdx)/(2x+1+(√(x−1)))) changement (√(x−1))=t give x =t^2 +1 and I = ∫_1 ^2 ((t^2 +1)/(2t^2 +2+1 +t)) (2t)dt = ∫_1 ^2 ((2t^3 +2t)/(2t^2 +t+3))dt = ∫_1 ^2 ((t( 2t^2 +t+3) −t^2 −3t +2t)/(2t^2 +t +3))dt = ∫_1 ^2 t dt −∫_1 ^2 ((t^2 +t)/(2t^2 +t +3))dt but ∫_1 ^2 t dt =[(t^2 /2)]_1 ^2 = 2−(1/2) =(3/2) ∫_1 ^2 ((t^2 +t)/(2t^2 +t +3))dt =(1/2) ∫_1 ^2 ((2t^2 +t+t +3−3)/(2t^2 +t +3))dt =(1/2) ∫_1 ^2 dt +(1/2) ∫_1 ^2 ((t−3)/(2t^2 +t+3))dt =(1/2) +(1/8)∫_1 ^2 ((4t −12)/(2t^2 +t +3))dt =(1/2) +(1/8) J J = ∫_1 ^2 ((4t+1−13)/(2t^2 +t+3))dt =[ln(2t^2 +t+3)]_1 ^2 −13 ∫_1 ^2 (dt/(2t^2 +t+3)) = ln(13)−ln(6) −((13)/2) ∫_1 ^2 (dt/(t^2 +(t/2) +(3/2))) but t^2 +(t/2) +(3/2) =t^2 +2(1/4)t +(1/(16)) +(3/2) −(1/(16)) =(t +(1/4))^2 + ((23)/(16)) chang. t+(1/4) =((√(23))/4) x give ∫_1 ^2 (dt/(t^2 +(t/2)+(3/2))) = ∫_((1/(√(23)))(5)) ^(9/(√(23))) (1/(((23)/(16))(1+x^2 ))) ((√(23))/4) dx = ((16)/(23)) ((√(23))/4) ∫_(5/(√(23))) ^(9/(√(23))) (dx/(1+x^2 )) =(4/(√(23))){ arctan((9/(√(2)))))−arctan((5/(√(23))))} I =(3/2) −(1/2) −(1/8)J =1 −(1/8){ln(13)−ln(6)−((13)/2)(4/(√(23))){arctan((9/(√(23))))−arctan((5/(√(23))))}o](Q36044.png) | ||
Commented by abdo mathsup 649 cc last updated on 27/May/18 | ||
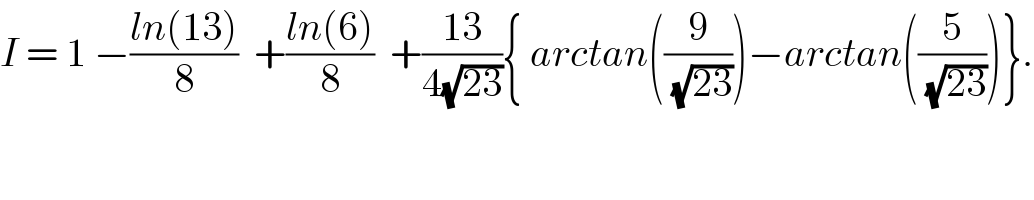 | ||