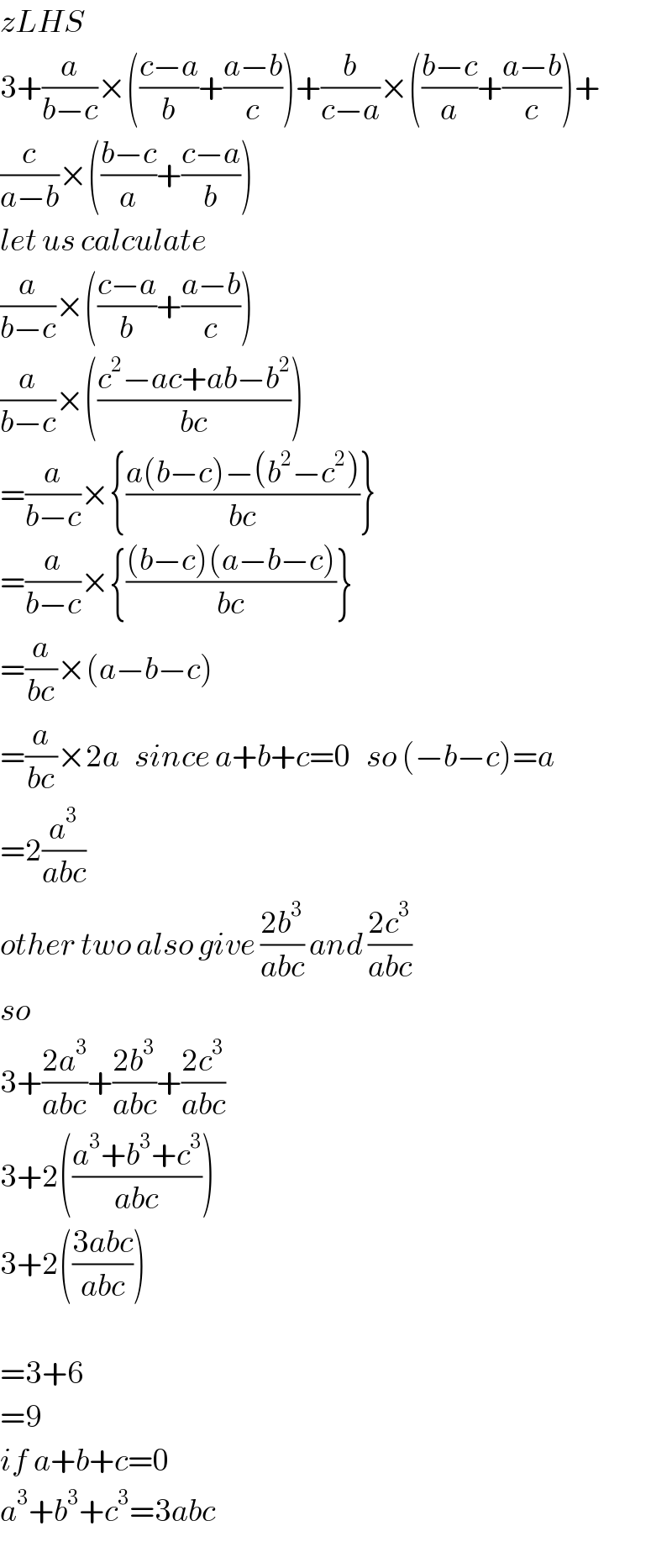Question Number 36019 by math1967 last updated on 27/May/18
$${If}\:{a}+{b}+{c}=\mathrm{0}\:{show}\:{that} \\ $$$$\left(\frac{{a}}{{b}−{c}}+\frac{{b}}{{c}−{a}}+\frac{{c}}{{a}−{b}}\right)\left(\frac{{b}−{c}}{{a}}+\frac{{c}−{a}}{{b}}\:+\frac{{a}−{b}}{{c}}\right)=\mathrm{9} \\ $$
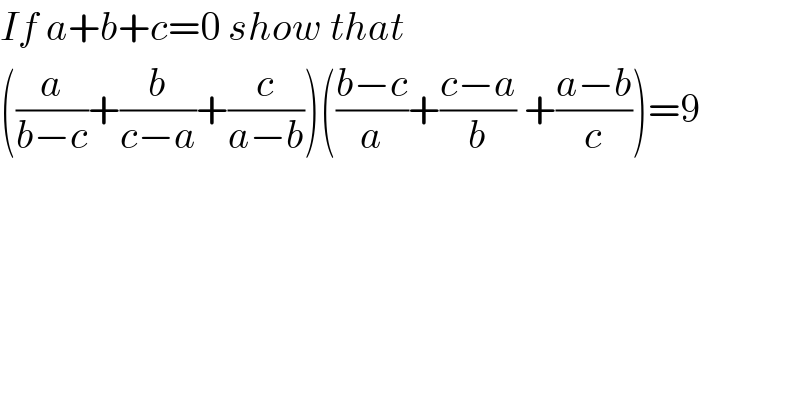
Answered by ajfour last updated on 27/May/18
![let b=pa , c=qa ⇒ a(1+p+q)=0 ...(i) (shall be using this in many steps that follow..) l.h.s. = ((1/(p−q))+(p/(q−1))+(q/(1−p)))(((p−q)/1)+((q−1)/p)+((1−p)/q)) =1+(((q−1))/(p(p−q)))+(((1−p))/(q(p−q)))+ ((p(p−q))/(q−1))+1+((p(1−p))/(q(q−1)))+ ((q(p−q))/((1−p)))+((q(q−1))/(p(1−p)))+1 =3+((q^2 −q+p−p^2 )/(pq(p−q)))+((pq(p−q)+p(1−p))/(q(q−1)))+ ((pq(p−q)+q(q−1))/(p(1−p))) =3+((1−p−q)/(pq))+((p[qp−q^2 +1−p])/(q(q−1)))+ ((q[p^2 −pq+q−1])/(p(1−p))) =3+(2/(pq))+((p(p−q−1))/q)+((q(q−p−1))/p) =3+((2+p^2 (p−q−1)+q^2 (q−p−1))/(pq)) =3+((2+p^3 +q^3 −pq(p+q)−(p^2 +q^2 ))/(pq)) =3+((2−(p^2 +q^2 −pq)+pq−1+2pq)/(pq)) =3+((2−1+2pq+pq+pq−1+2pq)/(pq)) = 3+6 = 9 .](Q36020.png)
$${let}\:{b}={pa}\:\:,\:\:{c}={qa} \\ $$$$\Rightarrow\:{a}\left(\mathrm{1}+{p}+{q}\right)=\mathrm{0}\:\:\:\:\:\:\:\:\:\:...\left({i}\right) \\ $$$$\:\:\:\left({shall}\:{be}\:{using}\:{this}\:{in}\:{many}\right. \\ $$$$\left.\:\:\:\:\:\:{steps}\:{that}\:{follow}..\right) \\ $$$${l}.{h}.{s}.\:=\:\left(\frac{\mathrm{1}}{{p}−{q}}+\frac{{p}}{{q}−\mathrm{1}}+\frac{{q}}{\mathrm{1}−{p}}\right)\left(\frac{{p}−{q}}{\mathrm{1}}+\frac{{q}−\mathrm{1}}{{p}}+\frac{\mathrm{1}−{p}}{{q}}\right) \\ $$$$\:\:\:=\mathrm{1}+\frac{\left({q}−\mathrm{1}\right)}{{p}\left({p}−{q}\right)}+\frac{\left(\mathrm{1}−{p}\right)}{{q}\left({p}−{q}\right)}+ \\ $$$$\:\:\:\:\:\:\frac{{p}\left({p}−{q}\right)}{{q}−\mathrm{1}}+\mathrm{1}+\frac{{p}\left(\mathrm{1}−{p}\right)}{{q}\left({q}−\mathrm{1}\right)}+ \\ $$$$\:\:\:\:\:\:\:\:\:\:\frac{{q}\left({p}−{q}\right)}{\left(\mathrm{1}−{p}\right)}+\frac{{q}\left({q}−\mathrm{1}\right)}{{p}\left(\mathrm{1}−{p}\right)}+\mathrm{1} \\ $$$$\:\:\:=\mathrm{3}+\frac{{q}^{\mathrm{2}} −{q}+{p}−{p}^{\mathrm{2}} }{{pq}\left({p}−{q}\right)}+\frac{{pq}\left({p}−{q}\right)+{p}\left(\mathrm{1}−{p}\right)}{{q}\left({q}−\mathrm{1}\right)}+ \\ $$$$\:\:\:\:\:\:\:\:\frac{{pq}\left({p}−{q}\right)+{q}\left({q}−\mathrm{1}\right)}{{p}\left(\mathrm{1}−{p}\right)} \\ $$$$\:\:\:=\mathrm{3}+\frac{\mathrm{1}−{p}−{q}}{{pq}}+\frac{{p}\left[{qp}−{q}^{\mathrm{2}} +\mathrm{1}−{p}\right]}{{q}\left({q}−\mathrm{1}\right)}+ \\ $$$$\:\:\:\:\:\:\:\:\:\:\frac{{q}\left[{p}^{\mathrm{2}} −{pq}+{q}−\mathrm{1}\right]}{{p}\left(\mathrm{1}−{p}\right)} \\ $$$$\:\:\:=\mathrm{3}+\frac{\mathrm{2}}{{pq}}+\frac{{p}\left({p}−{q}−\mathrm{1}\right)}{{q}}+\frac{{q}\left({q}−{p}−\mathrm{1}\right)}{{p}} \\ $$$$\:\:\:=\mathrm{3}+\frac{\mathrm{2}+{p}^{\mathrm{2}} \left({p}−{q}−\mathrm{1}\right)+{q}^{\mathrm{2}} \left({q}−{p}−\mathrm{1}\right)}{{pq}} \\ $$$$\:\:\:=\mathrm{3}+\frac{\mathrm{2}+{p}^{\mathrm{3}} +{q}^{\mathrm{3}} −{pq}\left({p}+{q}\right)−\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)}{{pq}} \\ $$$$\:\:=\mathrm{3}+\frac{\mathrm{2}−\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} −{pq}\right)+{pq}−\mathrm{1}+\mathrm{2}{pq}}{{pq}} \\ $$$$\:\:=\mathrm{3}+\frac{\mathrm{2}−\mathrm{1}+\mathrm{2}{pq}+{pq}+{pq}−\mathrm{1}+\mathrm{2}{pq}}{{pq}} \\ $$$$\:\:=\:\mathrm{3}+\mathrm{6}\:=\:\mathrm{9}\:. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 27/May/18
$${praisworthy}... \\ $$
Answered by ajfour last updated on 27/May/18
![l.h.s. = 3+Σ((a/(b−c)))[(((c−a)/b))+(((a−b)/c))] =3+Σ((a/(b−c)))(((c^2 −ac+ab−b^2 )/(bc))) =3+Σ((a^2 /(abc)))(a−b−c) =3+Σ((a^2 /(abc)))(2a) ∵ (−b−c=a) =3+2Σ(a^3 /(abc)) and as Σa^3 =3abc if Σa=0, so l.h.s. =3+2(((3abc)/(abc)))= 9 .](Q36028.png)
$${l}.{h}.{s}.\:=\:\mathrm{3}+\Sigma\left(\frac{{a}}{{b}−{c}}\right)\left[\left(\frac{{c}−{a}}{{b}}\right)+\left(\frac{{a}−{b}}{{c}}\right)\right] \\ $$$$\:\:\:\:\:=\mathrm{3}+\Sigma\left(\frac{{a}}{{b}−{c}}\right)\left(\frac{{c}^{\mathrm{2}} −{ac}+{ab}−{b}^{\mathrm{2}} }{{bc}}\right) \\ $$$$\:\:\:\:\:=\mathrm{3}+\Sigma\left(\frac{{a}^{\mathrm{2}} }{{abc}}\right)\left({a}−{b}−{c}\right) \\ $$$$\:\:\:\:\:=\mathrm{3}+\Sigma\left(\frac{{a}^{\mathrm{2}} }{{abc}}\right)\left(\mathrm{2}{a}\right)\:\:\:\:\:\because\:\left(−{b}−{c}={a}\right) \\ $$$$\:\:\:\:\:=\mathrm{3}+\mathrm{2}\Sigma\frac{{a}^{\mathrm{3}} }{{abc}} \\ $$$${and}\:{as}\:\:\Sigma{a}^{\mathrm{3}} =\mathrm{3}{abc}\:\:{if}\:\:\Sigma{a}=\mathrm{0},\:{so} \\ $$$$\:\:{l}.{h}.{s}.\:\:=\mathrm{3}+\mathrm{2}\left(\frac{\mathrm{3}{abc}}{{abc}}\right)=\:\mathrm{9}\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 28/May/18
$${zLHS} \\ $$$$\mathrm{3}+\frac{{a}}{{b}−{c}}×\left(\frac{{c}−{a}}{{b}}+\frac{{a}−{b}}{{c}}\right)+\frac{{b}}{{c}−{a}}×\left(\frac{{b}−{c}}{{a}}+\frac{{a}−{b}}{{c}}\right)+ \\ $$$$\frac{{c}}{{a}−{b}}×\left(\frac{{b}−{c}}{{a}}+\frac{{c}−{a}}{{b}}\right) \\ $$$${let}\:{us}\:{calculate}\: \\ $$$$\frac{{a}}{{b}−{c}}×\left(\frac{{c}−{a}}{{b}}+\frac{{a}−{b}}{{c}}\right) \\ $$$$\frac{{a}}{{b}−{c}}×\left(\frac{{c}^{\mathrm{2}} −{ac}+{ab}−{b}^{\mathrm{2}} }{{bc}}\right) \\ $$$$=\frac{{a}}{{b}−{c}}×\left\{\frac{{a}\left({b}−{c}\right)−\left({b}^{\mathrm{2}} −{c}^{\mathrm{2}} \right)}{{bc}}\right\} \\ $$$$=\frac{{a}}{{b}−{c}}×\left\{\frac{\left({b}−{c}\right)\left({a}−{b}−{c}\right)}{{bc}}\right\} \\ $$$$=\frac{{a}}{{bc}}×\left({a}−{b}−{c}\right) \\ $$$$=\frac{{a}}{{bc}}×\mathrm{2}{a}\:\:\:{since}\:{a}+{b}+{c}=\mathrm{0}\:\:\:{so}\:\left(−{b}−{c}\right)={a} \\ $$$$=\mathrm{2}\frac{{a}^{\mathrm{3}} }{{abc}} \\ $$$${other}\:{two}\:{also}\:{give}\:\frac{\mathrm{2}{b}^{\mathrm{3}} }{{abc}}\:{and}\:\frac{\mathrm{2}{c}^{\mathrm{3}} }{{abc}} \\ $$$${so} \\ $$$$\mathrm{3}+\frac{\mathrm{2}{a}^{\mathrm{3}} }{{abc}}+\frac{\mathrm{2}{b}^{\mathrm{3}} }{{abc}}+\frac{\mathrm{2}{c}^{\mathrm{3}} }{{abc}} \\ $$$$\mathrm{3}+\mathrm{2}\left(\frac{{a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} }{{abc}}\right) \\ $$$$\mathrm{3}+\mathrm{2}\left(\frac{\mathrm{3}{abc}}{{abc}}\right)\: \\ $$$$ \\ $$$$=\mathrm{3}+\mathrm{6} \\ $$$$=\mathrm{9} \\ $$$${if}\:{a}+{b}+{c}=\mathrm{0} \\ $$$${a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} =\mathrm{3}{abc} \\ $$