
Question and Answers Forum
Question Number 36180 by prof Abdo imad last updated on 30/May/18
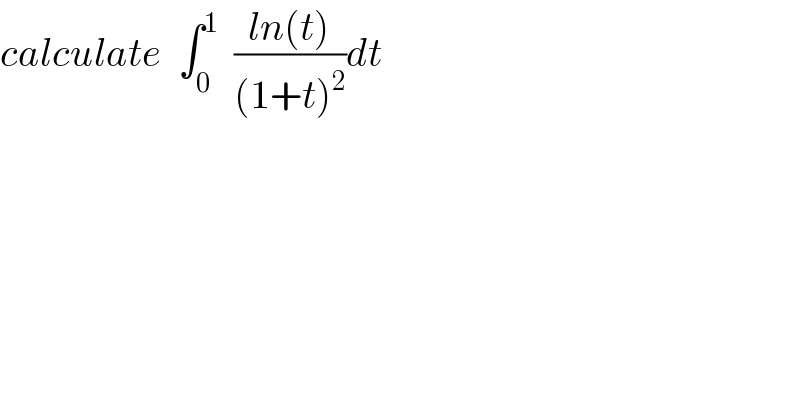
Commented by prof Abdo imad last updated on 30/May/18
![let put I = ∫_0 ^1 ((ln(t))/((1+t)^2 ))dt let integrate by parts I =[(1−(1/(1+t)))ln(t)]_0 ^1 −∫_0 ^1 (1−(1/(1+t)))(dt/t) =0 − ∫_0 ^1 (dt/(1+t)) =−[ln∣1+t∣]_0 ^1 =−ln(2) let prove that lim_(t→0) (1−(1/(1+t)))ln(t)=0 lim_(t→0) (1−(1/(1+t)))ln(t) =lim_(t→0) ((tln(t))/(1+t)) =0 because lim_(t→0) tln(t) =0 so ★ ∫_0 ^1 ((ln(t))/((1+t)^2 ))dt =−ln(2)★](Q36261.png)
Answered by sma3l2996 last updated on 30/May/18
![I=∫_0 ^1 ((lnt)/((1+t)^2 ))dt by parts u=lnt⇒u′=(1/t) v′=(1/((1+t)^2 ))⇒v=−(1/(1+t)) I=[−((lnt)/(1+t))]_0 ^1 +∫_0 ^1 (dt/(t(1+t))) =lim_(t→0^+ ) ((lnt)/(1+t))+∫_0 ^1 ((1/t)−(1/(1+t)))dt =lim_(t→0^+ ) ((lnt)/(1+t))+[ln((t/(1+t)))]_0 ^1 =lim_(t→0^+ ) (((lnt)/(1+t))−ln(t))−ln2 =−lim_(x→0^+ ) ((tln(t))/(1+t))−ln2=−ln2 (because lim_(x→0^+ ) xlnx=0)](Q36199.png)
| ||
Question and Answers Forum | ||
Question Number 36180 by prof Abdo imad last updated on 30/May/18 | ||
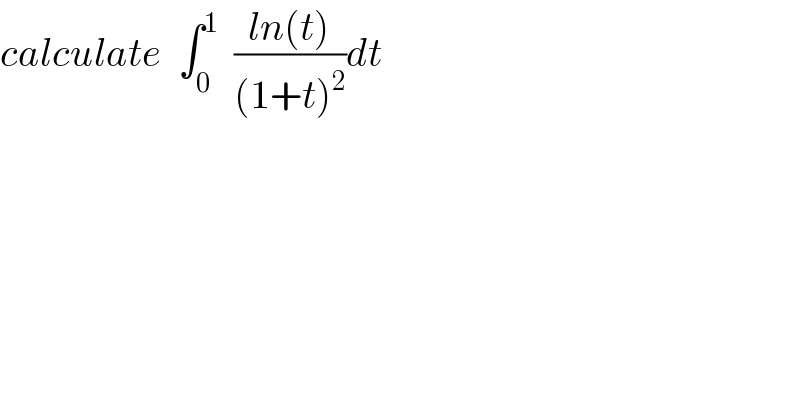 | ||
Commented by prof Abdo imad last updated on 30/May/18 | ||
![let put I = ∫_0 ^1 ((ln(t))/((1+t)^2 ))dt let integrate by parts I =[(1−(1/(1+t)))ln(t)]_0 ^1 −∫_0 ^1 (1−(1/(1+t)))(dt/t) =0 − ∫_0 ^1 (dt/(1+t)) =−[ln∣1+t∣]_0 ^1 =−ln(2) let prove that lim_(t→0) (1−(1/(1+t)))ln(t)=0 lim_(t→0) (1−(1/(1+t)))ln(t) =lim_(t→0) ((tln(t))/(1+t)) =0 because lim_(t→0) tln(t) =0 so ★ ∫_0 ^1 ((ln(t))/((1+t)^2 ))dt =−ln(2)★](Q36261.png) | ||
Answered by sma3l2996 last updated on 30/May/18 | ||
![I=∫_0 ^1 ((lnt)/((1+t)^2 ))dt by parts u=lnt⇒u′=(1/t) v′=(1/((1+t)^2 ))⇒v=−(1/(1+t)) I=[−((lnt)/(1+t))]_0 ^1 +∫_0 ^1 (dt/(t(1+t))) =lim_(t→0^+ ) ((lnt)/(1+t))+∫_0 ^1 ((1/t)−(1/(1+t)))dt =lim_(t→0^+ ) ((lnt)/(1+t))+[ln((t/(1+t)))]_0 ^1 =lim_(t→0^+ ) (((lnt)/(1+t))−ln(t))−ln2 =−lim_(x→0^+ ) ((tln(t))/(1+t))−ln2=−ln2 (because lim_(x→0^+ ) xlnx=0)](Q36199.png) | ||
| ||