
Question and Answers Forum
Question Number 36181 by prof Abdo imad last updated on 30/May/18
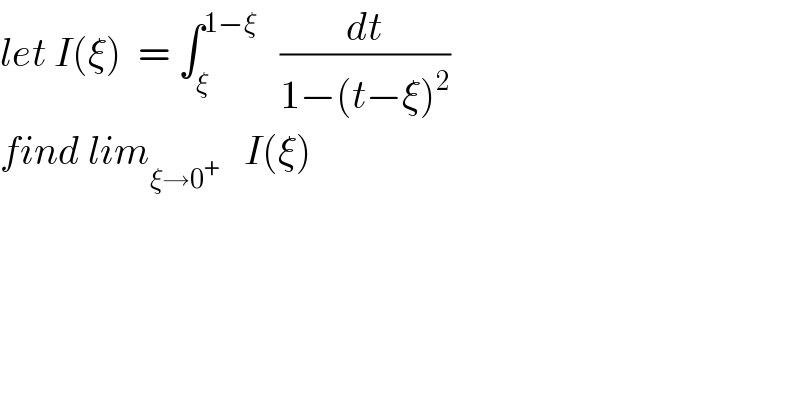
Commented by maxmathsup by imad last updated on 20/Aug/18
![changement t−ξ =sinα give α =arcsin(t−ξ) ⇒ I(ξ) = ∫_0 ^(arcsin(1−2ξ)) ((cosα dα)/(1−sin^2 α)) =∫_0 ^(arcsin(1−2ξ)) (dα/(cosα)) =_(tan((α/2))=u) ∫_0 ^(tan(((arcsin(1−2ξ))/2))) (1/((1−u^2 )/(1+u^2 ))) ((2du)/(1+u^2 )) = ∫_0 ^(tan(((arcsin(1−2ξ))/2))) ((2du)/(1−u^2 )) = ∫_0 ^(tan(((arcsin(1−2ξ))/2))) ((1/(1+u)) +(1/(1−u)))du =[ln∣((1+u)/(1−u))∣]_0 ^(tan(((arcsin(1−2ξ))/2))) =ln∣ ((1+tan(((arcsin(1−2ξ))/2)))/(1−tan(((arcsin(1−2ξ))/2))))∣ ⇒lim_(ξ→0^+ ) I(ξ) =ln∣ ((1 +tan((π/4)))/(1−tan((π/4))))∣ =+∞ .](Q42238.png)
| ||
Question and Answers Forum | ||
Question Number 36181 by prof Abdo imad last updated on 30/May/18 | ||
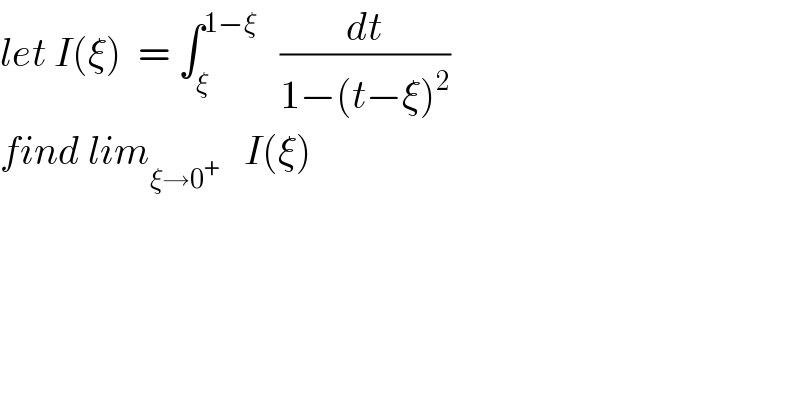 | ||
Commented by maxmathsup by imad last updated on 20/Aug/18 | ||
![changement t−ξ =sinα give α =arcsin(t−ξ) ⇒ I(ξ) = ∫_0 ^(arcsin(1−2ξ)) ((cosα dα)/(1−sin^2 α)) =∫_0 ^(arcsin(1−2ξ)) (dα/(cosα)) =_(tan((α/2))=u) ∫_0 ^(tan(((arcsin(1−2ξ))/2))) (1/((1−u^2 )/(1+u^2 ))) ((2du)/(1+u^2 )) = ∫_0 ^(tan(((arcsin(1−2ξ))/2))) ((2du)/(1−u^2 )) = ∫_0 ^(tan(((arcsin(1−2ξ))/2))) ((1/(1+u)) +(1/(1−u)))du =[ln∣((1+u)/(1−u))∣]_0 ^(tan(((arcsin(1−2ξ))/2))) =ln∣ ((1+tan(((arcsin(1−2ξ))/2)))/(1−tan(((arcsin(1−2ξ))/2))))∣ ⇒lim_(ξ→0^+ ) I(ξ) =ln∣ ((1 +tan((π/4)))/(1−tan((π/4))))∣ =+∞ .](Q42238.png) | ||