
Question Number 36182 by prof Abdo imad last updated on 30/May/18
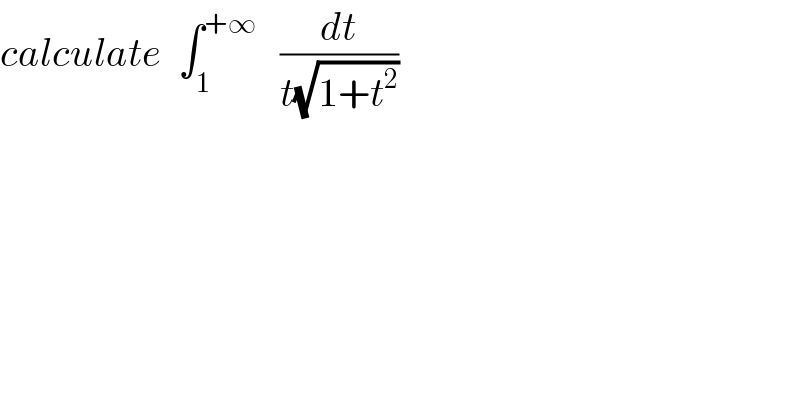
$${calculate}\:\:\int_{\mathrm{1}} ^{+\infty} \:\:\:\frac{{dt}}{{t}\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }} \\ $$
Commented by maxmathsup by imad last updated on 15/Aug/18
![let I = ∫_1 ^(+∞) (dt/(t(√(1+t^2 )))) dt changement t =sh(x) give I = ∫_(argsh(1)) ^(+∞) (1/(sh(x)ch(x))) ch(x)dx = ∫_(ln(1+(√2))) ^(+∞) (dx/(sh(x))) = ∫_(ln(1+(√2))) ^(+∞) ((2dx)/(e^x −e^(−x) )) = ∫_(ln(1+(√2))) ^(+∞) ((2 e^x )/(e^(2x) −1))dx =_(e^x =u) ∫_(1+(√2)) ^(+∞) ((2u)/(u^2 −1)) (du/u) = ∫_(1+(√2)) ^(+∞) ((2du)/(u^2 −1)) = ∫_(1+(√2)) ^(+∞) ( (1/(u−1)) −(1/(u+1)))du =[ln∣((u−1)/(u+1))∣]_(1+(√2)) ^(+∞) =−ln∣ ((√2)/(2+(√2))) ∣ =−ln(((√2)/(√(2(1+(√2))))))=ln(1+(√2)) ⇒ I =ln(1+(√2)) .](Q41951.png)
$${let}\:{I}\:\:=\:\int_{\mathrm{1}} ^{+\infty} \:\:\:\frac{{dt}}{{t}\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}\:{dt}\:\:{changement}\:{t}\:={sh}\left({x}\right)\:{give} \\ $$$${I}\:=\:\int_{{argsh}\left(\mathrm{1}\right)} ^{+\infty} \:\:\:\frac{\mathrm{1}}{{sh}\left({x}\right){ch}\left({x}\right)}\:{ch}\left({x}\right){dx}\:=\:\int_{{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} ^{+\infty} \:\:\:\:\frac{{dx}}{{sh}\left({x}\right)} \\ $$$$=\:\int_{{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} ^{+\infty} \:\:\:\frac{\mathrm{2}{dx}}{{e}^{{x}} \:−{e}^{−{x}} }\:\:=\:\int_{{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} ^{+\infty} \:\:\frac{\mathrm{2}\:{e}^{{x}} }{{e}^{\mathrm{2}{x}} −\mathrm{1}}{dx}\:=_{{e}^{{x}} \:={u}} \:\:\int_{\mathrm{1}+\sqrt{\mathrm{2}}} ^{+\infty} \:\:\:\frac{\mathrm{2}{u}}{{u}^{\mathrm{2}} −\mathrm{1}}\:\frac{{du}}{{u}} \\ $$$$=\:\int_{\mathrm{1}+\sqrt{\mathrm{2}}} ^{+\infty} \:\:\:\frac{\mathrm{2}{du}}{{u}^{\mathrm{2}} −\mathrm{1}}\:=\:\int_{\mathrm{1}+\sqrt{\mathrm{2}}} ^{+\infty} \:\:\left(\:\:\frac{\mathrm{1}}{{u}−\mathrm{1}}\:−\frac{\mathrm{1}}{{u}+\mathrm{1}}\right){du} \\ $$$$=\left[{ln}\mid\frac{{u}−\mathrm{1}}{{u}+\mathrm{1}}\mid\right]_{\mathrm{1}+\sqrt{\mathrm{2}}} ^{+\infty} \:\:=−{ln}\mid\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}+\sqrt{\mathrm{2}}}\:\mid\:=−{ln}\left(\frac{\sqrt{\mathrm{2}}}{\sqrt{\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)}}\right)={ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\:\Rightarrow \\ $$$${I}\:={ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\:. \\ $$$$ \\ $$
Answered by sma3l2996 last updated on 31/May/18
![L=∫_1 ^(+∞) (dt/(t(√(1+t^2 )))) let t=sinhx⇒dt=coshxdx L=∫_(ln((√2)+1)) ^(+∞) ((coshx)/(sinhx(√(1+sinh^2 x))))dx =∫_(ln((√2)+1)) ^(+∞) (dx/(sinh(x)))=2∫_(ln((√2)+1)) ^(+∞) (e^x /(e^(2x) −1))dx u=e^x ⇒du=e^x dx L=2∫_((√2)+1) ^(+∞) (du/(u^2 −1))=2∫_((√2)+1) ^(+∞) (du/((u+1)(u−1))) =∫_((√2)+1) ^(+∞) ((1/(u−1))−(1/(u+1)))du =[ln∣((u−1)/(u+1))∣]_((√2)+1) ^(+∞) =ln∣(((√2)+2)/(√2))∣= L=ln((√2)+1)](Q36273.png)
$${L}=\int_{\mathrm{1}} ^{+\infty} \frac{{dt}}{{t}\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }} \\ $$$${let}\:\:{t}={sinhx}\Rightarrow{dt}={coshxdx} \\ $$$${L}=\int_{{ln}\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)} ^{+\infty} \frac{{coshx}}{{sinhx}\sqrt{\mathrm{1}+{sinh}^{\mathrm{2}} {x}}}{dx} \\ $$$$=\int_{{ln}\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)} ^{+\infty} \frac{{dx}}{{sinh}\left({x}\right)}=\mathrm{2}\int_{{ln}\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)} ^{+\infty} \frac{{e}^{{x}} }{{e}^{\mathrm{2}{x}} −\mathrm{1}}{dx} \\ $$$${u}={e}^{{x}} \Rightarrow{du}={e}^{{x}} {dx} \\ $$$${L}=\mathrm{2}\int_{\sqrt{\mathrm{2}}+\mathrm{1}} ^{+\infty} \frac{{du}}{{u}^{\mathrm{2}} −\mathrm{1}}=\mathrm{2}\int_{\sqrt{\mathrm{2}}+\mathrm{1}} ^{+\infty} \frac{{du}}{\left({u}+\mathrm{1}\right)\left({u}−\mathrm{1}\right)} \\ $$$$=\int_{\sqrt{\mathrm{2}}+\mathrm{1}} ^{+\infty} \left(\frac{\mathrm{1}}{{u}−\mathrm{1}}−\frac{\mathrm{1}}{{u}+\mathrm{1}}\right){du} \\ $$$$=\left[{ln}\mid\frac{{u}−\mathrm{1}}{{u}+\mathrm{1}}\mid\right]_{\sqrt{\mathrm{2}}+\mathrm{1}} ^{+\infty} ={ln}\mid\frac{\sqrt{\mathrm{2}}+\mathrm{2}}{\sqrt{\mathrm{2}}}\mid= \\ $$$${L}={ln}\left(\sqrt{\mathrm{2}}+\mathrm{1}\right) \\ $$$$ \\ $$
Answered by ajfour last updated on 31/May/18

$${let}\:\:\:{t}=\mathrm{tan}\:\theta\:\:;\:{then} \\ $$$${I}=\int_{\pi/\mathrm{4}} ^{\:\:\pi/\mathrm{2}} \:\frac{\mathrm{sec}\:^{\mathrm{2}} \theta{d}\theta}{\left(\mathrm{tan}\:\theta\right)\mathrm{sec}\:\theta} \\ $$$${I}=\int_{\pi/\mathrm{4}} ^{\:\:\pi/\mathrm{2}} \:\mathrm{cosec}\:\theta{d}\theta \\ $$$$\:\:\:=\mathrm{ln}\:\mid\frac{\mathrm{cosec}\:\left(\pi/\mathrm{2}\right)−\mathrm{cot}\:\left(\pi/\mathrm{2}\right)}{\mathrm{cosec}\:\left(\pi/\mathrm{4}\right)−\mathrm{cot}\:\left(\pi/\mathrm{4}\right)}\mid \\ $$$$\:\:\:=\mathrm{ln}\:\left(\frac{\mathrm{1}}{\sqrt{\mathrm{2}}−\mathrm{1}}\right)\:=\:\mathrm{ln}\:\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\:. \\ $$$$\: \\ $$
