
Question and Answers Forum
Question Number 36190 by prof Abdo imad last updated on 30/May/18
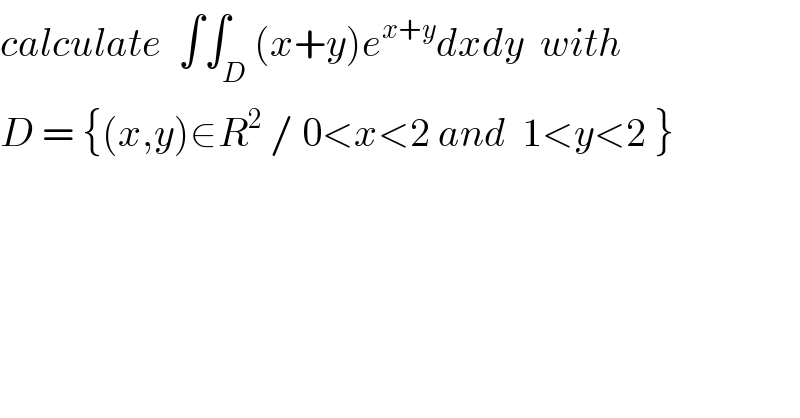
Commented bymaxmathsup by imad last updated on 20/Aug/18
![I =∫_1 ^2 (∫_0 ^2 (x+y)e^(x+y) dx)dy =∫_1 ^2 A(y)dy with A(y)=∫_0 ^2 (x+y)e^(x+y) dx A(y) = e^(y ) ∫_0 ^2 (x+y)e^x dx =e^y ∫_0 ^2 (xe^x +y e^x )ex =e^y { ∫_0 ^2 xe^x dx +y ∫_0 ^2 e^x dx} but ∫_0 ^2 e^x dx =[e^x ]_0 ^2 =e^2 −1 and by parts ∫_0 ^2 x e^x dx =[x e^x ]_0 ^2 −∫_0 ^2 e^x dx =2e^2 −e^2 +1 =e^2 +1 ⇒A(y)=e^y (e^2 +1+y(e^2 −1)) =(e^2 +1)e^y +(e^2 −1)y e^y ⇒ I = ∫_1 ^2 { (e^2 +1)e^y +(e^2 −1)ye^y )dy =(e^2 +1)∫_1 ^2 e^y dy +(e^2 −1) ∫_1 ^2 y e^y dy but ∫_1 ^2 e^y dy =e^2 −e and ∫_1 ^2 y e^y dy =[y e^y ]_1 ^2 −∫_1 ^2 e^y dy =2e^2 −e −e^2 +e =e^2 ⇒ I =(e^2 +1)(e^2 −e) +(e^2 −1)e^2 I =e^4 −e^3 +e^2 −e +e^4 −e^2 ⇒ I =2e^(4 ) −e^3 .](Q42233.png)
| ||
Question and Answers Forum | ||
Question Number 36190 by prof Abdo imad last updated on 30/May/18 | ||
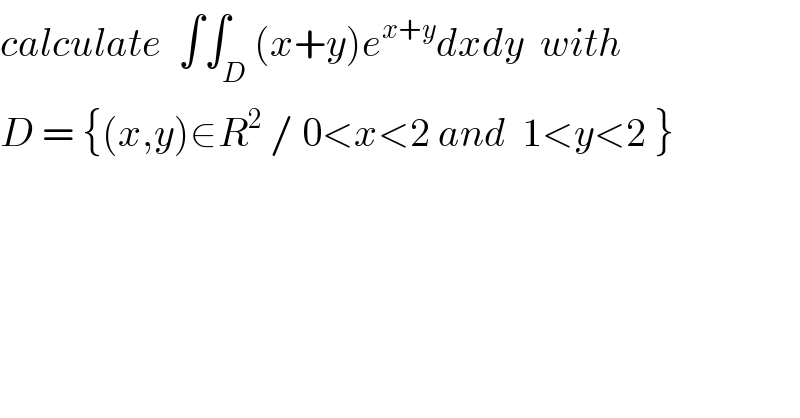 | ||
Commented bymaxmathsup by imad last updated on 20/Aug/18 | ||
![I =∫_1 ^2 (∫_0 ^2 (x+y)e^(x+y) dx)dy =∫_1 ^2 A(y)dy with A(y)=∫_0 ^2 (x+y)e^(x+y) dx A(y) = e^(y ) ∫_0 ^2 (x+y)e^x dx =e^y ∫_0 ^2 (xe^x +y e^x )ex =e^y { ∫_0 ^2 xe^x dx +y ∫_0 ^2 e^x dx} but ∫_0 ^2 e^x dx =[e^x ]_0 ^2 =e^2 −1 and by parts ∫_0 ^2 x e^x dx =[x e^x ]_0 ^2 −∫_0 ^2 e^x dx =2e^2 −e^2 +1 =e^2 +1 ⇒A(y)=e^y (e^2 +1+y(e^2 −1)) =(e^2 +1)e^y +(e^2 −1)y e^y ⇒ I = ∫_1 ^2 { (e^2 +1)e^y +(e^2 −1)ye^y )dy =(e^2 +1)∫_1 ^2 e^y dy +(e^2 −1) ∫_1 ^2 y e^y dy but ∫_1 ^2 e^y dy =e^2 −e and ∫_1 ^2 y e^y dy =[y e^y ]_1 ^2 −∫_1 ^2 e^y dy =2e^2 −e −e^2 +e =e^2 ⇒ I =(e^2 +1)(e^2 −e) +(e^2 −1)e^2 I =e^4 −e^3 +e^2 −e +e^4 −e^2 ⇒ I =2e^(4 ) −e^3 .](Q42233.png) | ||