
Question and Answers Forum
Question Number 36191 by prof Abdo imad last updated on 30/May/18
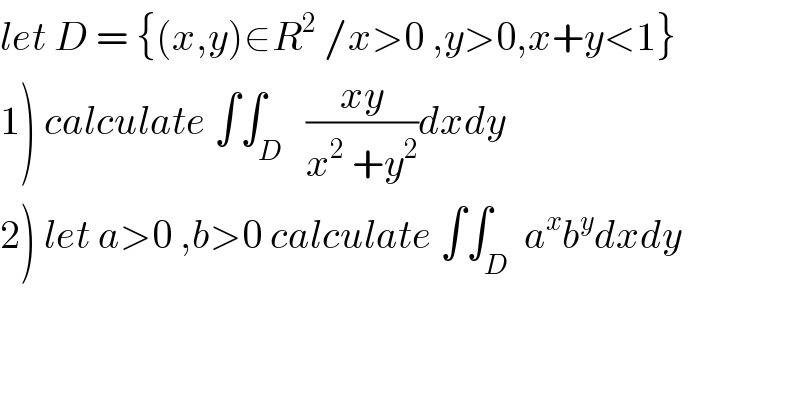
Commented bymaxmathsup by imad last updated on 26/Aug/18
![polar coordinates changement x =rcosθ and y =rsinθ x>0 and y>0 ⇒ 0<θ<(π/2) and x+y <1 ⇒ r(cosθ +sinθ)<1 ⇒ 0<r<(1/(cosθ +sinθ)) ∫∫_D ((xy)/(x^2 +y^2 ))dxdy = ∫_0 ^(π/2) (∫_0 ^(1/(cosθ+sinθ)) ((r^2 cosθsinθ)/r^2 ) rdr)dθ =∫_0 ^(π/2) ( ∫_0 ^(1/(cosθ +sinθ)) rdr)cosθ sinθ dθ but ∫_0 ^(1/(cosθ +sinθ)) rdr =[(r^2 /2)]_0 ^(1/(cosθ +sinθ)) =(1/(2(cosθ +sinθ)^2 )) =(1/(2(1+2sinθ cosθ))) ⇒ I = ∫_0 ^(π/2) ((cosθ sinθ)/(2(1+2sinθ cosθ)))dθ =(1/4) ∫_0 ^(π/2) ((sin(2θ))/(1+sin(2θ)))dθ =_(2θ =t) (1/4) ∫_0 ^π ((sint)/(1+sint)) (dt/2) =(1/8) ∫_0 ^π ((1+sint −1)/(1+sint))dt =(π/8) −(1/8) ∫_0 ^π (dt/(1+sint)) chang. tan((t/2)) =u give ∫_0 ^π (dt/(1+sint)) = ∫_0 ^∞ (1/(1+((2u)/(1+u^2 )))) ((2du)/(1+u^2 )) =2 ∫_0 ^∞ (du/(1+u^2 +2u)) =2 ∫_0 ^∞ (du/((u+1)^2 )) =2[−(1/(u+1))]_0 ^(+∞) = 2 ⇒ I =(π/8) −(1/4) .](Q42485.png)
| ||
Question and Answers Forum | ||
Question Number 36191 by prof Abdo imad last updated on 30/May/18 | ||
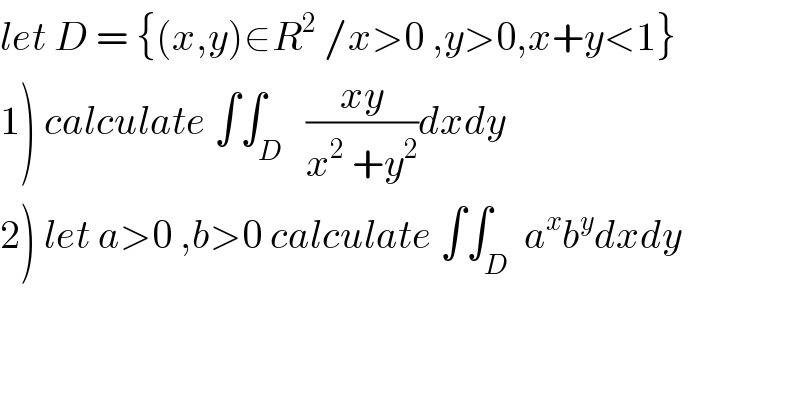 | ||
Commented bymaxmathsup by imad last updated on 26/Aug/18 | ||
![polar coordinates changement x =rcosθ and y =rsinθ x>0 and y>0 ⇒ 0<θ<(π/2) and x+y <1 ⇒ r(cosθ +sinθ)<1 ⇒ 0<r<(1/(cosθ +sinθ)) ∫∫_D ((xy)/(x^2 +y^2 ))dxdy = ∫_0 ^(π/2) (∫_0 ^(1/(cosθ+sinθ)) ((r^2 cosθsinθ)/r^2 ) rdr)dθ =∫_0 ^(π/2) ( ∫_0 ^(1/(cosθ +sinθ)) rdr)cosθ sinθ dθ but ∫_0 ^(1/(cosθ +sinθ)) rdr =[(r^2 /2)]_0 ^(1/(cosθ +sinθ)) =(1/(2(cosθ +sinθ)^2 )) =(1/(2(1+2sinθ cosθ))) ⇒ I = ∫_0 ^(π/2) ((cosθ sinθ)/(2(1+2sinθ cosθ)))dθ =(1/4) ∫_0 ^(π/2) ((sin(2θ))/(1+sin(2θ)))dθ =_(2θ =t) (1/4) ∫_0 ^π ((sint)/(1+sint)) (dt/2) =(1/8) ∫_0 ^π ((1+sint −1)/(1+sint))dt =(π/8) −(1/8) ∫_0 ^π (dt/(1+sint)) chang. tan((t/2)) =u give ∫_0 ^π (dt/(1+sint)) = ∫_0 ^∞ (1/(1+((2u)/(1+u^2 )))) ((2du)/(1+u^2 )) =2 ∫_0 ^∞ (du/(1+u^2 +2u)) =2 ∫_0 ^∞ (du/((u+1)^2 )) =2[−(1/(u+1))]_0 ^(+∞) = 2 ⇒ I =(π/8) −(1/4) .](Q42485.png) | ||