
Question Number 36193 by prof Abdo imad last updated on 30/May/18
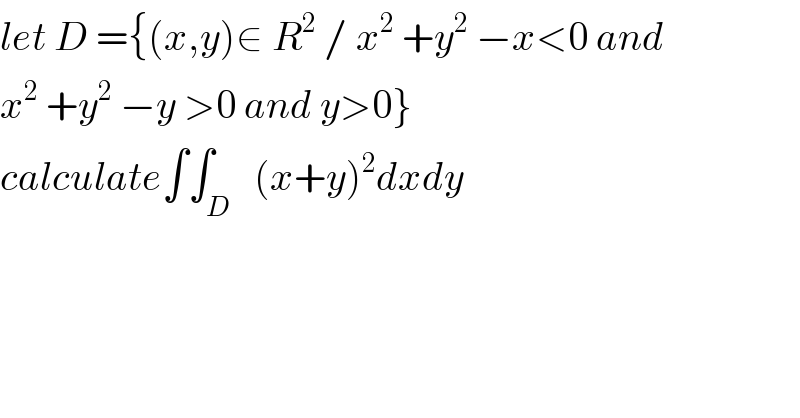
$${let}\:{D}\:=\left\{\left({x},{y}\right)\in\:{R}^{\mathrm{2}} \:/\:{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} \:−{x}<\mathrm{0}\:{and}\right. \\ $$ $$\left.{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} \:−{y}\:>\mathrm{0}\:{and}\:{y}>\mathrm{0}\right\} \\ $$ $${calculate}\int\int_{{D}} \:\:\left({x}+{y}\right)^{\mathrm{2}} {dxdy} \\ $$
Commented bymaxmathsup by imad last updated on 15/Aug/18
![changement x=r cosθ and y =r sinθ give x^2 +y^2 −x <0 ⇒r^2 −rcosθ <0 ⇒r<cosθ x^2 +y^2 −y>0 ⇒r^2 −r sinθ >0 ⇒sinθ<r ⇒ sinθ<r<cosθ ∫∫_D (x+y)^2 dxdy = ∫∫_D (x^2 +y^2 +2xy)dxdy = ∫_0 ^(2π) (∫_(sinθ) ^(cosθ) (r^2 +2r^2 cosθ sinθ)rdr)dθ =∫_0 ^(2π) ( ∫_(sinθ) ^(cosθ) r^3 dr +∫_(sinθ) ^(cosθ) 2r^3 sinθ coθ dr)dθ =(1/4)∫_0 ^(2π) (cos^4 θ−sin^4 θ)dθ +(1/2) ∫_0 ^(2π) sinθ cosθ(cos^4 θ −sin^4 θ)dθ =(1/4) ∫_0 ^(2π) cos(2θ)dθ + (1/4) ∫_0 ^(2π) sinθ cosθ(cos^2 θ −sin^2 θ)dθ =0 +(1/4) ∫_0 ^(2π) sinθ cos^3 θdθ −(1/4) ∫_0 ^(2π) cosθ sin^3 θ =−(1/(16)) [cos^4 θ]_0 ^(2π) −(1/(16))[sin^4 θ]_0 ^(2π) =0 ⇒ I =0](Q41934.png)
$${changement}\:\:{x}={r}\:{cos}\theta\:\:{and}\:{y}\:={r}\:{sin}\theta\:\:{give} \\ $$ $${x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} −{x}\:<\mathrm{0}\:\Rightarrow{r}^{\mathrm{2}} \:−{rcos}\theta\:<\mathrm{0}\:\Rightarrow{r}<{cos}\theta \\ $$ $${x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} −{y}>\mathrm{0}\:\Rightarrow{r}^{\mathrm{2}} −{r}\:{sin}\theta\:>\mathrm{0}\:\Rightarrow{sin}\theta<{r}\:\Rightarrow\:{sin}\theta<{r}<{cos}\theta \\ $$ $$\int\int_{{D}} \left({x}+{y}\right)^{\mathrm{2}} {dxdy}\:=\:\int\int_{{D}} \left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \:+\mathrm{2}{xy}\right){dxdy} \\ $$ $$=\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\left(\int_{{sin}\theta} ^{{cos}\theta} \:\left({r}^{\mathrm{2}} \:+\mathrm{2}{r}^{\mathrm{2}} {cos}\theta\:{sin}\theta\right){rdr}\right){d}\theta \\ $$ $$=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\left(\:\int_{{sin}\theta} ^{{cos}\theta} {r}^{\mathrm{3}} {dr}\:\:+\int_{{sin}\theta} ^{{cos}\theta} \:\mathrm{2}{r}^{\mathrm{3}} {sin}\theta\:{co}\theta\:{dr}\right){d}\theta \\ $$ $$=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\left({cos}^{\mathrm{4}} \theta−{sin}^{\mathrm{4}} \theta\right){d}\theta\:\:\:+\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} {sin}\theta\:{cos}\theta\left({cos}^{\mathrm{4}} \theta\:−{sin}^{\mathrm{4}} \theta\right){d}\theta \\ $$ $$=\frac{\mathrm{1}}{\mathrm{4}}\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:{cos}\left(\mathrm{2}\theta\right){d}\theta\:\:+\:\frac{\mathrm{1}}{\mathrm{4}}\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} {sin}\theta\:{cos}\theta\left({cos}^{\mathrm{2}} \theta\:−{sin}^{\mathrm{2}} \theta\right){d}\theta \\ $$ $$=\mathrm{0}\:+\frac{\mathrm{1}}{\mathrm{4}}\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} {sin}\theta\:{cos}^{\mathrm{3}} \theta{d}\theta\:−\frac{\mathrm{1}}{\mathrm{4}}\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:{cos}\theta\:{sin}^{\mathrm{3}} \theta \\ $$ $$=−\frac{\mathrm{1}}{\mathrm{16}}\:\left[{cos}^{\mathrm{4}} \theta\right]_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:−\frac{\mathrm{1}}{\mathrm{16}}\left[{sin}^{\mathrm{4}} \theta\right]_{\mathrm{0}} ^{\mathrm{2}\pi} \:=\mathrm{0}\:\Rightarrow\:{I}\:=\mathrm{0} \\ $$
