
Question and Answers Forum
Question Number 36218 by Rio Mike last updated on 30/May/18
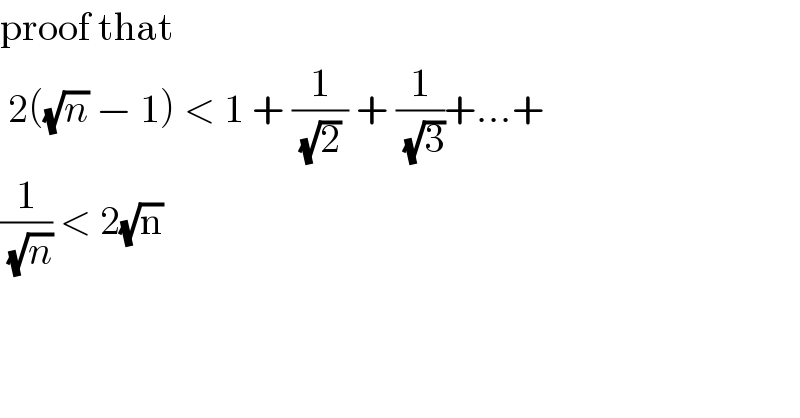
Commented byabdo mathsup 649 cc last updated on 30/May/18
![the function f(x)= (1/(√x)) is decreasing on ]0,+∞[so ∫_k ^(k+1) f(t)dt≤ f(k) ≤ ∫_(k−1) ^k f(t)dt ⇒ Σ_(k=1) ^n ∫_k ^(k+1) f(t)dt ≤ Σ_(k=1) ^n f(k) ≤ Σ_(k=1) ^n ∫_(n−1) ^n f(t)dt ⇒ ∫_1 ^(n+1) (dt/(√t)) ≤ 1 +(1/(√2)) +...+(1/(√n))≤ ∫_0 ^n (dt/(√t)) ⇒ [2(√t)]_1 ^(n+1) ≤ 1 +(1/(√2)) +....+(1/(√n))−≤ [2.(√n)]_0 ^n ⇒ 2{(√(n+1)) −1 }≤ 1 +(1/2) +...+(1/(√n)) ≤ 2(√n) but (√n_ ) ≤.(√(n+1)) ⇒ 2{(√n)−1} ≤ 1+(1/2) +....+(1/(√n)) ≤ 2(√n) .](Q36247.png)
| ||
Question and Answers Forum | ||
Question Number 36218 by Rio Mike last updated on 30/May/18 | ||
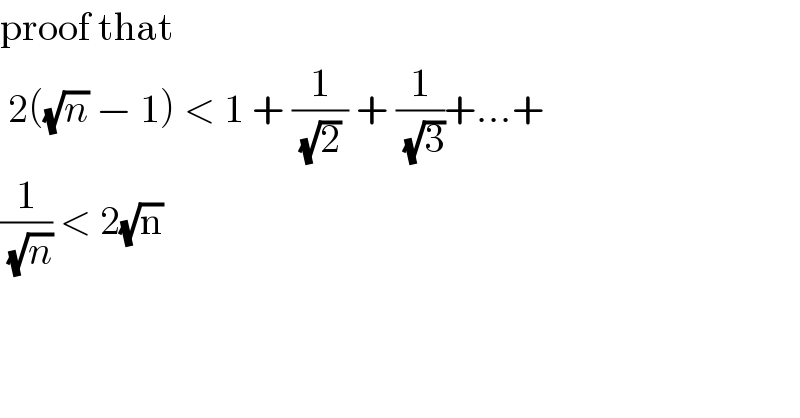 | ||
Commented byabdo mathsup 649 cc last updated on 30/May/18 | ||
![the function f(x)= (1/(√x)) is decreasing on ]0,+∞[so ∫_k ^(k+1) f(t)dt≤ f(k) ≤ ∫_(k−1) ^k f(t)dt ⇒ Σ_(k=1) ^n ∫_k ^(k+1) f(t)dt ≤ Σ_(k=1) ^n f(k) ≤ Σ_(k=1) ^n ∫_(n−1) ^n f(t)dt ⇒ ∫_1 ^(n+1) (dt/(√t)) ≤ 1 +(1/(√2)) +...+(1/(√n))≤ ∫_0 ^n (dt/(√t)) ⇒ [2(√t)]_1 ^(n+1) ≤ 1 +(1/(√2)) +....+(1/(√n))−≤ [2.(√n)]_0 ^n ⇒ 2{(√(n+1)) −1 }≤ 1 +(1/2) +...+(1/(√n)) ≤ 2(√n) but (√n_ ) ≤.(√(n+1)) ⇒ 2{(√n)−1} ≤ 1+(1/2) +....+(1/(√n)) ≤ 2(√n) .](Q36247.png) | ||