Math Question and Answers


Question and Answers Forum

All Questions Topic List
Geometry Questions
Previous in All Question Next in All Question
Previous in Geometry Next in Geometry
Question Number 36270 by ajfour last updated on 30/May/18

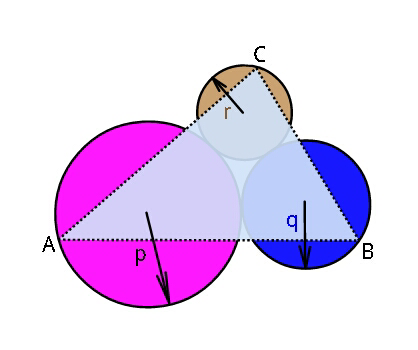
Commented by ajfour last updated on 30/May/18

$F i n d m a x i m u m a r e a o f a t r i a n g l e$ $w h e n i t s v e r t i c e s l i e o n t h e$ $c i r u m f e r e n c e o f t h r e e c i r c l e s .$ $(A s s h o w n i n f i g . t h e c i r c l e s$ $t o u c h e a c h o t h e r) .$
Commented by tanmay.chaudhury50@gmail.com last updated on 31/May/18

$i h a v e d e l e t e d t h e p o s t . . . y e s i w a s w r o n g$
Commented by MJS last updated on 31/May/18

$anyway thank you for all the input, {it}^{'} s$ $good to have many people with many$ $different points of view$
Commented by ajfour last updated on 31/May/18

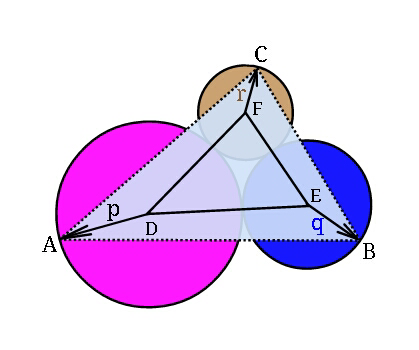
Commented by ajfour last updated on 31/May/18

$m r W S i r, i m a g a i n w i s h i n g$ $y o u r c o o p e r a t i o n . . .$
Commented by ajfour last updated on 31/May/18

$l e t D E b e x - a x i s w i t h D a s o r i g i n .$ $l e t ∠ F D E = α$ $A \equiv (x_{1}, y_{1}), B \equiv (x_{2}, y_{2}), C \equiv (x_{3}, y_{3})$ $x_{1}^{2} + y_{1}^{2} = p^{2}$ ${(x_{2} - p - q)}^{2} + y_{2}^{2} = q^{2}$ ${[x_{3} - (p + r) \cos α]}^{2} + [y_{3} - (p + r) \sin α] = r^{2}$ $△ = \frac{1}{2} \| \begin{matrix} x_{1} & y_{1} & 1 \\ x_{2} & y_{2} & 1 \\ x_{3} & y_{3} & 1 \end{matrix} \| w i t h$ $\frac{\partial △}{\partial x_{1}} = 0, \frac{\partial △}{\partial x_{2}} = 0, \frac{\partial △}{\partial x_{3}} = 0$ $\Rightarrow \| \begin{matrix} 1 & - \frac{x_{1}}{y_{1}} & 1 \\ x_{2} & y_{2} & 1 \\ x_{3} & y_{3} & 1 \end{matrix} \| = 0$ $\Rightarrow (y_{2} - y_{3}) + \frac{x_{1}}{y_{1}} (x_{2} - x_{3}) + (x_{2} y_{3} - x_{3} y_{2}) = 0$ $s i m i l a r l y t w o m o r e e q u a t i o n s$ $f o r \frac{\partial △}{\partial x_{2}} = 0, \frac{\partial △}{\partial x_{3}} = 0 .$ $u s i n g t h e s e s i x e q u a t i o n s w e f i n d$ $(x_{i}, y_{i}) a n d t h u s △_{m a x} .$
Commented by MrW3 last updated on 11/Jun/18
Great!
Commented by MrW3 last updated on 12/Jun/18

$t h e t r i a n g l e w i t h t h e m a x . a r e a s h o u l d$ $b e t h a t o n e w h i c h f u l f i l l s :$ $t a n g e n t a t A i s p a r a l l e l t o B C$ $t a n g e n t a t B i s p a r a l l e l t o C A$ $t a n g e n t a t C i s p a r a l l e l t o A B$
	Answered by MJS last updated on 02/Jun/18

	$in A the tangent must be parallel to the line$ $M_{q} M_{r}, same goes for B & M_{p} M_{r} and C & M_{p} M_{q}$ $I came to this conclusion by calculating it for$ $p = q = r and then reducing r . I tried to find the$ $formulas but {couldn}^{'} t handle them . with given$ $values for p, q, r {it}^{'} s easy to calculate and see$ $that changing one of the verticles A, B, C$ $(use △ θ) by any small value will decrease the$ $area .$ $I^{'} ll try to show . . .$
	Commented by MrW3 last updated on 12/Jun/18

	$I t h i n k y o u r c o n c l u s i o n i s n o t c o r r e c t, s i r .$ $T h e t a n g e n t a t A s h o u l d b e p a r a l l e l t o t h e$ $l i n e B C, n o t t o t h e l i n e M_{q} M_{r}, e t c .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum