Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 36406 by abdo mathsup 649 cc last updated on 01/Jun/18

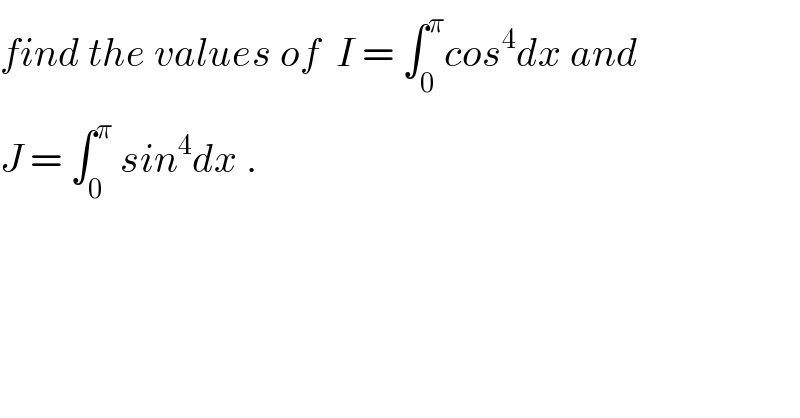
find the values of I = ∫_0 ^π cos^4 dx and J = ∫_0 ^π sin^4 dx .

$${find}\:{the}\:{values}\:{of}\:\:{I}\:=\:\int_{\mathrm{0}} ^{\pi} {cos}^{\mathrm{4}} {dx}\:{and} \\ $$$${J}\:=\:\int_{\mathrm{0}} ^{\pi} \:{sin}^{\mathrm{4}} {dx}\:. \\ $$

Commented by abdo.msup.com last updated on 05/Jun/18

we have I +J =∫_0 ^π (cos^4 x +sin^4 x)dx =∫_0 ^π {(cos^2 x +sin^2 x)^2 −2cos^2 xsin^2 x}dx =π −2 ∫_0 ^π (1/4)(sin(2x))^2 dx =π −(1/2) ∫_0 ^π ((1−cos(4x))/2)dx =π −(π/4) + (1/(16))[sin(4x)]_0 ^π =((3π)/4) also I −J = ∫_0 ^π (cos^4 x −sin^4 x)dx = ∫_0 ^π cos^2 x −sin^2 x dx = ∫_0 ^π cos(2x)dx=(1/2)[ sin(2x)]_0 ^π =0 so I =J ⇒ 2I = ((3π)/4) ⇒ I =((3π)/8) and J =((3π)/8)

$${we}\:{have}\:\:{I}\:+{J}\:=\int_{\mathrm{0}} ^{\pi} \:\left({cos}^{\mathrm{4}} {x}\:+{sin}^{\mathrm{4}} {x}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\pi} \:\:\left\{\left({cos}^{\mathrm{2}} {x}\:+{sin}^{\mathrm{2}} {x}\right)^{\mathrm{2}} \:−\mathrm{2}{cos}^{\mathrm{2}} {xsin}^{\mathrm{2}} {x}\right\}{dx} \\ $$$$=\pi\:−\mathrm{2}\:\int_{\mathrm{0}} ^{\pi} \:\frac{\mathrm{1}}{\mathrm{4}}\left({sin}\left(\mathrm{2}{x}\right)\right)^{\mathrm{2}} {dx} \\ $$$$=\pi\:−\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\pi} \:\:\frac{\mathrm{1}−{cos}\left(\mathrm{4}{x}\right)}{\mathrm{2}}{dx} \\ $$$$=\pi\:−\frac{\pi}{\mathrm{4}}\:+\:\frac{\mathrm{1}}{\mathrm{16}}\left[{sin}\left(\mathrm{4}{x}\right)\right]_{\mathrm{0}} ^{\pi} \:=\frac{\mathrm{3}\pi}{\mathrm{4}}\:{also} \\ $$$${I}\:−{J}\:=\:\int_{\mathrm{0}} ^{\pi} \:\left({cos}^{\mathrm{4}} {x}\:−{sin}^{\mathrm{4}} {x}\right){dx} \\ $$$$=\:\int_{\mathrm{0}} ^{\pi} \:{cos}^{\mathrm{2}} {x}\:−{sin}^{\mathrm{2}} {x}\:{dx} \\ $$$$=\:\int_{\mathrm{0}} ^{\pi} \:\:{cos}\left(\mathrm{2}{x}\right){dx}=\frac{\mathrm{1}}{\mathrm{2}}\left[\:{sin}\left(\mathrm{2}{x}\right)\right]_{\mathrm{0}} ^{\pi} =\mathrm{0}\:{so} \\ $$$${I}\:={J}\:\Rightarrow\:\mathrm{2}{I}\:=\:\frac{\mathrm{3}\pi}{\mathrm{4}}\:\Rightarrow\:{I}\:=\frac{\mathrm{3}\pi}{\mathrm{8}}\:{and}\:{J}\:=\frac{\mathrm{3}\pi}{\mathrm{8}} \\ $$$$ \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 01/Jun/18

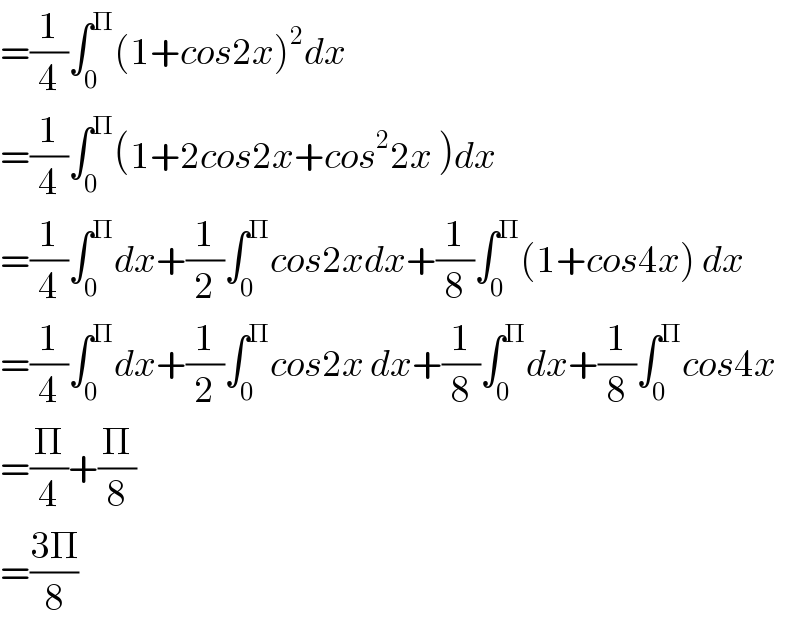
=(1/4)∫_0 ^Π (1+cos2x)^2 dx =(1/4)∫_0 ^Π (1+2cos2x+cos^2 2x )dx =(1/4)∫_0 ^Π dx+(1/2)∫_0 ^Π cos2xdx+(1/8)∫_0 ^Π (1+cos4x) dx =(1/4)∫_0 ^Π dx+(1/2)∫_0 ^Π cos2x dx+(1/8)∫_0 ^Π dx+(1/8)∫_0 ^Π cos4x =(Π/4)+(Π/8) =((3Π)/8)

$$=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\Pi} \left(\mathrm{1}+{cos}\mathrm{2}{x}\right)^{\mathrm{2}} {dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\Pi} \left(\mathrm{1}+\mathrm{2}{cos}\mathrm{2}{x}+{cos}^{\mathrm{2}} \mathrm{2}{x}\:\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\Pi} {dx}+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\Pi} {cos}\mathrm{2}{xdx}+\frac{\mathrm{1}}{\mathrm{8}}\int_{\mathrm{0}} ^{\Pi} \left(\mathrm{1}+{cos}\mathrm{4}{x}\right)\:{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\Pi} {dx}+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\Pi} {cos}\mathrm{2}{x}\:{dx}+\frac{\mathrm{1}}{\mathrm{8}}\int_{\mathrm{0}} ^{\Pi} {dx}+\frac{\mathrm{1}}{\mathrm{8}}\int_{\mathrm{0}} ^{\Pi} {cos}\mathrm{4}{x} \\ $$$$=\frac{\Pi}{\mathrm{4}}+\frac{\Pi}{\mathrm{8}} \\ $$$$=\frac{\mathrm{3}\Pi}{\mathrm{8}} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 01/Jun/18

j=∫_0 ^(Π() (((1−cos2x)/2))^2 =(1/4)∫_0 ^Π 1−2cos2x+((1+cos4x)/2)dx =(1/4)∫_0 ^Π dx−(1/2)∫_0 ^Π cos2xdx+(1/8)∫_0 ^Π dx+(1/8)∫_0 ^Π cos4x =(Π/4)+(Π/8)=((3Π)/8)

$${j}=\int_{\mathrm{0}} ^{\Pi\left(\right.} \left(\frac{\mathrm{1}−{cos}\mathrm{2}{x}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\Pi} \mathrm{1}−\mathrm{2}{cos}\mathrm{2}{x}+\frac{\mathrm{1}+{cos}\mathrm{4}{x}}{\mathrm{2}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\Pi} {dx}−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\Pi} {cos}\mathrm{2}{xdx}+\frac{\mathrm{1}}{\mathrm{8}}\int_{\mathrm{0}} ^{\Pi} {dx}+\frac{\mathrm{1}}{\mathrm{8}}\int_{\mathrm{0}} ^{\Pi} {cos}\mathrm{4}{x} \\ $$$$=\frac{\Pi}{\mathrm{4}}+\frac{\Pi}{\mathrm{8}}=\frac{\mathrm{3}\Pi}{\mathrm{8}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com