Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 36419 by abdo.msup.com last updated on 01/Jun/18

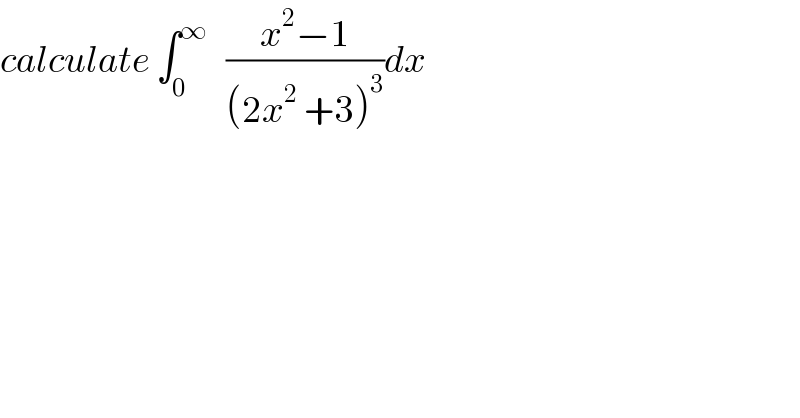
calculate ∫_0 ^∞ ((x^2 −1)/((2x^2 +3)^3 ))dx

$${calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{x}^{\mathrm{2}} −\mathrm{1}}{\left(\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{3}\right)^{\mathrm{3}} }{dx} \\ $$

Commented by abdo.msup.com last updated on 04/Jun/18

we have I = ∫_0 ^∞ ((x^2 −1)/(8( x^2 +(3/2))^3 ))dx 8 I = ∫_0 ^∞ ((x^2 −1)/((x^2 +(3/2))^3 ))dx 16 I = ∫_(−∞) ^(+∞) ((x^2 −1)/((x^2 +(3/2))^3 ))dx let consider the complex function ϕ(z)= ((z^2 −1)/((z^2 +(3/2))^3 )) we have ϕ(z) = ((z^2 −1)/((z −i(√(3/2)))^3 (z +i(√(3/2)))^3 )) the?roots of ϕ are i(√(3/2)) and −i(√(3/2)) (triples) so ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ Res( ϕ ,i(√(3/2))) Res(ϕ,i(√(3/2)))=lim_(z→i(√(3/2))) (1/((3−1)!)){(z−i(√(3/2)))^3 ϕ(z)}^((2)) =lim_(z→i(√(3/2))) (1/2){ ((z^2 −1)/((z+i(√(3/2)))^3 ))}^((2)) =lim_(z→i(√(3/2))) (1/2){ ((2z(z+i(√(3/2)))^3 −3(z+i(√(3/2)))^2 (z^2 −1))/((z+i(√(3/2)))^6 ))}^((1)) =lim_(z→i(√(3/2))) (1/2){ ((2z(z +i(√(3/2))) −3(z^2 −1))/((z +i(√(3/2)))^4 ))}^((1)) ...

$${we}\:{have}\:{I}\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{x}^{\mathrm{2}} −\mathrm{1}}{\mathrm{8}\left(\:{x}^{\mathrm{2}} \:+\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{3}} }{dx} \\ $$$$\mathrm{8}\:{I}\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\frac{{x}^{\mathrm{2}} \:−\mathrm{1}}{\left({x}^{\mathrm{2}} \:+\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{3}} }{dx} \\ $$$$\mathrm{16}\:{I}\:=\:\int_{−\infty} ^{+\infty} \:\:\frac{{x}^{\mathrm{2}} \:−\mathrm{1}}{\left({x}^{\mathrm{2}} \:+\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{3}} }{dx}\:{let}\:{consider} \\ $$$${the}\:{complex}\:{function} \\ $$$$\varphi\left({z}\right)=\:\frac{{z}^{\mathrm{2}} \:−\mathrm{1}}{\left({z}^{\mathrm{2}} \:+\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{3}} }\:\:{we}\:{have}\: \\ $$$$\varphi\left({z}\right)\:=\:\frac{{z}^{\mathrm{2}} \:−\mathrm{1}}{\left({z}\:−{i}\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\right)^{\mathrm{3}} \left({z}\:+{i}\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\right)^{\mathrm{3}} } \\ $$$${the}?{roots}\:{of}\:\varphi\:{are}\:{i}\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\:\:{and}\:−{i}\sqrt{\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$$\left({triples}\right)\:{so} \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:{Res}\left(\:\varphi\:,{i}\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\right) \\ $$$${Res}\left(\varphi,{i}\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\right)={lim}_{{z}\rightarrow{i}\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}} \:\:\:\frac{\mathrm{1}}{\left(\mathrm{3}−\mathrm{1}\right)!}\left\{\left({z}−{i}\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\right)^{\mathrm{3}} \varphi\left({z}\right)\right\}^{\left(\mathrm{2}\right)} \\ $$$$={lim}_{{z}\rightarrow{i}\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}} \:\:\frac{\mathrm{1}}{\mathrm{2}}\left\{\:\frac{{z}^{\mathrm{2}} \:−\mathrm{1}}{\left({z}+{i}\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\right)^{\mathrm{3}} }\right\}^{\left(\mathrm{2}\right)} \\ $$$$={lim}_{{z}\rightarrow{i}\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}} \:\:\frac{\mathrm{1}}{\mathrm{2}}\left\{\:\frac{\mathrm{2}{z}\left({z}+{i}\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\right)^{\mathrm{3}} \:−\mathrm{3}\left({z}+{i}\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\right)^{\mathrm{2}} \left({z}^{\mathrm{2}} \:−\mathrm{1}\right)}{\left({z}+{i}\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\right)^{\mathrm{6}} }\right\}^{\left(\mathrm{1}\right)} \\ $$$$={lim}_{{z}\rightarrow{i}\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}} \:\frac{\mathrm{1}}{\mathrm{2}}\left\{\:\frac{\mathrm{2}{z}\left({z}\:+{i}\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\right)\:−\mathrm{3}\left({z}^{\mathrm{2}} −\mathrm{1}\right)}{\left({z}\:+{i}\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\right)^{\mathrm{4}} }\right\}^{\left(\mathrm{1}\right)} \\ $$$$... \\ $$

Commented by abdo.msup.com last updated on 04/Jun/18

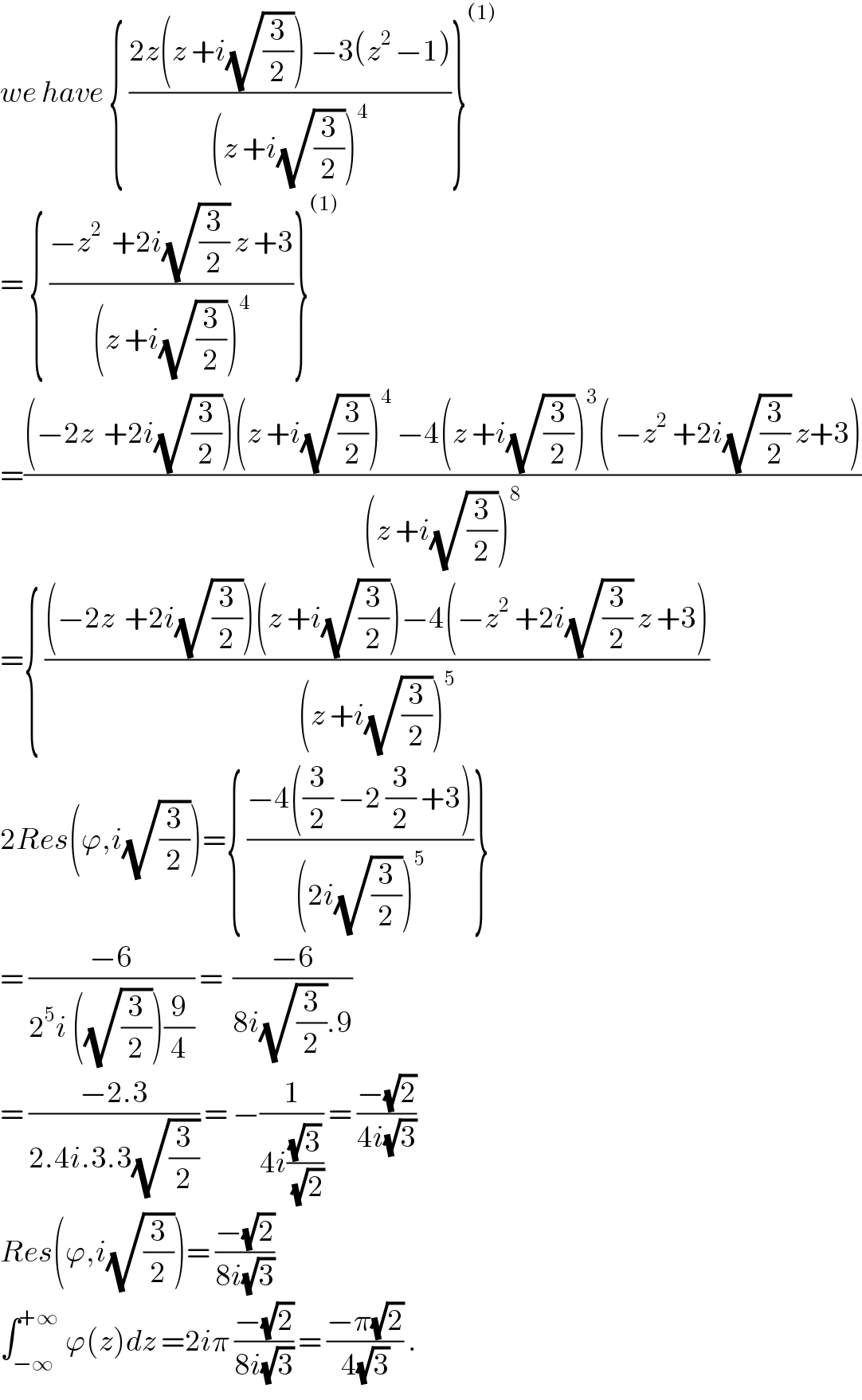
we have { ((2z(z +i(√(3/2))) −3(z^(2 ) −1))/((z +i(√(3/2)))^4 ))}^((1)) = { ((−z^2 +2i(√(3/2)) z +3)/((z +i(√(3/2)))^4 ))}^((1)) =(((−2z +2i(√(3/2)))(z +i(√(3/2)))^4 −4(z +i(√(3/2)))^3 ( −z^2 +2i(√(3/2)) z+3))/((z +i(√(3/2)))^8 )) ={ (((−2z +2i(√(3/2)))(z +i(√(3/2)))−4(−z^2 +2i(√(3/2)) z +3))/((z +i(√(3/2)))^5 )) 2Res(ϕ,i(√(3/2)))={ ((−4((3/2) −2 (3/2) +3))/((2i(√(3/2)))^5 ))} = ((−6)/(2^5 i ((√(3/2)))(9/4))) = ((−6)/(8i(√(3/2)).9)) = ((−2.3)/(2.4i.3.3(√(3/2)))) = −(1/(4i((√3)/(√2)))) = ((−(√2))/(4i(√3))) Res(ϕ,i(√(3/2)))= ((−(√2))/(8i(√3))) ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ ((−(√2))/(8i(√3))) = ((−π(√2))/(4(√3))) .

$${we}\:{have}\:\left\{\:\frac{\mathrm{2}{z}\left({z}\:+{i}\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\right)\:−\mathrm{3}\left({z}^{\mathrm{2}\:} −\mathrm{1}\right)}{\left({z}\:+{i}\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\right)^{\mathrm{4}} }\right\}^{\left(\mathrm{1}\right)} \\ $$$$=\:\left\{\:\frac{−{z}^{\mathrm{2}} \:\:+\mathrm{2}{i}\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\:{z}\:+\mathrm{3}}{\left({z}\:+{i}\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\right)^{\mathrm{4}} }\right\}^{\left(\mathrm{1}\right)} \\ $$$$=\frac{\left(−\mathrm{2}{z}\:\:+\mathrm{2}{i}\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\right)\left({z}\:+{i}\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\right)^{\mathrm{4}} \:−\mathrm{4}\left({z}\:+{i}\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\right)^{\mathrm{3}} \left(\:−{z}^{\mathrm{2}} \:+\mathrm{2}{i}\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\:{z}+\mathrm{3}\right)}{\left({z}\:+{i}\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\right)^{\mathrm{8}} } \\ $$$$=\left\{\:\frac{\left(−\mathrm{2}{z}\:\:+\mathrm{2}{i}\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\right)\left({z}\:+{i}\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\right)−\mathrm{4}\left(−{z}^{\mathrm{2}} \:+\mathrm{2}{i}\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\:{z}\:+\mathrm{3}\right)}{\left({z}\:+{i}\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\right)^{\mathrm{5}} }\right. \\ $$$$\mathrm{2}{Res}\left(\varphi,{i}\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\right)=\left\{\:\frac{−\mathrm{4}\left(\frac{\mathrm{3}}{\mathrm{2}}\:−\mathrm{2}\:\frac{\mathrm{3}}{\mathrm{2}}\:+\mathrm{3}\right)}{\left(\mathrm{2}{i}\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\right)^{\mathrm{5}} }\right\} \\ $$$$=\:\frac{−\mathrm{6}}{\mathrm{2}^{\mathrm{5}} {i}\:\left(\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\right)\frac{\mathrm{9}}{\mathrm{4}}}\:=\:\:\frac{−\mathrm{6}}{\mathrm{8}{i}\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}.\mathrm{9}} \\ $$$$=\:\frac{−\mathrm{2}.\mathrm{3}}{\mathrm{2}.\mathrm{4}{i}.\mathrm{3}.\mathrm{3}\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}}\:=\:−\frac{\mathrm{1}}{\mathrm{4}{i}\frac{\sqrt{\mathrm{3}}}{\sqrt{\mathrm{2}}}}\:=\:\frac{−\sqrt{\mathrm{2}}}{\mathrm{4}{i}\sqrt{\mathrm{3}}} \\ $$$${Res}\left(\varphi,{i}\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\right)=\:\frac{−\sqrt{\mathrm{2}}}{\mathrm{8}{i}\sqrt{\mathrm{3}}} \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:\frac{−\sqrt{\mathrm{2}}}{\mathrm{8}{i}\sqrt{\mathrm{3}}}\:=\:\frac{−\pi\sqrt{\mathrm{2}}}{\mathrm{4}\sqrt{\mathrm{3}}}\:. \\ $$

Commented by abdo.msup.com last updated on 04/Jun/18

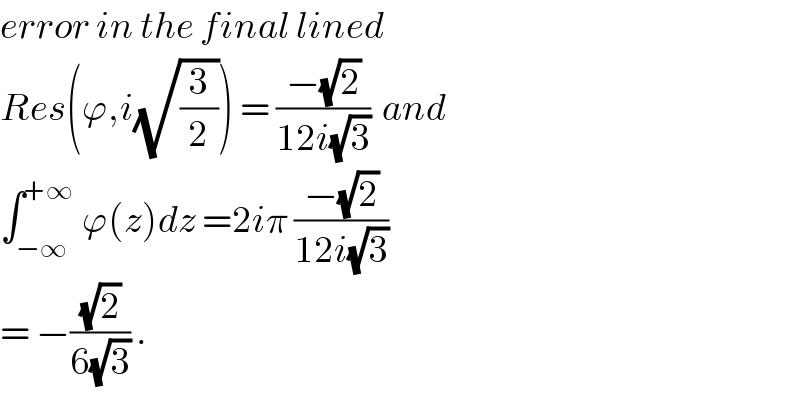
error in the final lined Res(ϕ,i(√(3/2))) = ((−(√2))/(12i(√3))) and ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ ((−(√2))/(12i(√3))) = −((√2)/(6(√3))) .

$${error}\:{in}\:{the}\:{final}\:{lined} \\ $$$${Res}\left(\varphi,{i}\sqrt{\frac{\mathrm{3}}{\mathrm{2}}}\right)\:=\:\frac{−\sqrt{\mathrm{2}}}{\mathrm{12}{i}\sqrt{\mathrm{3}}}\:\:{and} \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:\frac{−\sqrt{\mathrm{2}}}{\mathrm{12}{i}\sqrt{\mathrm{3}}}\: \\ $$$$=\:−\frac{\sqrt{\mathrm{2}}}{\mathrm{6}\sqrt{\mathrm{3}}}\:. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com