
Question Number 36425 by abdo.msup.com last updated on 01/Jun/18
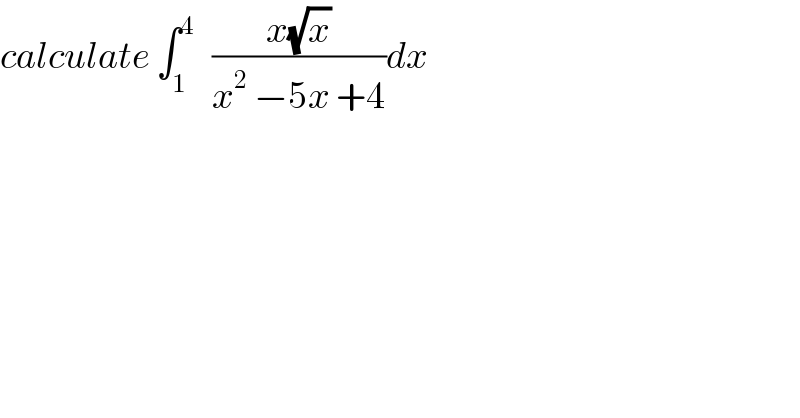
$${calculate}\:\int_{\mathrm{1}} ^{\mathrm{4}} \:\:\:\frac{{x}\sqrt{{x}}}{{x}^{\mathrm{2}} \:−\mathrm{5}{x}\:+\mathrm{4}}{dx} \\ $$
Commented by abdo mathsup 649 cc last updated on 03/Jun/18
![let put I = ∫_1 ^4 ((x(√x))/(x^2 −5x +4))dx changement (√x)=t give I = ∫_1 ^2 (t^3 /(t^4 −5t^2 +4))2t dt = 2 ∫_1 ^2 ((t^4 −5t^2 +4 +5t^2 −4)/(t^4 −5t^2 +4))dt =2 +2∫_1 ^2 ((5t^2 −4)/(t^4 −5t^2 +4))dt let decompose F(t)= ((5t^2 −4)/(t^4 −5t^2 +4)) =G(u)= ((5u−4)/(u^2 −5u +4))( u=t^2 ) u^2 −5u +4 = u^2 −u −4u +4 u(u−1) −4(u−1) =(u−1)(u−4)⇒ F(t)= ((5t^2 −4)/((t^2 −1)(t^2 −4))) = ((5t^2 −4)/((t−1)(t+1)(t−2)(t+2))) =(a/(t−1)) +(b/(t+1)) + (c/(t−2)) +(d/(t+2)) a = (1/(2(−1)3)) =((−1)/6) b = (1/((−2)(−3)1)) =(1/6) c = ((16)/(3.4)) =(4/3) d = ((16)/((−3)(−1)(−4))) =−(4/3) ⇒ F(t) = −(1/(6(t−1))) +(1/(6(t+1))) +(4/(3(t−2))) −(4/(3(t+2))) ⇒ ∫_1 ^2 F(t)dt = (1/6)[ln∣((t+1)/(t−1))∣]_1 ^2 +(4/3)[ln∣((t−2)/(t+2))∣]_1 ^2 =∞](Q36607.png)
$${let}\:{put}\:{I}\:=\:\int_{\mathrm{1}} ^{\mathrm{4}} \:\:\:\frac{{x}\sqrt{{x}}}{{x}^{\mathrm{2}} \:−\mathrm{5}{x}\:+\mathrm{4}}{dx}\:{changement}\:\sqrt{{x}}={t} \\ $$$${give}\:{I}\:=\:\int_{\mathrm{1}} ^{\mathrm{2}} \:\:\:\:\frac{{t}^{\mathrm{3}} }{{t}^{\mathrm{4}} \:−\mathrm{5}{t}^{\mathrm{2}} \:+\mathrm{4}}\mathrm{2}{t}\:{dt} \\ $$$$=\:\mathrm{2}\:\int_{\mathrm{1}} ^{\mathrm{2}} \:\:\:\:\frac{{t}^{\mathrm{4}} \:−\mathrm{5}{t}^{\mathrm{2}} \:+\mathrm{4}\:+\mathrm{5}{t}^{\mathrm{2}} \:−\mathrm{4}}{{t}^{\mathrm{4}} \:−\mathrm{5}{t}^{\mathrm{2}} \:+\mathrm{4}}{dt} \\ $$$$=\mathrm{2}\:\:+\mathrm{2}\int_{\mathrm{1}} ^{\mathrm{2}} \:\:\:\frac{\mathrm{5}{t}^{\mathrm{2}} \:−\mathrm{4}}{{t}^{\mathrm{4}} \:−\mathrm{5}{t}^{\mathrm{2}} \:+\mathrm{4}}{dt}\:\:{let}\:{decompose} \\ $$$${F}\left({t}\right)=\:\frac{\mathrm{5}{t}^{\mathrm{2}} \:−\mathrm{4}}{{t}^{\mathrm{4}} \:−\mathrm{5}{t}^{\mathrm{2}} \:+\mathrm{4}}\:={G}\left({u}\right)=\:\frac{\mathrm{5}{u}−\mathrm{4}}{{u}^{\mathrm{2}} \:−\mathrm{5}{u}\:+\mathrm{4}}\left(\:\:{u}={t}^{\mathrm{2}} \right) \\ $$$${u}^{\mathrm{2}} −\mathrm{5}{u}\:+\mathrm{4}\:=\:{u}^{\mathrm{2}} \:−{u}\:\:−\mathrm{4}{u}\:+\mathrm{4} \\ $$$${u}\left({u}−\mathrm{1}\right)\:−\mathrm{4}\left({u}−\mathrm{1}\right)\:=\left({u}−\mathrm{1}\right)\left({u}−\mathrm{4}\right)\Rightarrow \\ $$$${F}\left({t}\right)=\:\frac{\mathrm{5}{t}^{\mathrm{2}} \:−\mathrm{4}}{\left({t}^{\mathrm{2}} −\mathrm{1}\right)\left({t}^{\mathrm{2}} −\mathrm{4}\right)}\:=\:\frac{\mathrm{5}{t}^{\mathrm{2}} \:−\mathrm{4}}{\left({t}−\mathrm{1}\right)\left({t}+\mathrm{1}\right)\left({t}−\mathrm{2}\right)\left({t}+\mathrm{2}\right)} \\ $$$$=\frac{{a}}{{t}−\mathrm{1}}\:+\frac{{b}}{{t}+\mathrm{1}}\:\:+\:\frac{{c}}{{t}−\mathrm{2}}\:+\frac{{d}}{{t}+\mathrm{2}} \\ $$$${a}\:=\:\:\frac{\mathrm{1}}{\mathrm{2}\left(−\mathrm{1}\right)\mathrm{3}}\:=\frac{−\mathrm{1}}{\mathrm{6}} \\ $$$${b}\:=\:\:\frac{\mathrm{1}}{\left(−\mathrm{2}\right)\left(−\mathrm{3}\right)\mathrm{1}}\:=\frac{\mathrm{1}}{\mathrm{6}} \\ $$$${c}\:=\:\frac{\mathrm{16}}{\mathrm{3}.\mathrm{4}}\:=\frac{\mathrm{4}}{\mathrm{3}} \\ $$$${d}\:=\:\frac{\mathrm{16}}{\left(−\mathrm{3}\right)\left(−\mathrm{1}\right)\left(−\mathrm{4}\right)}\:=−\frac{\mathrm{4}}{\mathrm{3}}\:\Rightarrow \\ $$$${F}\left({t}\right)\:=\:−\frac{\mathrm{1}}{\mathrm{6}\left({t}−\mathrm{1}\right)}\:+\frac{\mathrm{1}}{\mathrm{6}\left({t}+\mathrm{1}\right)}\:+\frac{\mathrm{4}}{\mathrm{3}\left({t}−\mathrm{2}\right)}\:−\frac{\mathrm{4}}{\mathrm{3}\left({t}+\mathrm{2}\right)}\:\Rightarrow \\ $$$$\int_{\mathrm{1}} ^{\mathrm{2}} \:{F}\left({t}\right){dt}\:=\:\frac{\mathrm{1}}{\mathrm{6}}\left[{ln}\mid\frac{{t}+\mathrm{1}}{{t}−\mathrm{1}}\mid\right]_{\mathrm{1}} ^{\mathrm{2}} \:\:+\frac{\mathrm{4}}{\mathrm{3}}\left[{ln}\mid\frac{{t}−\mathrm{2}}{{t}+\mathrm{2}}\mid\right]_{\mathrm{1}} ^{\mathrm{2}} \:=\infty \\ $$$$ \\ $$
Commented by abdo mathsup 649 cc last updated on 03/Jun/18
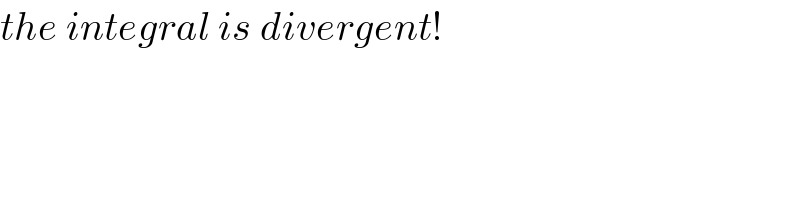
$${the}\:{integral}\:{is}\:{divergent}! \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 03/Jun/18
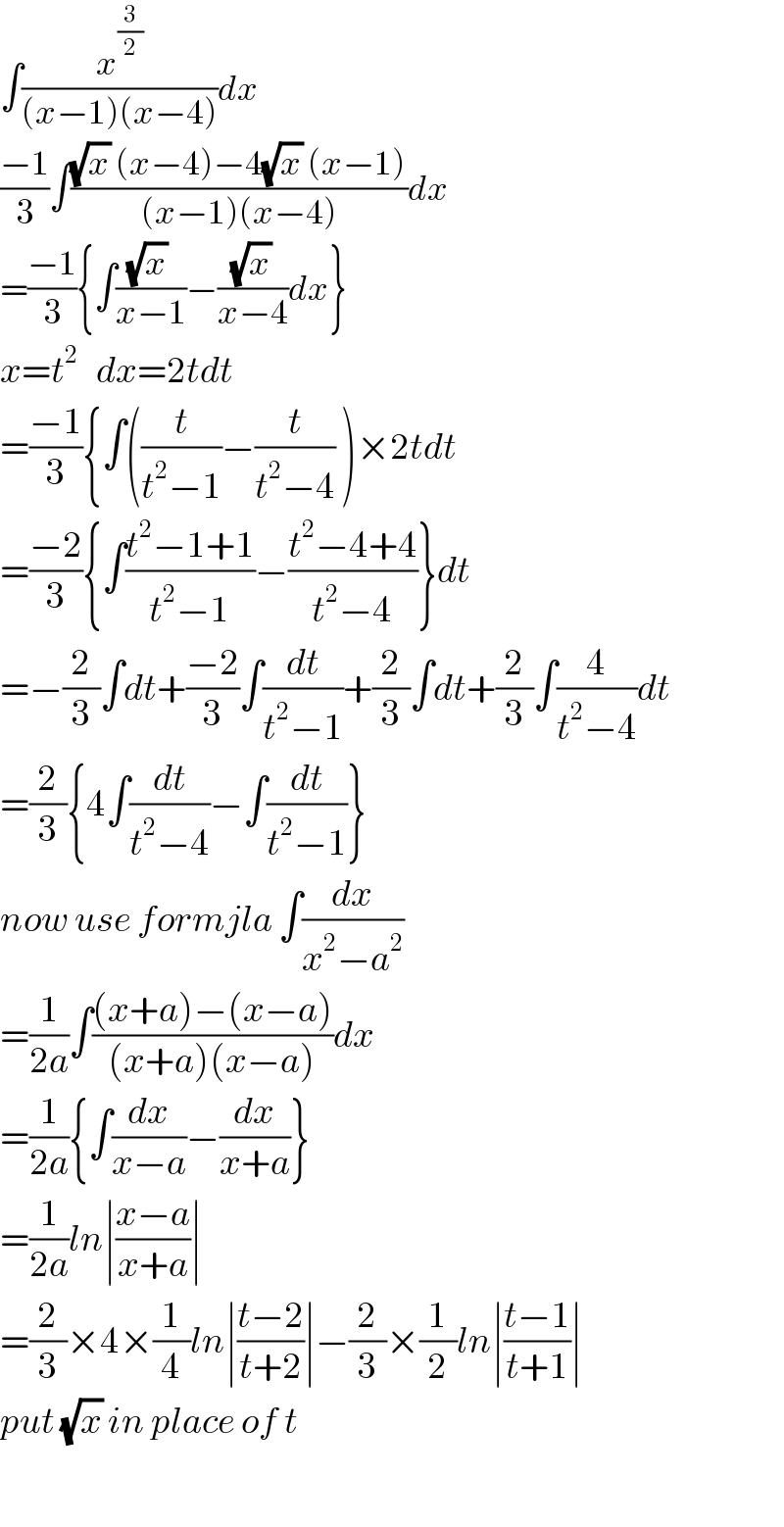
$$\int\frac{{x}^{\frac{\mathrm{3}}{\mathrm{2}}} }{\left({x}−\mathrm{1}\right)\left({x}−\mathrm{4}\right)}{dx} \\ $$$$\frac{−\mathrm{1}}{\mathrm{3}}\int\frac{\sqrt{{x}}\:\left({x}−\mathrm{4}\right)−\mathrm{4}\sqrt{{x}}\:\left({x}−\mathrm{1}\right)}{\left({x}−\mathrm{1}\right)\left({x}−\mathrm{4}\right)}{dx} \\ $$$$=\frac{−\mathrm{1}}{\mathrm{3}}\left\{\int\frac{\sqrt{{x}}\:}{{x}−\mathrm{1}}−\frac{\sqrt{{x}}}{{x}−\mathrm{4}}{dx}\right\} \\ $$$${x}={t}^{\mathrm{2}} \:\:\:{dx}=\mathrm{2}{tdt} \\ $$$$=\frac{−\mathrm{1}}{\mathrm{3}}\left\{\int\left(\frac{{t}}{{t}^{\mathrm{2}} −\mathrm{1}}−\frac{{t}}{{t}^{\mathrm{2}} −\mathrm{4}}\:\right)×\mathrm{2}{tdt}\right. \\ $$$$=\frac{−\mathrm{2}}{\mathrm{3}}\left\{\int\frac{{t}^{\mathrm{2}} −\mathrm{1}+\mathrm{1}}{{t}^{\mathrm{2}} −\mathrm{1}}−\frac{{t}^{\mathrm{2}} −\mathrm{4}+\mathrm{4}}{{t}^{\mathrm{2}} −\mathrm{4}}\right\}{dt} \\ $$$$=−\frac{\mathrm{2}}{\mathrm{3}}\int{dt}+\frac{−\mathrm{2}}{\mathrm{3}}\int\frac{{dt}}{{t}^{\mathrm{2}} −\mathrm{1}}+\frac{\mathrm{2}}{\mathrm{3}}\int{dt}+\frac{\mathrm{2}}{\mathrm{3}}\int\frac{\mathrm{4}}{{t}^{\mathrm{2}} −\mathrm{4}}{dt} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\left\{\mathrm{4}\int\frac{{dt}}{{t}^{\mathrm{2}} −\mathrm{4}}−\int\frac{{dt}}{{t}^{\mathrm{2}} −\mathrm{1}}\right\} \\ $$$${now}\:{use}\:{formjla}\:\int\frac{{dx}}{{x}^{\mathrm{2}} −{a}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{a}}\int\frac{\left({x}+{a}\right)−\left({x}−{a}\right)}{\left({x}+{a}\right)\left({x}−{a}\right)}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{a}}\left\{\int\frac{{dx}}{{x}−{a}}−\frac{{dx}}{{x}+{a}}\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}{a}}{ln}\mid\frac{{x}−{a}}{{x}+{a}}\mid \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}×\mathrm{4}×\frac{\mathrm{1}}{\mathrm{4}}{ln}\mid\frac{{t}−\mathrm{2}}{{t}+\mathrm{2}}\mid−\frac{\mathrm{2}}{\mathrm{3}}×\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid\frac{{t}−\mathrm{1}}{{t}+\mathrm{1}}\mid \\ $$$${put}\:\sqrt{{x}}\:{in}\:{place}\:{of}\:{t} \\ $$$$ \\ $$
Commented by ajfour last updated on 03/Jun/18
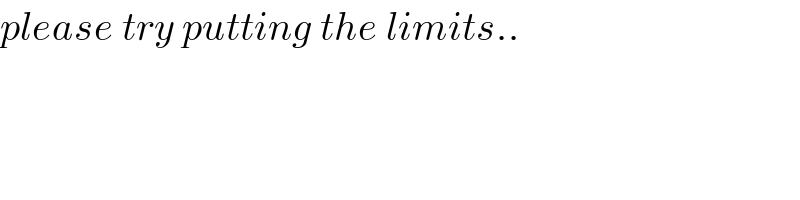
$${please}\:{try}\:{putting}\:{the}\:{limits}.. \\ $$
Answered by ajfour last updated on 03/Jun/18
![let x=t^2 ⇒ dx=2tdt I=∫_1 ^( 2) ((2t^4 dt)/((t^2 −1)(t^2 −4))) =2∫_1 ^( 2) dt + 2∫_1 ^( 2) ((5t^2 −4)/((t^2 −1)(t^2 −4))) dt =30−(2/3)∫_1 ^( 2) (dt/(t^2 −1))+((32)/3)∫_1 ^( 2) (dt/(t^2 −4)) =30−lim_(h→0) [(1/3)ln ((1/3)×(2/h)) +(8/3)ln (((−h)/4)×(3/(−1)))] =30+(1/3)lim_(h→0) (ln(((3h)/4))^8 (((3h)/2))) = −∞ (divergent).](Q36600.png)
$${let}\:{x}={t}^{\mathrm{2}} \:\:\:\Rightarrow\:\:{dx}=\mathrm{2}{tdt} \\ $$$${I}=\int_{\mathrm{1}} ^{\:\:\mathrm{2}} \frac{\mathrm{2}{t}^{\mathrm{4}} {dt}}{\left({t}^{\mathrm{2}} −\mathrm{1}\right)\left({t}^{\mathrm{2}} −\mathrm{4}\right)} \\ $$$$\:\:=\mathrm{2}\int_{\mathrm{1}} ^{\:\:\mathrm{2}} {dt}\:+\:\mathrm{2}\int_{\mathrm{1}} ^{\:\:\mathrm{2}} \frac{\mathrm{5}{t}^{\mathrm{2}} −\mathrm{4}}{\left({t}^{\mathrm{2}} −\mathrm{1}\right)\left({t}^{\mathrm{2}} −\mathrm{4}\right)}\:{dt} \\ $$$$\:\:=\mathrm{30}−\frac{\mathrm{2}}{\mathrm{3}}\int_{\mathrm{1}} ^{\:\:\mathrm{2}} \frac{{dt}}{{t}^{\mathrm{2}} −\mathrm{1}}+\frac{\mathrm{32}}{\mathrm{3}}\int_{\mathrm{1}} ^{\:\:\mathrm{2}} \frac{{dt}}{{t}^{\mathrm{2}} −\mathrm{4}} \\ $$$$\:\:=\mathrm{30}−\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\:\left(\frac{\mathrm{1}}{\mathrm{3}}×\frac{\mathrm{2}}{{h}}\right)\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:+\frac{\mathrm{8}}{\mathrm{3}}\mathrm{ln}\:\left(\frac{−{h}}{\mathrm{4}}×\frac{\mathrm{3}}{−\mathrm{1}}\right)\right]\: \\ $$$$\:\:=\mathrm{30}+\frac{\mathrm{1}}{\mathrm{3}}\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{ln}\left(\frac{\mathrm{3}{h}}{\mathrm{4}}\right)^{\mathrm{8}} \left(\frac{\mathrm{3}{h}}{\mathrm{2}}\right)\right)\: \\ $$$$\:=\:−\infty\:\:\:\left({divergent}\right). \\ $$
