Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 36435 by prof Abdo imad last updated on 02/Jun/18

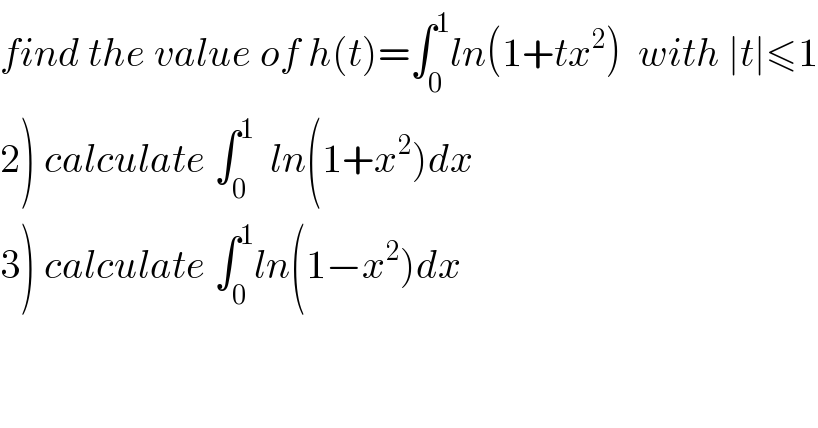
find the value of h(t)=∫_0 ^1 ln(1+tx^2 ) with ∣t∣≤1 2) calculate ∫_0 ^1 ln(1+x^2 )dx 3) calculate ∫_0 ^1 ln(1−x^2 )dx

$${find}\:{the}\:{value}\:{of}\:{h}\left({t}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{tx}^{\mathrm{2}} \right)\:\:{with}\:\mid{t}\mid\leqslant\mathrm{1} \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right){dx} \\ $$$$\left.\mathrm{3}\right)\:{calculate}\:\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}−{x}^{\mathrm{2}} \right){dx} \\ $$

Commented by abdo.msup.com last updated on 03/Jun/18

another method but easy ∫_0 ^1 ln(1−x^2 )dx = ∫_0 ^1 ln(1−x)dx + ∫_0 ^1 ln(1+x)dx but ∫_0 ^1 ln(1−x)dx =_(1−x=t) −∫_1 ^0 lnt dt = ∫_0 ^1 ln(t)dt = [tln(t)]_0 ^1 =0 ∫_0 ^1 ln(1+x)dx =_(1+x=t) ∫_1 ^2 ln(t)dt =[ tln(t)]_1 ^2 =2ln(2) so ∫_0 ^1 ln(1−x^2 )dx =2ln(2) .

$${another}\:{method}\:{but}\:{easy} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:{ln}\left(\mathrm{1}−{x}^{\mathrm{2}} \right){dx}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{ln}\left(\mathrm{1}−{x}\right){dx}\:+ \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:{ln}\left(\mathrm{1}+{x}\right){dx}\:{but} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:{ln}\left(\mathrm{1}−{x}\right){dx}\:=_{\mathrm{1}−{x}={t}} \:−\int_{\mathrm{1}} ^{\mathrm{0}} \:{lnt}\:{dt} \\ $$$$=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{ln}\left({t}\right){dt}\:=\:\left[{tln}\left({t}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:=\mathrm{0} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{x}\right){dx}\:=_{\mathrm{1}+{x}={t}} \:\int_{\mathrm{1}} ^{\mathrm{2}} \:{ln}\left({t}\right){dt} \\ $$$$=\left[\:{tln}\left({t}\right)\right]_{\mathrm{1}} ^{\mathrm{2}} \:\:=\mathrm{2}{ln}\left(\mathrm{2}\right)\:{so} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:{ln}\left(\mathrm{1}−{x}^{\mathrm{2}} \right){dx}\:=\mathrm{2}{ln}\left(\mathrm{2}\right)\:. \\ $$

Commented by abdo.msup.com last updated on 03/Jun/18

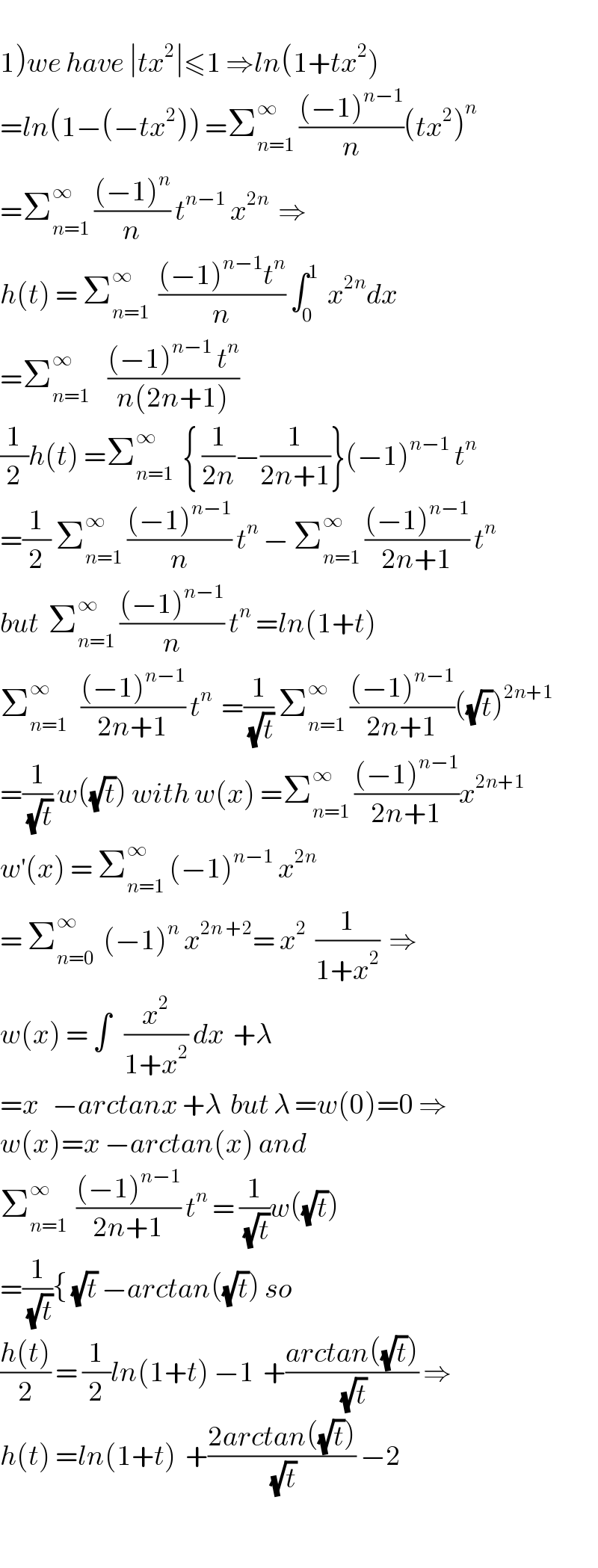
1)we have ∣tx^2 ∣≤1 ⇒ln(1+tx^2 ) =ln(1−(−tx^2 )) =Σ_(n=1) ^∞ (((−1)^(n−1) )/n)(tx^2 )^n =Σ_(n=1) ^∞ (((−1)^n )/n) t^(n−1) x^(2n) ⇒ h(t) = Σ_(n=1) ^∞ (((−1)^(n−1) t^n )/n) ∫_0 ^1 x^(2n) dx =Σ_(n=1) ^∞ (((−1)^(n−1) t^n )/(n(2n+1))) (1/2)h(t) =Σ_(n=1) ^∞ { (1/(2n))−(1/(2n+1))}(−1)^(n−1) t^n =(1/2) Σ_(n=1) ^∞ (((−1)^(n−1) )/n) t^n − Σ_(n=1) ^∞ (((−1)^(n−1) )/(2n+1)) t^n but Σ_(n=1) ^∞ (((−1)^(n−1) )/n) t^n =ln(1+t) Σ_(n=1) ^∞ (((−1)^(n−1) )/(2n+1)) t^n =(1/(√t)) Σ_(n=1) ^∞ (((−1)^(n−1) )/(2n+1))((√t))^(2n+1) =(1/(√t)) w((√t)) with w(x) =Σ_(n=1) ^∞ (((−1)^(n−1) )/(2n+1))x^(2n+1) w^′ (x) = Σ_(n=1) ^∞ (−1)^(n−1) x^(2n) = Σ_(n=0) ^∞ (−1)^n x^(2n +2) = x^2 (1/(1+x^2 )) ⇒ w(x) = ∫ (x^2 /(1+x^2 )) dx +λ =x −arctanx +λ but λ =w(0)=0 ⇒ w(x)=x −arctan(x) and Σ_(n=1) ^∞ (((−1)^(n−1) )/(2n+1)) t^n = (1/(√t))w((√t)) =(1/(√t)){ (√t) −arctan((√t)) so ((h(t))/2) = (1/2)ln(1+t) −1 +((arctan((√t)))/(√t)) ⇒ h(t) =ln(1+t) +((2arctan((√t)))/(√t)) −2

$$ \\ $$$$\left.\mathrm{1}\right){we}\:{have}\:\mid{tx}^{\mathrm{2}} \mid\leqslant\mathrm{1}\:\Rightarrow{ln}\left(\mathrm{1}+{tx}^{\mathrm{2}} \right) \\ $$$$={ln}\left(\mathrm{1}−\left(−{tx}^{\mathrm{2}} \right)\right)\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\left({tx}^{\mathrm{2}} \right)^{{n}} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}}\:{t}^{{n}−\mathrm{1}} \:{x}^{\mathrm{2}{n}} \:\:\Rightarrow \\ $$$${h}\left({t}\right)\:=\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} {t}^{{n}} }{{n}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:{x}^{\mathrm{2}{n}} {dx} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \:{t}^{{n}} }{{n}\left(\mathrm{2}{n}+\mathrm{1}\right)} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{h}\left({t}\right)\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\left\{\:\frac{\mathrm{1}}{\mathrm{2}{n}}−\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\right\}\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \:{t}^{{n}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\:{t}^{{n}} \:−\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{\mathrm{2}{n}+\mathrm{1}}\:{t}^{{n}} \\ $$$${but}\:\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\:{t}^{{n}} \:={ln}\left(\mathrm{1}+{t}\right) \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{\mathrm{2}{n}+\mathrm{1}}\:{t}^{{n}} \:\:=\frac{\mathrm{1}}{\sqrt{{t}}}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{\mathrm{2}{n}+\mathrm{1}}\left(\sqrt{{t}}\right)^{\mathrm{2}{n}+\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\sqrt{{t}}}\:{w}\left(\sqrt{{t}}\right)\:{with}\:{w}\left({x}\right)\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{\mathrm{2}{n}+\mathrm{1}}{x}^{\mathrm{2}{n}+\mathrm{1}} \\ $$$${w}^{'} \left({x}\right)\:=\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \:{x}^{\mathrm{2}{n}} \\ $$$$=\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\left(−\mathrm{1}\right)^{{n}} \:{x}^{\mathrm{2}{n}\:+\mathrm{2}} =\:{x}^{\mathrm{2}} \:\:\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }\:\:\Rightarrow \\ $$$${w}\left({x}\right)\:=\:\int\:\:\:\frac{{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx}\:\:+\lambda \\ $$$$={x}\:\:\:−{arctanx}\:+\lambda\:\:{but}\:\lambda\:={w}\left(\mathrm{0}\right)=\mathrm{0}\:\Rightarrow \\ $$$${w}\left({x}\right)={x}\:−{arctan}\left({x}\right)\:{and} \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{\mathrm{2}{n}+\mathrm{1}}\:{t}^{{n}} \:=\:\frac{\mathrm{1}}{\sqrt{{t}}}{w}\left(\sqrt{{t}}\right) \\ $$$$=\frac{\mathrm{1}}{\sqrt{{t}}}\left\{\:\sqrt{{t}}\:−{arctan}\left(\sqrt{{t}}\right)\:{so}\right. \\ $$$$\frac{{h}\left({t}\right)}{\mathrm{2}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+{t}\right)\:−\mathrm{1}\:\:+\frac{{arctan}\left(\sqrt{{t}}\right)}{\sqrt{{t}}}\:\Rightarrow \\ $$$${h}\left({t}\right)\:={ln}\left(\mathrm{1}+{t}\right)\:\:+\frac{\mathrm{2}{arctan}\left(\sqrt{{t}}\right)}{\sqrt{{t}}}\:−\mathrm{2} \\ $$$$ \\ $$

Commented by abdo.msup.com last updated on 03/Jun/18

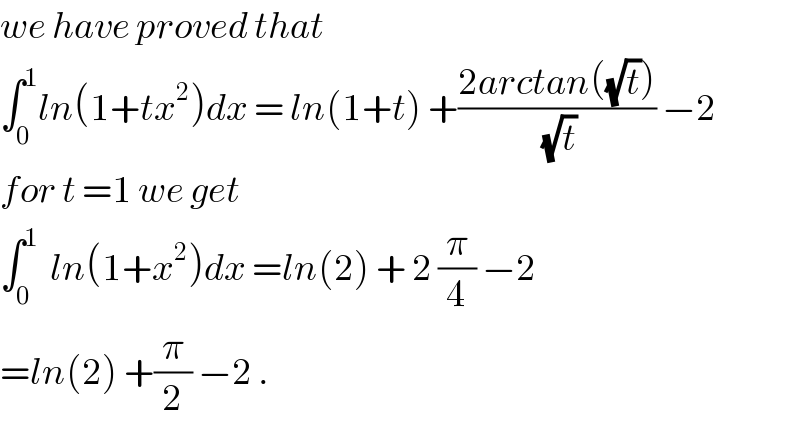
we have proved that ∫_0 ^1 ln(1+tx^2 )dx = ln(1+t) +((2arctan((√t)))/(√t)) −2 for t =1 we get ∫_0 ^1 ln(1+x^2 )dx =ln(2) + 2 (π/4) −2 =ln(2) +(π/2) −2 .

$${we}\:{have}\:{proved}\:{that}\: \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{tx}^{\mathrm{2}} \right){dx}\:=\:{ln}\left(\mathrm{1}+{t}\right)\:+\frac{\mathrm{2}{arctan}\left(\sqrt{{t}}\right)}{\sqrt{{t}}}\:−\mathrm{2} \\ $$$${for}\:{t}\:=\mathrm{1}\:{we}\:{get} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\:{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right){dx}\:={ln}\left(\mathrm{2}\right)\:+\:\mathrm{2}\:\frac{\pi}{\mathrm{4}}\:−\mathrm{2} \\ $$$$={ln}\left(\mathrm{2}\right)\:+\frac{\pi}{\mathrm{2}}\:−\mathrm{2}\:. \\ $$

Commented by abdo.msup.com last updated on 03/Jun/18

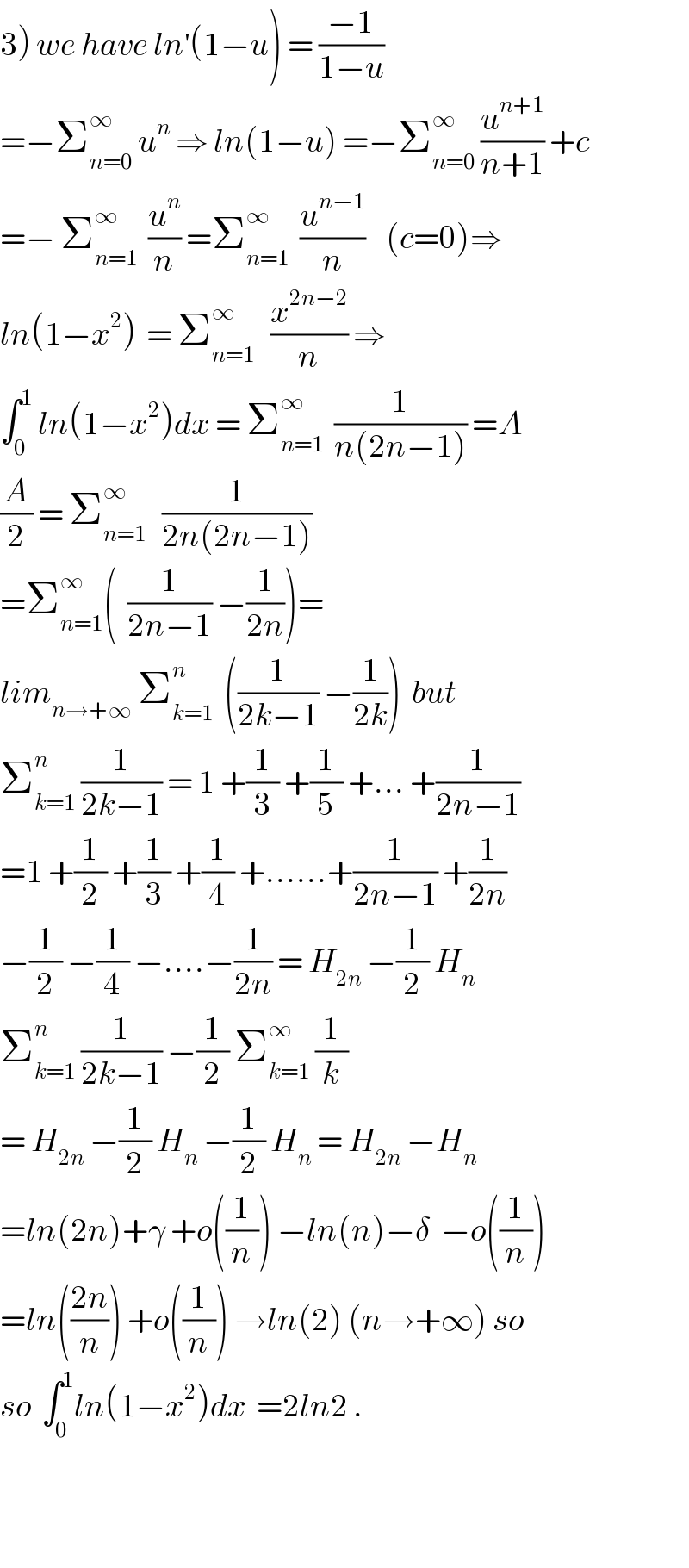
3) we have ln^′ (1−u) = ((−1)/(1−u)) =−Σ_(n=0) ^∞ u^n ⇒ ln(1−u) =−Σ_(n=0) ^∞ (u^(n+1) /(n+1)) +c =− Σ_(n=1) ^∞ (u^n /n) =Σ_(n=1) ^∞ (u^(n−1) /n) (c=0)⇒ ln(1−x^2 ) = Σ_(n=1) ^∞ (x^(2n−2) /n) ⇒ ∫_0 ^1 ln(1−x^2 )dx = Σ_(n=1) ^∞ (1/(n(2n−1))) =A (A/2) = Σ_(n=1) ^∞ (1/(2n(2n−1))) =Σ_(n=1) ^∞ ( (1/(2n−1)) −(1/(2n)))= lim_(n→+∞) Σ_(k=1) ^n ((1/(2k−1)) −(1/(2k))) but Σ_(k=1) ^n (1/(2k−1)) = 1 +(1/3) +(1/5) +... +(1/(2n−1)) =1 +(1/2) +(1/3) +(1/4) +......+(1/(2n−1)) +(1/(2n)) −(1/2) −(1/4) −....−(1/(2n)) = H_(2n) −(1/2) H_n Σ_(k=1) ^n (1/(2k−1)) −(1/2) Σ_(k=1) ^∞ (1/k) = H_(2n) −(1/2) H_n −(1/2) H_n = H_(2n) −H_n =ln(2n)+γ +o((1/n)) −ln(n)−δ −o((1/n)) =ln(((2n)/n)) +o((1/n)) →ln(2) (n→+∞) so so ∫_0 ^1 ln(1−x^2 )dx =2ln2 .

$$\left.\mathrm{3}\right)\:{we}\:{have}\:{ln}^{'} \left(\mathrm{1}−{u}\right)\:=\:\frac{−\mathrm{1}}{\mathrm{1}−{u}} \\ $$$$=−\sum_{{n}=\mathrm{0}} ^{\infty} \:{u}^{{n}} \:\Rightarrow\:{ln}\left(\mathrm{1}−{u}\right)\:=−\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{u}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}\:+{c} \\ $$$$=−\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{{u}^{{n}} }{{n}}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{{u}^{{n}−\mathrm{1}} }{{n}}\:\:\:\:\left({c}=\mathrm{0}\right)\Rightarrow \\ $$$${ln}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\:\:=\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\frac{{x}^{\mathrm{2}{n}−\mathrm{2}} }{{n}}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:{ln}\left(\mathrm{1}−{x}^{\mathrm{2}} \right){dx}\:=\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{1}}{{n}\left(\mathrm{2}{n}−\mathrm{1}\right)}\:={A} \\ $$$$\frac{{A}}{\mathrm{2}}\:=\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\frac{\mathrm{1}}{\mathrm{2}{n}\left(\mathrm{2}{n}−\mathrm{1}\right)} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \left(\:\:\frac{\mathrm{1}}{\mathrm{2}{n}−\mathrm{1}}\:−\frac{\mathrm{1}}{\mathrm{2}{n}}\right)= \\ $$$${lim}_{{n}\rightarrow+\infty} \:\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\left(\frac{\mathrm{1}}{\mathrm{2}{k}−\mathrm{1}}\:−\frac{\mathrm{1}}{\mathrm{2}{k}}\right)\:\:{but} \\ $$$$\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{\mathrm{2}{k}−\mathrm{1}}\:=\:\mathrm{1}\:+\frac{\mathrm{1}}{\mathrm{3}}\:+\frac{\mathrm{1}}{\mathrm{5}}\:+...\:+\frac{\mathrm{1}}{\mathrm{2}{n}−\mathrm{1}} \\ $$$$=\mathrm{1}\:+\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{3}}\:+\frac{\mathrm{1}}{\mathrm{4}}\:+......+\frac{\mathrm{1}}{\mathrm{2}{n}−\mathrm{1}}\:+\frac{\mathrm{1}}{\mathrm{2}{n}} \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{4}}\:−....−\frac{\mathrm{1}}{\mathrm{2}{n}}\:=\:{H}_{\mathrm{2}{n}} \:−\frac{\mathrm{1}}{\mathrm{2}}\:{H}_{{n}} \\ $$$$\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{\mathrm{2}{k}−\mathrm{1}}\:−\frac{\mathrm{1}}{\mathrm{2}}\:\sum_{{k}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{{k}} \\ $$$$=\:{H}_{\mathrm{2}{n}} \:−\frac{\mathrm{1}}{\mathrm{2}}\:{H}_{{n}} \:−\frac{\mathrm{1}}{\mathrm{2}}\:{H}_{{n}} \:=\:{H}_{\mathrm{2}{n}} \:−{H}_{{n}} \\ $$$$={ln}\left(\mathrm{2}{n}\right)+\gamma\:+{o}\left(\frac{\mathrm{1}}{{n}}\right)\:−{ln}\left({n}\right)−\delta\:\:−{o}\left(\frac{\mathrm{1}}{{n}}\right) \\ $$$$={ln}\left(\frac{\mathrm{2}{n}}{{n}}\right)\:+{o}\left(\frac{\mathrm{1}}{{n}}\right)\:\rightarrow{ln}\left(\mathrm{2}\right)\:\left({n}\rightarrow+\infty\right)\:{so} \\ $$$${so}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}−{x}^{\mathrm{2}} \right){dx}\:\:=\mathrm{2}{ln}\mathrm{2}\:. \\ $$$$ \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com