
Question and Answers Forum
Question Number 36436 by prof Abdo imad last updated on 02/Jun/18
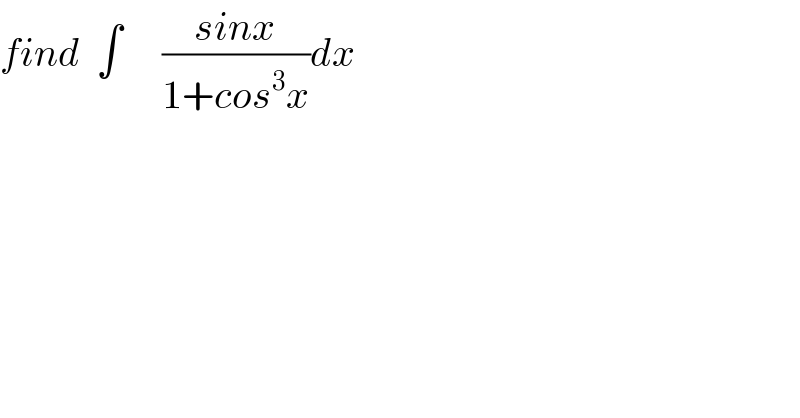
Answered by tanmay.chaudhury50@gmail.com last updated on 02/Jun/18
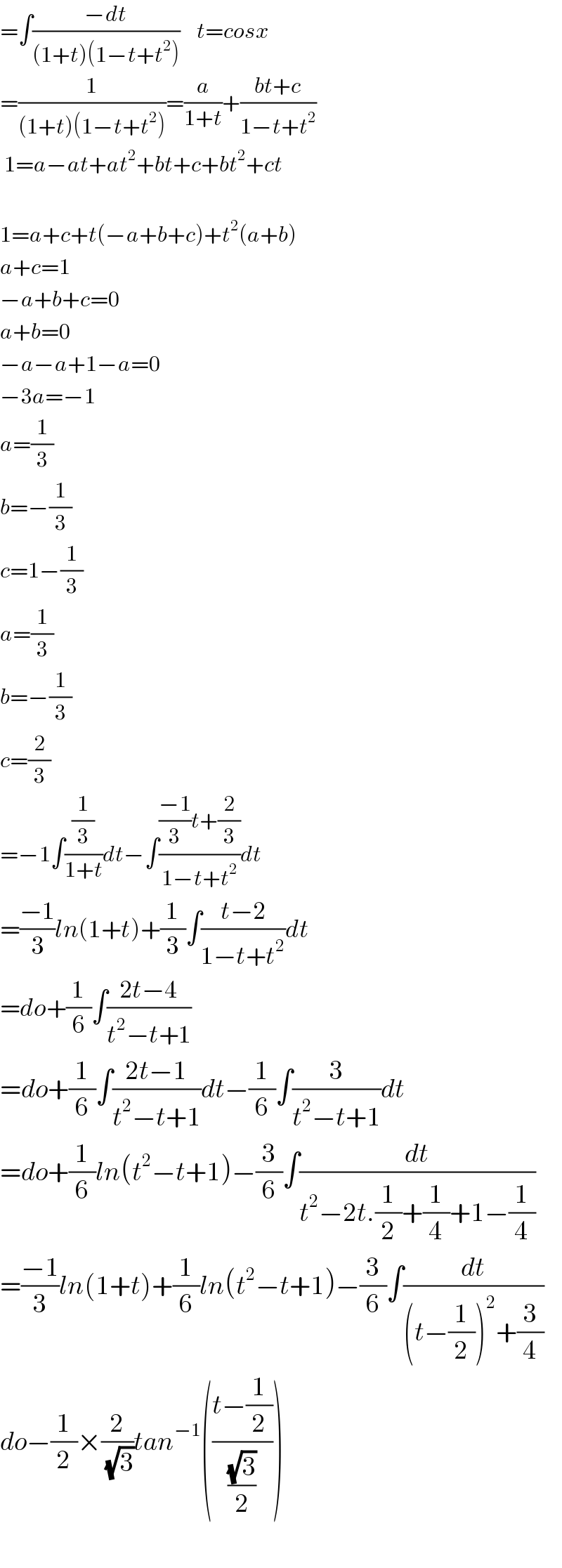
Answered by MJS last updated on 02/Jun/18
![∫((sin x)/(1+cos^3 x))dx= [((t=2arctan x → dx=((2dt)/(1+t^2 )))),((sin x=((2t)/(1+t^2 )) cos x=((1−t^2 )/(1+t^2 )))) ] =2∫((t^3 +t)/(3t^4 +1))dt= [u=t^2 → dt=(du/(2t))] =∫((u+1)/(3u^2 +1))du=∫(u/(3u^2 +1))du+∫(du/(3u^2 +1))= [v=3u^2 +1 → du=(6/dv); w=(√3)u → du=((√3)/3)dw] =(1/6)∫(dv/v)+((√3)/3)∫(dw/(w^2 +1))= =(1/6)ln v+((√3)/3)arctan w= =(1/6)ln(3u^2 +1)+((√3)/3)arctan((√3)u)= =(1/6)ln(3t^4 +1)+((√3)/3)arctan((√3)t^2 )= =(1/6)ln(48(1+arctan^4 x))+((√3)/3)arctan(4(√3)arctan^2 x)+C](Q36495.png)
| ||
Question and Answers Forum | ||
Question Number 36436 by prof Abdo imad last updated on 02/Jun/18 | ||
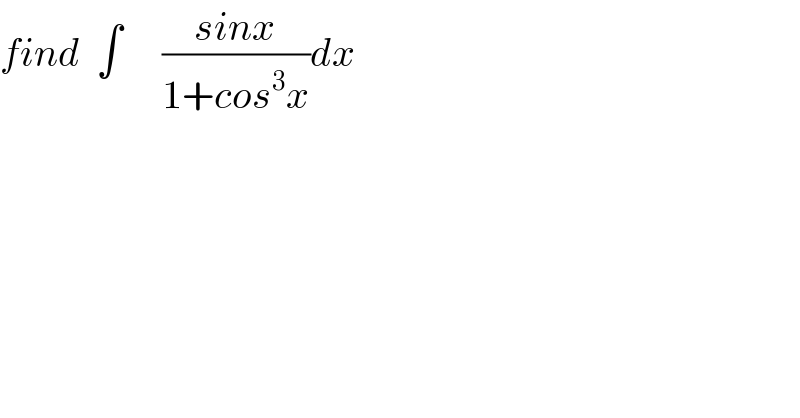 | ||
Answered by tanmay.chaudhury50@gmail.com last updated on 02/Jun/18 | ||
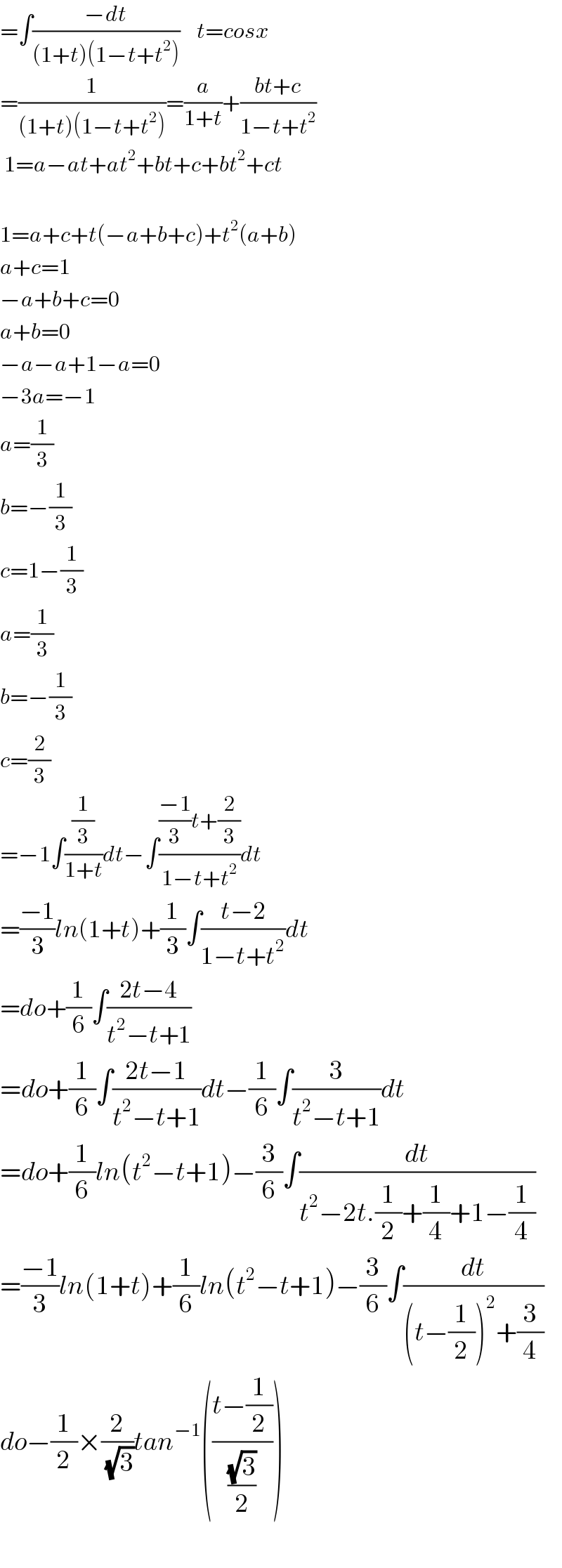 | ||
| ||
Answered by MJS last updated on 02/Jun/18 | ||
![∫((sin x)/(1+cos^3 x))dx= [((t=2arctan x → dx=((2dt)/(1+t^2 )))),((sin x=((2t)/(1+t^2 )) cos x=((1−t^2 )/(1+t^2 )))) ] =2∫((t^3 +t)/(3t^4 +1))dt= [u=t^2 → dt=(du/(2t))] =∫((u+1)/(3u^2 +1))du=∫(u/(3u^2 +1))du+∫(du/(3u^2 +1))= [v=3u^2 +1 → du=(6/dv); w=(√3)u → du=((√3)/3)dw] =(1/6)∫(dv/v)+((√3)/3)∫(dw/(w^2 +1))= =(1/6)ln v+((√3)/3)arctan w= =(1/6)ln(3u^2 +1)+((√3)/3)arctan((√3)u)= =(1/6)ln(3t^4 +1)+((√3)/3)arctan((√3)t^2 )= =(1/6)ln(48(1+arctan^4 x))+((√3)/3)arctan(4(√3)arctan^2 x)+C](Q36495.png) | ||
| ||