
Question and Answers Forum
Question Number 36439 by prof Abdo imad last updated on 02/Jun/18
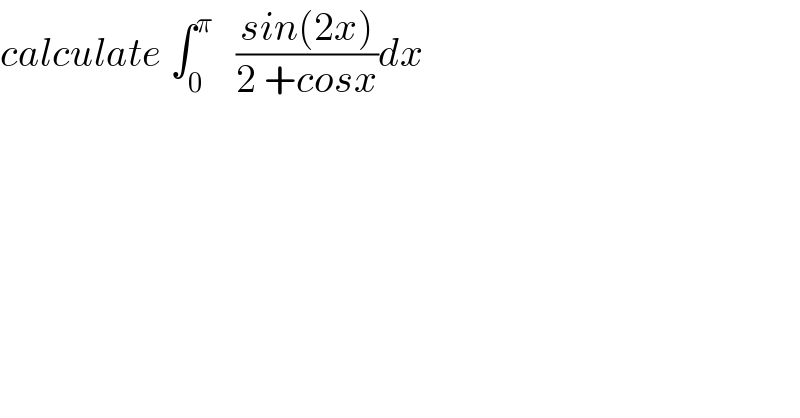
Commented by abdo.msup.com last updated on 03/Jun/18
![I = ∫_0 ^π ((2sinx cosx)/(2+cosx)) dx changement cosx =t give −sinx dx =dt I = ∫_1 ^(−1) ((−2t dt)/(2+t)) =2 ∫_(−1) ^1 (t/(t+2))dt =2 ∫_(−1) ^1 ((t+2 −2)/(t+2))dt =4 −4 [ln∣t+2∣]_(−1) ^1 =4 −4( ln(3)) I =4 −4ln(3) .](Q36637.png)
Answered by ajfour last updated on 02/Jun/18

Commented by MJS last updated on 02/Jun/18

| ||
Question and Answers Forum | ||
Question Number 36439 by prof Abdo imad last updated on 02/Jun/18 | ||
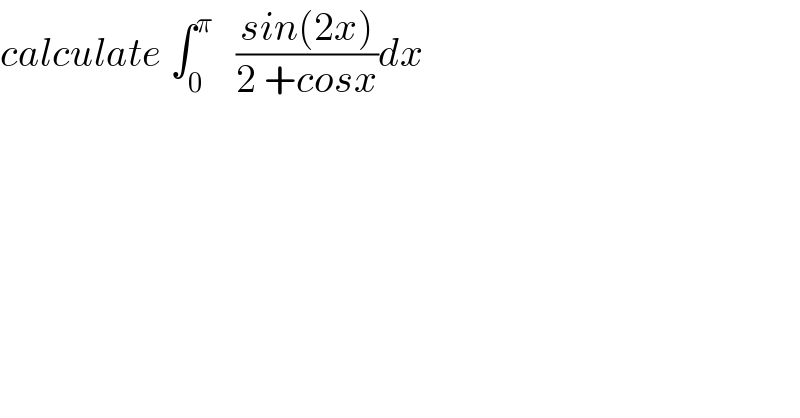 | ||
Commented by abdo.msup.com last updated on 03/Jun/18 | ||
![I = ∫_0 ^π ((2sinx cosx)/(2+cosx)) dx changement cosx =t give −sinx dx =dt I = ∫_1 ^(−1) ((−2t dt)/(2+t)) =2 ∫_(−1) ^1 (t/(t+2))dt =2 ∫_(−1) ^1 ((t+2 −2)/(t+2))dt =4 −4 [ln∣t+2∣]_(−1) ^1 =4 −4( ln(3)) I =4 −4ln(3) .](Q36637.png) | ||
Answered by ajfour last updated on 02/Jun/18 | ||
 | ||
| ||
Commented by MJS last updated on 02/Jun/18 | ||
 | ||