Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 3644 by prakash jain last updated on 17/Dec/15

An hexagon of unit side is drawn on plane. Draw a square having the same area as the hexagon using only unmarked ruler and compass. What if an n−gon with unit edges is given? Is it always possible to draw a square of the same area as n−gon using ruler and compass.

$$\mathrm{An}\:\mathrm{hexagon}\:\mathrm{of}\:\mathrm{unit}\:\mathrm{side}\:\mathrm{is}\:\mathrm{drawn}\:\mathrm{on}\:\mathrm{plane}. \\ $$$$\mathrm{Draw}\:\mathrm{a}\:\mathrm{square}\:\mathrm{having}\:\mathrm{the}\:\mathrm{same}\:\mathrm{area}\:\mathrm{as}\:\mathrm{the} \\ $$$$\mathrm{hexagon}\:\mathrm{using}\:\mathrm{only}\:\mathrm{unmarked}\:\mathrm{ruler}\:\mathrm{and}\: \\ $$$$\mathrm{compass}. \\ $$$$\mathrm{What}\:\mathrm{if}\:\mathrm{an}\:{n}−\mathrm{gon}\:\mathrm{with}\:\mathrm{unit}\:\mathrm{edges}\:\mathrm{is}\:\mathrm{given}? \\ $$$$\mathrm{Is}\:\mathrm{it}\:\mathrm{always}\:\mathrm{possible}\:\mathrm{to}\:\mathrm{draw}\:\mathrm{a}\:\mathrm{square} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{same}\:\mathrm{area}\:\mathrm{as}\:{n}−\mathrm{gon}\:\mathrm{using}\:\mathrm{ruler} \\ $$$$\mathrm{and}\:\mathrm{compass}. \\ $$

Commented by Rasheed Soomro last updated on 17/Dec/15

A hexagon of unit side consists of 6 triangles of unit side. Area of triangle of unit side(▲) : ▲=(√((3/2)((3/2)−1)^3 ))=(√((3/2)×(1/2^3 ))) =((√3)/4) Area of hexagon of unit side (A): A=6▲=6×((√3)/4)=((3(√3))/2)=(√((27)/4)) Square of area ((3(√3))/2) has its side(s) equal to (√(√((27)/4))) So ultimately we need to draw a line segment of measure (√(√((27)/4))) units One way may be as under: •Extend the side of hexagon 27 times. Say it AB • Cut off AC=(1/4)AB . •Cut off CD equal to hexagon side from AB. Continue

$$\mathrm{A}\:\mathrm{hexagon}\:\mathrm{of}\:\mathrm{unit}\:\mathrm{side}\:\mathrm{consists}\:\mathrm{of}\:\mathrm{6} \\ $$$$\mathrm{triangles}\:\mathrm{of}\:\mathrm{unit}\:\mathrm{side}. \\ $$$$\mathrm{Area}\:\mathrm{of}\:\:\mathrm{triangle}\:\mathrm{of}\:\mathrm{unit}\:\mathrm{side}\left(\blacktriangle\right)\:: \\ $$$$\:\:\:\:\:\:\:\blacktriangle=\sqrt{\frac{\mathrm{3}}{\mathrm{2}}\left(\frac{\mathrm{3}}{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{3}} }=\sqrt{\frac{\mathrm{3}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} }} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\frac{\sqrt{\mathrm{3}}}{\mathrm{4}} \\ $$$$\mathrm{Area}\:\mathrm{of}\:\mathrm{hexagon}\:\mathrm{of}\:\mathrm{unit}\:\mathrm{side}\:\left(\mathrm{A}\right):\:\:\: \\ $$$$\:\:\:\:\:\:\mathrm{A}=\mathrm{6}\blacktriangle=\mathrm{6}×\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}=\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}}=\sqrt{\frac{\mathrm{27}}{\mathrm{4}}} \\ $$$$\mathrm{Square}\:\mathrm{of}\:\mathrm{area}\:\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}}\:\mathrm{has}\:\mathrm{its}\:\mathrm{side}\left(\mathrm{s}\right)\:\mathrm{equal}\:\mathrm{to} \\ $$$$\:\:\:\:\:\:\:\:\sqrt{\sqrt{\frac{\mathrm{27}}{\mathrm{4}}}} \\ $$$$\mathrm{So}\:\mathrm{ultimately}\:\mathrm{we}\:\mathrm{need}\:\mathrm{to}\:\mathrm{draw}\:\mathrm{a}\:\mathrm{line}\:\mathrm{segment}\:\mathrm{of} \\ $$$$\mathrm{measure}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\sqrt{\sqrt{\frac{\mathrm{27}}{\mathrm{4}}}}\:\:\:\:\:\mathrm{units} \\ $$$$\mathrm{One}\:\mathrm{way}\:\mathrm{may}\:\mathrm{be}\:\mathrm{as}\:\mathrm{under}: \\ $$$$\bullet\mathrm{Extend}\:\mathrm{the}\:\mathrm{side}\:\mathrm{of}\:\mathrm{hexagon}\:\mathrm{27}\:\mathrm{times}.\:\mathrm{Say}\:\mathrm{it}\:\mathrm{AB} \\ $$$$\bullet\:\mathrm{Cut}\:\mathrm{off}\:\mathrm{AC}=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{AB}\:\:. \\ $$$$\bullet\mathrm{Cut}\:\mathrm{off}\:\mathrm{CD}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{hexagon}\:\mathrm{side}\:\mathrm{from}\:\mathrm{AB}. \\ $$$$\mathrm{Continue} \\ $$

Answered by Rasheed Soomro last updated on 19/Dec/15

∗Let AB is a side of hexagon measuring 1 unit. •Draw a line l perpendicular to AB through A (or B) •Cut off AC = 6 AB , CD=AB on one side of AB and AE = AB on the other side.( AC , CD and AE don′t overlap one another.) •Take a point F on CD so that CF=(3/4) CD ∗AF=AC+CF=6+(3/4)=((27)/4) ∗EF=AF+EA=((27)/4)+1. •Draw semi circle on EF on the side of B •Produce AB to meet the semicircle say at G. ∗ AG=(√((27)/4)) . •Produce AB on the side of A and cut off AH = AB ∗HG=AG+AH=(√((27)/4))+1 • Draw semicircle on HG. Let the line l meets the semicircle at I. ∗AI=(√(√(((27)/4) ))) •Taking AI as side of the square complet the square. ∗Area of the square will be ((√(√(((27)/4) ))))^2 =(√((27)/4)) which is also the area of the given hexagon. See comment also.

$$\ast{Let}\:{AB}\:{is}\:{a}\:{side}\:{of}\:{hexagon}\:{measuring} \\ $$$$\mathrm{1}\:{unit}. \\ $$$$\bullet{Draw}\:{a}\:{line}\:{l}\:\:{perpendicular}\:{to}\:{AB}\:{through} \\ $$$${A}\:\left({or}\:{B}\right)\: \\ $$$$\bullet{Cut}\:{off}\:\:{AC}\:=\:\mathrm{6}\:{AB}\:\:,\:{CD}={AB}\:\:\:{on}\:{one} \\ $$$$\:{side}\:{of}\:{AB}\:\:{and}\:{AE}\:=\:{AB}\:{on}\:{the}\:{other} \\ $$$${side}.\left(\:{AC}\:,\:{CD}\:{and}\:{AE}\:{don}'{t}\:{overlap}\right. \\ $$$$\left.{one}\:{another}.\right)\: \\ $$$$\bullet{Take}\:{a}\:{point}\:{F}\:{on}\:{CD}\:{so}\:{that}\:{CF}=\frac{\mathrm{3}}{\mathrm{4}}\:{CD} \\ $$$$\ast{AF}={AC}+{CF}=\mathrm{6}+\frac{\mathrm{3}}{\mathrm{4}}=\frac{\mathrm{27}}{\mathrm{4}} \\ $$$$\ast{EF}={AF}+{EA}=\frac{\mathrm{27}}{\mathrm{4}}+\mathrm{1}. \\ $$$$\bullet{Draw}\:{semi}\:{circle}\:{on}\:{EF}\:\:{on}\:{the}\:{side}\:{of}\:{B} \\ $$$$\bullet{Produce}\:{AB}\:{to}\:{meet}\:{the}\:{semicircle}\:{say}\:{at}\:{G}. \\ $$$$\ast\:{AG}=\sqrt{\frac{\mathrm{27}}{\mathrm{4}}}\:. \\ $$$$\bullet{Produce}\:{AB}\:{on}\:{the}\:{side}\:{of}\:{A}\:{and}\:{cut}\:{off}\: \\ $$$${AH}\:=\:{AB} \\ $$$$\ast{HG}={AG}+{AH}=\sqrt{\frac{\mathrm{27}}{\mathrm{4}}}+\mathrm{1} \\ $$$$\bullet\:{Draw}\:{semicircle}\:{on}\:{HG}.\:{Let}\:{the}\:{line}\:{l}\:{meets} \\ $$$${the}\:{semicircle}\:{at}\:{I}. \\ $$$$\ast{AI}=\sqrt{\sqrt{\frac{\mathrm{27}}{\mathrm{4}}\:}} \\ $$$$\bullet{Taking}\:{AI}\:{as}\:{side}\:{of}\:{the}\:{square}\:{complet}\:{the} \\ $$$${square}. \\ $$$$\ast{Area}\:{of}\:{the}\:{square}\:{will}\:{be}\:\left(\sqrt{\sqrt{\frac{\mathrm{27}}{\mathrm{4}}\:}}\right)^{\mathrm{2}} =\sqrt{\frac{\mathrm{27}}{\mathrm{4}}} \\ $$$${which}\:{is}\:{also}\:{the}\:{area}\:{of}\:{the}\:{given}\:{hexagon}. \\ $$$${See}\:{comment}\:{also}. \\ $$$$ \\ $$

Commented by Rasheed Soomro last updated on 17/Dec/15

n−gon can be squared only when sin ((2π)/n) can be expressed as rationals or surds containing only squareroots.

$${n}−{gon}\:\:{can}\:{be}\:\boldsymbol{\mathrm{squared}}\:{only}\:{when}\:\mathrm{sin}\:\frac{\mathrm{2}\pi}{{n}}\:{can} \\ $$$${be}\:{expressed}\:\:{as}\:{rationals}\:{or}\:{surds}\:{containing} \\ $$$${only}\:{squareroots}. \\ $$

Commented by prakash jain last updated on 17/Dec/15

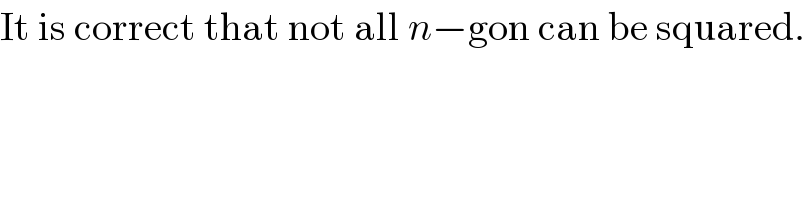
It is correct that not all n−gon can be squared.

$$\mathrm{It}\:\mathrm{is}\:\mathrm{correct}\:\mathrm{that}\:\mathrm{not}\:\mathrm{all}\:{n}−\mathrm{gon}\:\mathrm{can}\:\mathrm{be}\:\mathrm{squared}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com