Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 36442 by abdo mathsup 649 cc last updated on 02/Jun/18

let f(x)= (√(2+x^2 )) −x 1) calculate lim_(x→+∞) f(x) and lim_(x→−∞) f(x) 2) calculate lim_(x→+∞) ((f(x))/x) and lim_(x→−∞) ((f(x))/x) 3) calculate f^′ (x) and determine its sign 4) give the variation of 5) give the equation of assymptote at point A(1,f(1)) 6) find f^(−1) (x) and calculate (f^(−1) )^′ (x) 7) calculate ∫_0 ^4 f(x)dx .

$${let}\:{f}\left({x}\right)=\:\sqrt{\mathrm{2}+{x}^{\mathrm{2}} \:}\:\:\:−{x} \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:{lim}_{{x}\rightarrow+\infty} {f}\left({x}\right)\:{and}\:{lim}_{{x}\rightarrow−\infty} {f}\left({x}\right) \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:{lim}_{{x}\rightarrow+\infty} \:\frac{{f}\left({x}\right)}{{x}}\:{and}\:\:{lim}_{{x}\rightarrow−\infty} \:\frac{{f}\left({x}\right)}{{x}} \\ $$$$\left.\mathrm{3}\right)\:{calculate}\:{f}^{'} \left({x}\right)\:{and}\:{determine}\:{its}\:{sign} \\ $$$$\left.\mathrm{4}\right)\:{give}\:{the}\:{variation}\:{of} \\ $$$$\left.\mathrm{5}\right)\:{give}\:{the}\:{equation}\:{of}\:{assymptote}\:{at}\:\:{point} \\ $$$${A}\left(\mathrm{1},{f}\left(\mathrm{1}\right)\right) \\ $$$$\left.\mathrm{6}\right)\:{find}\:{f}^{−\mathrm{1}} \left({x}\right)\:{and}\:{calculate}\:\left({f}^{−\mathrm{1}} \right)^{'} \left({x}\right) \\ $$$$\left.\mathrm{7}\right)\:{calculate}\:\:\int_{\mathrm{0}} ^{\mathrm{4}} {f}\left({x}\right){dx}\:. \\ $$

Commented by abdo.msup.com last updated on 05/Jun/18

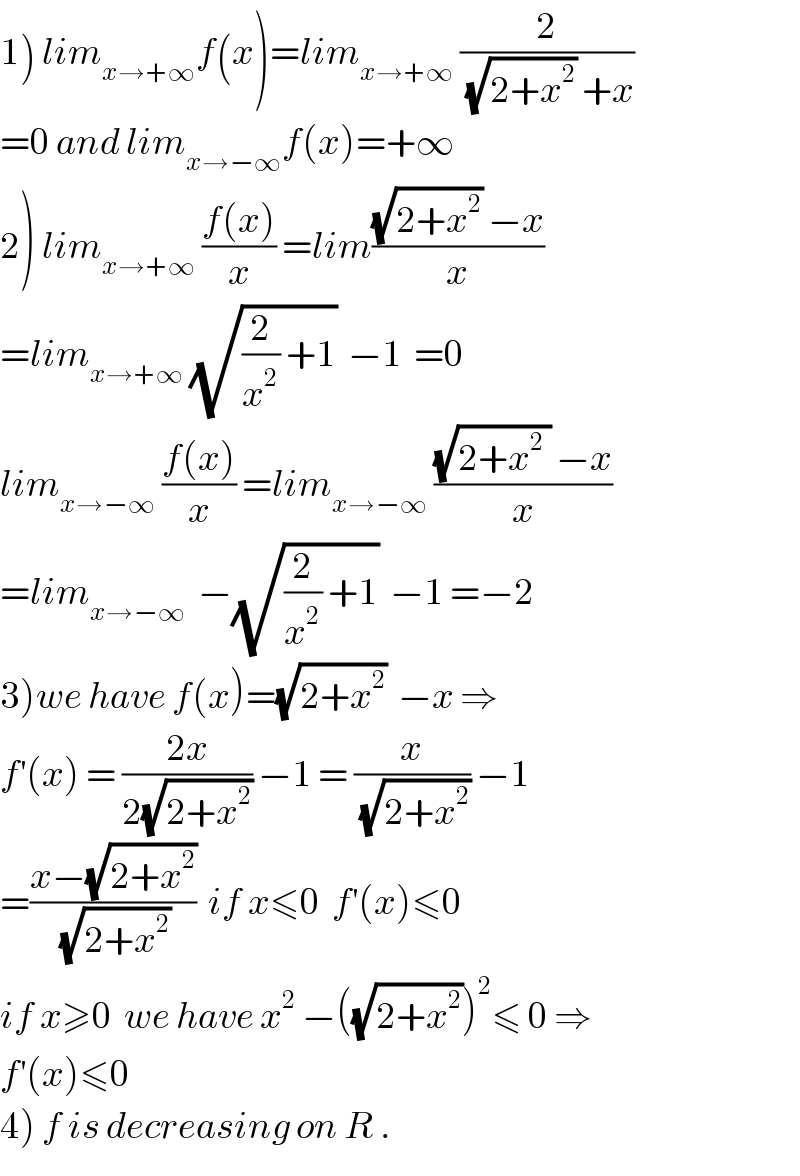
1) lim_(x→+∞) f(x)=lim_(x→+∞) (2/((√(2+x^2 )) +x)) =0 and lim_(x→−∞) f(x)=+∞ 2) lim_(x→+∞) ((f(x))/x) =lim(((√(2+x^2 )) −x)/x) =lim_(x→+∞) (√((2/x^2 ) +1)) −1 =0 lim_(x→−∞) ((f(x))/x) =lim_(x→−∞) (((√(2+x^2 )) −x)/x) =lim_(x→−∞) −(√((2/x^2 ) +1)) −1 =−2 3)we have f(x)=(√(2+x^2 )) −x ⇒ f^′ (x) = ((2x)/(2(√(2+x^2 )))) −1 = (x/(√(2+x^2 ))) −1 =((x−(√(2+x^2 )))/(√(2+x^2 ))) if x≤0 f^′ (x)≤0 if x≥0 we have x^2 −((√(2+x^2 )))^2 ≤ 0 ⇒ f^′ (x)≤0 4) f is decreasing on R .

$$\left.\mathrm{1}\right)\:{lim}_{{x}\rightarrow+\infty} {f}\left({x}\right)={lim}_{{x}\rightarrow+\infty} \:\frac{\mathrm{2}}{\sqrt{\mathrm{2}+{x}^{\mathrm{2}} }\:+{x}} \\ $$$$=\mathrm{0}\:{and}\:{lim}_{{x}\rightarrow−\infty} {f}\left({x}\right)=+\infty \\ $$$$\left.\mathrm{2}\right)\:{lim}_{{x}\rightarrow+\infty} \:\frac{{f}\left({x}\right)}{{x}}\:={lim}\frac{\sqrt{\mathrm{2}+{x}^{\mathrm{2}} }\:−{x}}{{x}} \\ $$$$={lim}_{{x}\rightarrow+\infty} \:\sqrt{\frac{\mathrm{2}}{{x}^{\mathrm{2}} }\:+\mathrm{1}}\:\:−\mathrm{1}\:\:=\mathrm{0} \\ $$$${lim}_{{x}\rightarrow−\infty} \:\frac{{f}\left({x}\right)}{{x}}\:={lim}_{{x}\rightarrow−\infty} \:\frac{\sqrt{\mathrm{2}+{x}^{\mathrm{2}} \:}\:−{x}}{{x}} \\ $$$$={lim}_{{x}\rightarrow−\infty} \:\:−\sqrt{\frac{\mathrm{2}}{{x}^{\mathrm{2}} }\:+\mathrm{1}}\:\:−\mathrm{1}\:=−\mathrm{2} \\ $$$$\left.\mathrm{3}\right){we}\:{have}\:{f}\left({x}\right)=\sqrt{\mathrm{2}+{x}^{\mathrm{2}} }\:\:−{x}\:\Rightarrow \\ $$$${f}^{'} \left({x}\right)\:=\:\frac{\mathrm{2}{x}}{\mathrm{2}\sqrt{\mathrm{2}+{x}^{\mathrm{2}} }}\:−\mathrm{1}\:=\:\frac{{x}}{\sqrt{\mathrm{2}+{x}^{\mathrm{2}} }}\:−\mathrm{1} \\ $$$$=\frac{{x}−\sqrt{\mathrm{2}+{x}^{\mathrm{2}} }}{\sqrt{\mathrm{2}+{x}^{\mathrm{2}} }}\:\:{if}\:{x}\leqslant\mathrm{0}\:\:{f}^{'} \left({x}\right)\leqslant\mathrm{0}\: \\ $$$${if}\:{x}\geqslant\mathrm{0}\:\:{we}\:{have}\:{x}^{\mathrm{2}} \:−\left(\sqrt{\mathrm{2}+{x}^{\mathrm{2}} }\right)^{\mathrm{2}} \leqslant\:\mathrm{0}\:\Rightarrow \\ $$$${f}^{'} \left({x}\right)\leqslant\mathrm{0} \\ $$$$\left.\mathrm{4}\right)\:{f}\:{is}\:{decreasing}\:{on}\:{R}\:. \\ $$

Commented by abdo.msup.com last updated on 05/Jun/18

5) we have f(x)=(√(2+x^2 )) −x ⇒ f(1)=(√3) −1 also f^′ (x)= (x/(√(2+x^2 ))) −1 ⇒ f^′ (1) = (1/(√3)) −1 so the equstion of assymptote is y =f^′ (1)(x−1) +f(1)⇒ y =((1/(√3)) −1)(x−1) +(√3) −1 .

$$\left.\mathrm{5}\right)\:{we}\:{have}\:\:{f}\left({x}\right)=\sqrt{\mathrm{2}+{x}^{\mathrm{2}} }\:−{x}\:\Rightarrow \\ $$$${f}\left(\mathrm{1}\right)=\sqrt{\mathrm{3}}\:−\mathrm{1}\:{also}\:{f}^{'} \left({x}\right)=\:\frac{{x}}{\sqrt{\mathrm{2}+{x}^{\mathrm{2}} }}\:−\mathrm{1}\:\Rightarrow \\ $$$${f}^{'} \left(\mathrm{1}\right)\:=\:\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\:−\mathrm{1}\:{so}\:{the}\:{equstion}\:{of}\: \\ $$$${assymptote}\:{is} \\ $$$${y}\:={f}^{'} \left(\mathrm{1}\right)\left({x}−\mathrm{1}\right)\:+{f}\left(\mathrm{1}\right)\Rightarrow \\ $$$${y}\:=\left(\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\:−\mathrm{1}\right)\left({x}−\mathrm{1}\right)\:+\sqrt{\mathrm{3}}\:−\mathrm{1}\:. \\ $$

Commented by abdo.msup.com last updated on 05/Jun/18

6) f is decreasing so f]−∞,+∞[ =]f(+∞),f(−∞)[=]0,+∞[ f is a bijection from R to ]0,+∞[ let f(x)=y ⇔ (√(2+x^2 )) −x =y ⇒ (√(2+x^2 )) =x +y ( so x+y>0)⇒ 2+x^2 =x^2 +2xy +y^2 ⇒ 2=2xy +y^2 ⇒ 2−y^2 =2xy ⇒x=((2−y^2 )/(2y)) ⇒ f^(−1) (x) = ((2−x^2 )/(2x)) and x>0

$$\left.\mathrm{6}\left.\right)\:{f}\:{is}\:{decreasing}\:{so}\:{f}\right]−\infty,+\infty\left[\right. \\ $$$$\left.=\right]{f}\left(+\infty\right),{f}\left(−\infty\right)\left[=\right]\mathrm{0},+\infty\left[\:{f}\:{is}\right. \\ $$$$\left.{a}\:{bijection}\:{from}\:{R}\:{to}\:\right]\mathrm{0},+\infty\left[\right. \\ $$$${let}\:{f}\left({x}\right)={y}\:\Leftrightarrow\:\sqrt{\mathrm{2}+{x}^{\mathrm{2}} }\:−{x}\:={y}\:\Rightarrow \\ $$$$\sqrt{\mathrm{2}+{x}^{\mathrm{2}} }\:={x}\:+{y}\:\:\left(\:{so}\:{x}+{y}>\mathrm{0}\right)\Rightarrow \\ $$$$\mathrm{2}+{x}^{\mathrm{2}} \:={x}^{\mathrm{2}} \:+\mathrm{2}{xy}\:+{y}^{\mathrm{2}} \:\Rightarrow \\ $$$$\mathrm{2}=\mathrm{2}{xy}\:+{y}^{\mathrm{2}} \:\Rightarrow\:\mathrm{2}−{y}^{\mathrm{2}} \:=\mathrm{2}{xy}\:\Rightarrow{x}=\frac{\mathrm{2}−{y}^{\mathrm{2}} }{\mathrm{2}{y}} \\ $$$$\Rightarrow\:{f}^{−\mathrm{1}} \left({x}\right)\:=\:\frac{\mathrm{2}−{x}^{\mathrm{2}} }{\mathrm{2}{x}}\:\:{and}\:{x}>\mathrm{0}\: \\ $$

Commented by abdo.msup.com last updated on 05/Jun/18

we have f^(−1) (x)= (1/x) −(x/2) ⇒ (f^(−1) (x))^′ = −(1/x^2 ) −(1/2) .

$${we}\:{have}\:{f}^{−\mathrm{1}} \left({x}\right)=\:\frac{\mathrm{1}}{{x}}\:−\frac{{x}}{\mathrm{2}}\:\Rightarrow \\ $$$$\left({f}^{−\mathrm{1}} \left({x}\right)\right)^{'} \:=\:−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:−\frac{\mathrm{1}}{\mathrm{2}}\:. \\ $$

Commented by abdo.msup.com last updated on 05/Jun/18

7) let A= ∫_0 ^4 f(x)dx A = ∫_0 ^4 ((√(2+x^2 )) −x)dx =∫_0 ^4 (√(2+x^2 )) dx −[(x^2 /2)]_0 ^4 =∫_0 ^4 (√(2+x^2 ))dx −8 but chang.x=(√2) sh(t) give ∫_0 ^4 (√(2+x^2 ))dx=(√2) ∫_0 ^(argsh((4/(√2)))) ch(t)(√2)chtdt = 2 ∫_0 ^(argsh((4/(√2)))) ch^2 (t)dt =2 ∫_0 ^(argsh((4/(√2)))) ((1+ch(2t))/2)dt =argsh((4/(√2))) +(1/2)[sh(2t)]_0 ^(argsh((4/(√2)))) =ln( (4/(√2)) +3) +(1/2)sh(2 ln{(4/(√2)) +3)}) =ln((4/(√2)) +3) +(1/4){ ((4/(√2)) +3)^2 +((4/(√2)) +3)^(−1) } .

$$\left.\mathrm{7}\right)\:{let}\:{A}=\:\int_{\mathrm{0}} ^{\mathrm{4}} \:{f}\left({x}\right){dx} \\ $$$${A}\:\:=\:\int_{\mathrm{0}} ^{\mathrm{4}} \:\left(\sqrt{\mathrm{2}+{x}^{\mathrm{2}} }\:−{x}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{4}} \:\sqrt{\mathrm{2}+{x}^{\mathrm{2}} }\:{dx}\:\:−\left[\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right]_{\mathrm{0}} ^{\mathrm{4}} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{4}} \sqrt{\mathrm{2}+{x}^{\mathrm{2}} \:}{dx}\:−\mathrm{8}\:\:{but}\:{chang}.{x}=\sqrt{\mathrm{2}}\:{sh}\left({t}\right) \\ $$$${give} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{4}} \:\sqrt{\mathrm{2}+{x}^{\mathrm{2}} }{dx}=\sqrt{\mathrm{2}}\:\int_{\mathrm{0}} ^{{argsh}\left(\frac{\mathrm{4}}{\sqrt{\mathrm{2}}}\right)} \:{ch}\left({t}\right)\sqrt{\mathrm{2}}{chtdt} \\ $$$$=\:\mathrm{2}\:\int_{\mathrm{0}} ^{{argsh}\left(\frac{\mathrm{4}}{\sqrt{\mathrm{2}}}\right)} \:{ch}^{\mathrm{2}} \left({t}\right){dt}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{{argsh}\left(\frac{\mathrm{4}}{\sqrt{\mathrm{2}}}\right)} \frac{\mathrm{1}+{ch}\left(\mathrm{2}{t}\right)}{\mathrm{2}}{dt} \\ $$$$={argsh}\left(\frac{\mathrm{4}}{\sqrt{\mathrm{2}}}\right)\:\:+\frac{\mathrm{1}}{\mathrm{2}}\left[{sh}\left(\mathrm{2}{t}\right)\right]_{\mathrm{0}} ^{{argsh}\left(\frac{\mathrm{4}}{\sqrt{\mathrm{2}}}\right)} \\ $$$$\left.={ln}\left(\:\frac{\mathrm{4}}{\sqrt{\mathrm{2}}}\:+\mathrm{3}\right)\:+\frac{\mathrm{1}}{\mathrm{2}}{sh}\left(\mathrm{2}\:{ln}\left\{\frac{\mathrm{4}}{\sqrt{\mathrm{2}}}\:+\mathrm{3}\right)\right\}\right) \\ $$$$={ln}\left(\frac{\mathrm{4}}{\sqrt{\mathrm{2}}}\:+\mathrm{3}\right)\:+\frac{\mathrm{1}}{\mathrm{4}}\left\{\:\left(\frac{\mathrm{4}}{\sqrt{\mathrm{2}}}\:+\mathrm{3}\right)^{\mathrm{2}} \:+\left(\frac{\mathrm{4}}{\sqrt{\mathrm{2}}}\:+\mathrm{3}\right)^{−\mathrm{1}} \right\}\:. \\ $$$$ \\ $$

Commented by abdo.msup.com last updated on 05/Jun/18

I =ln(4+3(√2)) −(1/2)ln(2) +(1/4){ ((4/(√2)) +3)^2 −((4/(√2)) +3)^(−2) } −8 .

$${I}\:={ln}\left(\mathrm{4}+\mathrm{3}\sqrt{\mathrm{2}}\right)\:−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{2}\right) \\ $$$$+\frac{\mathrm{1}}{\mathrm{4}}\left\{\:\left(\frac{\mathrm{4}}{\sqrt{\mathrm{2}}}\:+\mathrm{3}\right)^{\mathrm{2}} \:−\left(\frac{\mathrm{4}}{\sqrt{\mathrm{2}}}\:+\mathrm{3}\right)^{−\mathrm{2}} \right\}\:−\mathrm{8}\:. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com