Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 36444 by rahul 19 last updated on 02/Jun/18

∫ (dx/((2x−7)(√((x−3)(x−4))))) = ?

$$\int\:\frac{\mathrm{d}{x}}{\left(\mathrm{2}{x}−\mathrm{7}\right)\sqrt{\left({x}−\mathrm{3}\right)\left({x}−\mathrm{4}\right)}}\:=\:? \\ $$

Commented by math1967 last updated on 02/Jun/18

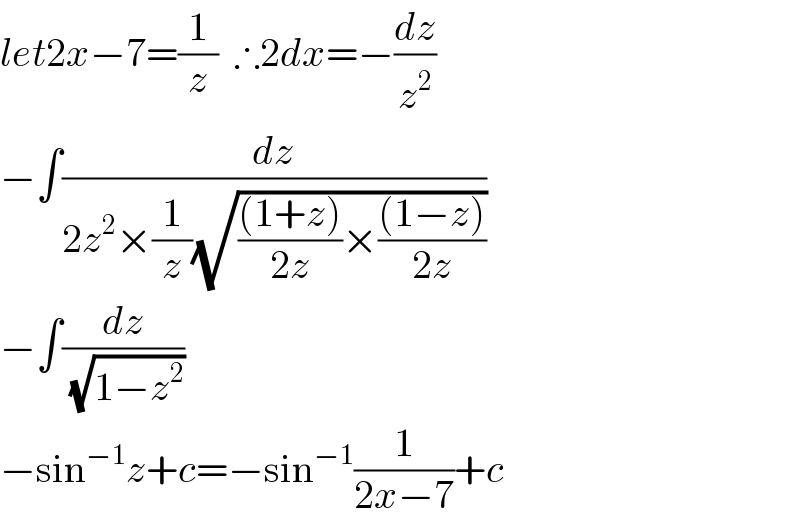
let2x−7=(1/z) ∴2dx=−(dz/z^2 ) −∫(dz/(2z^2 ×(1/z)(√((((1+z))/(2z))×(((1−z))/(2z)))))) −∫(dz/(√(1−z^2 ))) −sin^(−1) z+c=−sin^(−1) (1/(2x−7))+c

$${let}\mathrm{2}{x}−\mathrm{7}=\frac{\mathrm{1}}{{z}}\:\:\therefore\mathrm{2}{dx}=−\frac{{dz}}{{z}^{\mathrm{2}} } \\ $$$$−\int\frac{{dz}}{\mathrm{2}{z}^{\mathrm{2}} ×\frac{\mathrm{1}}{{z}}\sqrt{\frac{\left(\mathrm{1}+{z}\right)}{\mathrm{2}{z}}×\frac{\left(\mathrm{1}−{z}\right)}{\mathrm{2}{z}}}} \\ $$$$−\int\frac{{dz}}{\sqrt{\mathrm{1}−{z}^{\mathrm{2}} }} \\ $$$$−\mathrm{sin}^{−\mathrm{1}} {z}+{c}=−\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}{x}−\mathrm{7}}+{c} \\ $$

Commented by math1967 last updated on 02/Jun/18

Am I correct?

$${Am}\:{I}\:{correct}? \\ $$

Commented by MJS last updated on 02/Jun/18

indeed correct!

$$\mathrm{indeed}\:\mathrm{correct}! \\ $$

Commented by rahul 19 last updated on 02/Jun/18

Thanks for confirming!

$$\mathrm{Thanks}\:\mathrm{for}\:\mathrm{confirming}! \\ $$

Commented by MJS last updated on 02/Jun/18

another way: ∫(dx/((2x−7)(√(x^2 −7x+12))))= [t=(√(x^2 −7x+12)) → dx=((2(√(x^2 −7x+12)))/(2x−7))dt] =2∫(dt/(4t^2 +1))= [u=2t → dt=(du/2)] =∫(du/(u^2 +1))=arctan u=arctan 2t= =arctan 2(√((x−3)(x−4)))+C

$$\mathrm{another}\:\mathrm{way}: \\ $$$$\int\frac{{dx}}{\left(\mathrm{2}{x}−\mathrm{7}\right)\sqrt{{x}^{\mathrm{2}} −\mathrm{7}{x}+\mathrm{12}}}= \\ $$$$\:\:\:\:\:\left[{t}=\sqrt{{x}^{\mathrm{2}} −\mathrm{7}{x}+\mathrm{12}}\:\rightarrow\:{dx}=\frac{\mathrm{2}\sqrt{{x}^{\mathrm{2}} −\mathrm{7}{x}+\mathrm{12}}}{\mathrm{2}{x}−\mathrm{7}}{dt}\right] \\ $$$$=\mathrm{2}\int\frac{{dt}}{\mathrm{4}{t}^{\mathrm{2}} +\mathrm{1}}= \\ $$$$\:\:\:\:\:\left[{u}=\mathrm{2}{t}\:\rightarrow\:{dt}=\frac{{du}}{\mathrm{2}}\right] \\ $$$$=\int\frac{{du}}{{u}^{\mathrm{2}} +\mathrm{1}}=\mathrm{arctan}\:{u}=\mathrm{arctan}\:\mathrm{2}{t}= \\ $$$$=\mathrm{arctan}\:\mathrm{2}\sqrt{\left({x}−\mathrm{3}\right)\left({x}−\mathrm{4}\right)}+{C} \\ $$

Commented by math1967 last updated on 02/Jun/18

It is more easy.Thanks sir

$${It}\:{is}\:{more}\:{easy}.{Thanks}\:{sir} \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 02/Jun/18

(x−3)(x−4)=x^2 −7x+12 not x^2 +7x+12

$$\left({x}−\mathrm{3}\right)\left({x}−\mathrm{4}\right)={x}^{\mathrm{2}} −\mathrm{7}{x}+\mathrm{12}\:\:\:{not}\:{x}^{\mathrm{2}} +\mathrm{7}{x}+\mathrm{12} \\ $$

Commented by math1967 last updated on 02/Jun/18

you are correct Tanmay sir

$${you}\:{are}\:{correct}\:{Tanmay}\:{sir} \\ $$

Commented by MJS last updated on 02/Jun/18

sorry, typo. I corrected it

$$\mathrm{sorry},\:\mathrm{typo}.\:\mathrm{I}\:\mathrm{corrected}\:\mathrm{it} \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 02/Jun/18

Commented by prof Abdo imad last updated on 03/Jun/18

changement 2x−7=t give I = ∫ (1/(t(√((((t+7)/2)−3)(((t+7)/2) −4)))))(dt/2) = (1/2)∫ ((2dt)/(t(√((t+1)(t−1))))) = ∫ (dt/(t(√(t^2 −1)))) and changement t =ch(u) give I = ∫ ((sh(u))/(ch(u)shu))du = ∫ (du/(chu)) =∫ ((2du)/(e^u +e^(−u) )) =_(e^u =x) ∫ (2/(x +(1/x))) (dx/x) = 2 ∫ (dx/(x^2 +1)) = 2arctanx +c =2arctan( e^u ) = 2arctan ( e^(argch(t)) ) +c = 2arctan (ln(t +(√(t^2 −1))) +c =2arctan{ln(2x−7 +(√((2x−7)^2 −1)))} +c .

$${changement}\:\:\mathrm{2}{x}−\mathrm{7}={t}\:{give} \\ $$$${I}\:=\:\int\:\:\:\:\:\:\frac{\mathrm{1}}{{t}\sqrt{\left(\frac{{t}+\mathrm{7}}{\mathrm{2}}−\mathrm{3}\right)\left(\frac{{t}+\mathrm{7}}{\mathrm{2}}\:−\mathrm{4}\right)}}\frac{{dt}}{\mathrm{2}} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\:\frac{\mathrm{2}{dt}}{{t}\sqrt{\left({t}+\mathrm{1}\right)\left({t}−\mathrm{1}\right)}} \\ $$$$=\:\int\:\:\:\:\:\frac{{dt}}{{t}\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}}\:{and}\:{changement}\:{t}\:={ch}\left({u}\right)\:{give} \\ $$$${I}\:=\:\int\:\:\:\:\:\frac{{sh}\left({u}\right)}{{ch}\left({u}\right){shu}}{du}\:=\:\int\:\:\:\:\:\frac{{du}}{{chu}} \\ $$$$=\int\:\:\:\:\frac{\mathrm{2}{du}}{{e}^{{u}} \:+{e}^{−{u}} }\:=_{{e}^{{u}} ={x}} \:\:\int\:\:\:\:\:\frac{\mathrm{2}}{{x}\:+\frac{\mathrm{1}}{{x}}}\:\frac{{dx}}{{x}} \\ $$$$=\:\mathrm{2}\:\int\:\:\:\:\frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{1}}\:=\:\mathrm{2}{arctanx}\:+{c} \\ $$$$=\mathrm{2}{arctan}\left(\:{e}^{{u}} \right)\:=\:\mathrm{2}{arctan}\:\left(\:{e}^{{argch}\left({t}\right)} \right)\:+{c} \\ $$$$=\:\mathrm{2}{arctan}\:\left({ln}\left({t}\:+\sqrt{\left.{t}^{\mathrm{2}} −\mathrm{1}\right)}\:\:+{c}\right.\right. \\ $$$$=\mathrm{2}{arctan}\left\{{ln}\left(\mathrm{2}{x}−\mathrm{7}\:+\sqrt{\left.\left(\mathrm{2}{x}−\mathrm{7}\right)^{\mathrm{2}} \:−\mathrm{1}\right)}\right\}\:+{c}\:.\right. \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com