Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 36459 by rahul 19 last updated on 02/Jun/18

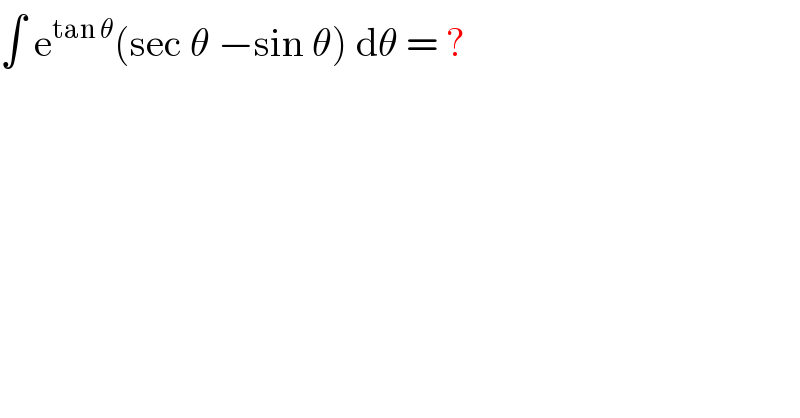
∫ e^(tan θ) (sec θ −sin θ) dθ = ?

$$\int\:\mathrm{e}^{\mathrm{tan}\:\theta} \left(\mathrm{sec}\:\theta\:−\mathrm{sin}\:\theta\right)\:\mathrm{d}\theta\:=\:? \\ $$

Answered by ajfour last updated on 02/Jun/18

let tan θ=t ⇒ I=∫e^t (sec θ−sin θ)cos^2 θdt =∫e^t (cos θ−((sin θ)/(1+tan^2 θ)))dt =∫e^t ((1/(√(1+t^2 )))−(t/((1+t^2 )^(3/2) )))dt =∫e^t [(1/(√(1+t^2 )))+(d/dt)((1/(√(1+t^2 ))))]dt = (e^t /(√(1+t^2 )))+c I = e^(tan θ) cos θ +c .

$${let}\:\mathrm{tan}\:\theta={t} \\ $$$$\Rightarrow\:{I}=\int{e}^{{t}} \left(\mathrm{sec}\:\theta−\mathrm{sin}\:\theta\right)\mathrm{cos}\:^{\mathrm{2}} \theta{dt} \\ $$$$\:\:\:\:\:\:\:\:=\int{e}^{{t}} \left(\mathrm{cos}\:\theta−\frac{\mathrm{sin}\:\theta}{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \theta}\right){dt} \\ $$$$\:\:\:\:\:\:\:=\int{e}^{{t}} \left(\frac{\mathrm{1}}{\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}−\frac{{t}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} }\right){dt} \\ $$$$\:\:\:\:\:\:=\int{e}^{{t}} \left[\frac{\mathrm{1}}{\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}+\frac{{d}}{{dt}}\left(\frac{\mathrm{1}}{\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}\right)\right]{dt} \\ $$$$\:\:\:\:\:\:=\:\frac{{e}^{{t}} }{\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}+{c} \\ $$$$\:\:\:\:\:{I}\:=\:{e}^{\mathrm{tan}\:\theta} \mathrm{cos}\:\theta\:+{c}\:. \\ $$

Commented by rahul 19 last updated on 02/Jun/18

Thank you sir ����

Answered by MJS last updated on 02/Jun/18

lol, tricky... ∫e^(tan θ) (sec θ−sin θ)dθ= =∫e^(tan θ) sec θ dθ−∫e^(tan θ) sin θ dθ= [((f′=sin θ ⇒ f=−cos θ)),((g=e^(tan θ) ⇒ g′=e^(tan θ) sec^2 θ)),((∫f′g=fg−∫fg′)) ] =∫e^(tan θ) sec θ dθ+e^(tan θ) cos θ−∫e^(tan θ) cos θ sec^2 θ dθ= =e^(tan θ) cos θ +C

$$\mathrm{lol},\:\mathrm{tricky}... \\ $$$$\int\mathrm{e}^{\mathrm{tan}\:\theta} \left(\mathrm{sec}\:\theta−\mathrm{sin}\:\theta\right){d}\theta= \\ $$$$=\int\mathrm{e}^{\mathrm{tan}\:\theta} \mathrm{sec}\:\theta\:{d}\theta−\int\mathrm{e}^{\mathrm{tan}\:\theta} \mathrm{sin}\:\theta\:{d}\theta= \\ $$$$\:\:\:\:\:\begin{bmatrix}{{f}'=\mathrm{sin}\:\theta\:\Rightarrow\:{f}=−\mathrm{cos}\:\theta}\\{{g}=\mathrm{e}^{\mathrm{tan}\:\theta} \:\Rightarrow\:{g}'=\mathrm{e}^{\mathrm{tan}\:\theta} \mathrm{sec}^{\mathrm{2}} \:\theta}\\{\int{f}'{g}={fg}−\int{fg}'}\end{bmatrix} \\ $$$$=\int\mathrm{e}^{\mathrm{tan}\:\theta} \mathrm{sec}\:\theta\:{d}\theta+\mathrm{e}^{\mathrm{tan}\:\theta} \mathrm{cos}\:\theta−\int\mathrm{e}^{\mathrm{tan}\:\theta} \mathrm{cos}\:\theta\:\mathrm{sec}^{\mathrm{2}} \:\theta\:{d}\theta= \\ $$$$=\mathrm{e}^{\mathrm{tan}\:\theta} \mathrm{cos}\:\theta\:+{C} \\ $$

Commented by rahul 19 last updated on 02/Jun/18

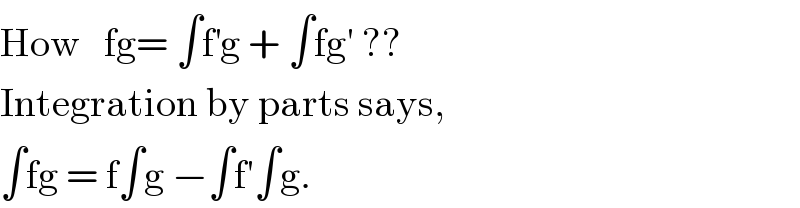
How fg= ∫f^′ g + ∫fg′ ?? Integration by parts says, ∫fg = f∫g −∫f′∫g.

$$\mathrm{How}\:\:\:\mathrm{fg}=\:\int\mathrm{f}^{'} \mathrm{g}\:+\:\int\mathrm{fg}'\:?? \\ $$$$\mathrm{Integration}\:\mathrm{by}\:\mathrm{parts}\:\mathrm{says}, \\ $$$$\int\mathrm{fg}\:=\:\mathrm{f}\int\mathrm{g}\:−\int\mathrm{f}'\int\mathrm{g}. \\ $$

Commented by MJS last updated on 02/Jun/18

https://en.wikipedia.org/wiki/Integration_by_parts

$${https}://{en}.{wikipedia}.{org}/{wiki}/{Integration\_by\_parts} \\ $$

Commented by rahul 19 last updated on 02/Jun/18

Sir if you want to integrate say ∫xsin x then g=sin x , f=x . (ILATE ) ⇒ ∫g= −cos x , f′ = 1. ∫fg= f∫g − ∫f′ ∫g ⇒ x(−cos x) − ∫−(cos x) ⇒ −xcos x+sin x+c.

$$\mathrm{Sir}\:\mathrm{if}\:\mathrm{you}\:\mathrm{want}\:\mathrm{to}\:\mathrm{integrate}\:\mathrm{say} \\ $$$$\int{x}\mathrm{sin}\:{x}\:\mathrm{then}\:\mathrm{g}=\mathrm{sin}\:{x}\:,\:\mathrm{f}={x}\:.\:\left(\mathrm{ILATE}\:\right) \\ $$$$\Rightarrow\:\int\mathrm{g}=\:−\mathrm{cos}\:{x}\:,\:\mathrm{f}'\:=\:\mathrm{1}. \\ $$$$\int\mathrm{fg}=\:\mathrm{f}\int\mathrm{g}\:−\:\int\mathrm{f}'\:\int\mathrm{g} \\ $$$$\:\Rightarrow\:{x}\left(−\mathrm{cos}\:{x}\right)\:−\:\int−\left(\mathrm{cos}\:{x}\right) \\ $$$$\Rightarrow\:−{x}\mathrm{cos}\:{x}+\mathrm{sin}\:{x}+{c}. \\ $$

Commented by MJS last updated on 02/Jun/18

we come from differentation: (uv)′=u′v+uv′ now integrate both sides: uv=∫u′v+∫uv′ that′s how I learned it...

$$\mathrm{we}\:\mathrm{come}\:\mathrm{from}\:\mathrm{differentation}: \\ $$$$\left({uv}\right)'={u}'{v}+{uv}' \\ $$$$\mathrm{now}\:\mathrm{integrate}\:\mathrm{both}\:\mathrm{sides}: \\ $$$${uv}=\int{u}'{v}+\int{uv}' \\ $$$$\mathrm{that}'\mathrm{s}\:\mathrm{how}\:\mathrm{I}\:\mathrm{learned}\:\mathrm{it}... \\ $$

Commented by rahul 19 last updated on 02/Jun/18

Is this also called integration by parts? Anyways,thanks!!

$$\mathrm{Is}\:\mathrm{this}\:\mathrm{also}\:\mathrm{called}\:\mathrm{integration}\:\mathrm{by}\:\mathrm{parts}? \\ $$$$\mathrm{Anyways},\mathrm{thanks}!! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com