
Question and Answers Forum
Question Number 36491 by rahul 19 last updated on 02/Jun/18

Answered by MJS last updated on 08/Jun/18
![just differentiate the following term: ±(1/((sec x +tan x)^((11)/2) ))((1/(11))±(1/7)(sec x +tan x)^2 ) write ∓ for changing signs. it′s faster than differentiating 4 terms, decide at the end which combination of signs is the right one. (d/dx)[±(1/((sec x +tan x)^((11)/2) ))((1/(11))±(1/7)(sec x +tan x)^2 )]= =±(d/dx)[((7±11(sec x+tan x)^2 )/(77(sec x+tan x)^((11)/2) ))]= [I write u for (sec x+tan x)] =±(d/dx)[((7±11u^2 )/(77u^((11)/2) ))]=±((±22uu′×77u^((11)/2) −(7±11u^2 )×((847)/2)u^(9/2) u′)/(5929u^(11) ))= =±((±1694u^((13)/2) −((5929)/2)u^(9/2) ∓((9317)/2)u^((13)/2) )/(5929u^(11) ))u′= =±((∓((5929)/2)u^((13)/2) −((5929)/2)u^(9/2) )/(5929u^(11) ))u′= =±((∓u^2 −1)/(2u^((13)/2) ))u′= [u′=sec x (sec x+tan x)=usec x] =±((∓u^2 −1)/(2u^((11)/2) ))sec x=(((sec x+tan x)^2 ∓1)/(2(sec x+tan x)^((11)/3) ))sec x](Q36511.png)
Commented by rahul 19 last updated on 03/Jun/18

Answered by tanmay.chaudhury50@gmail.com last updated on 03/Jun/18
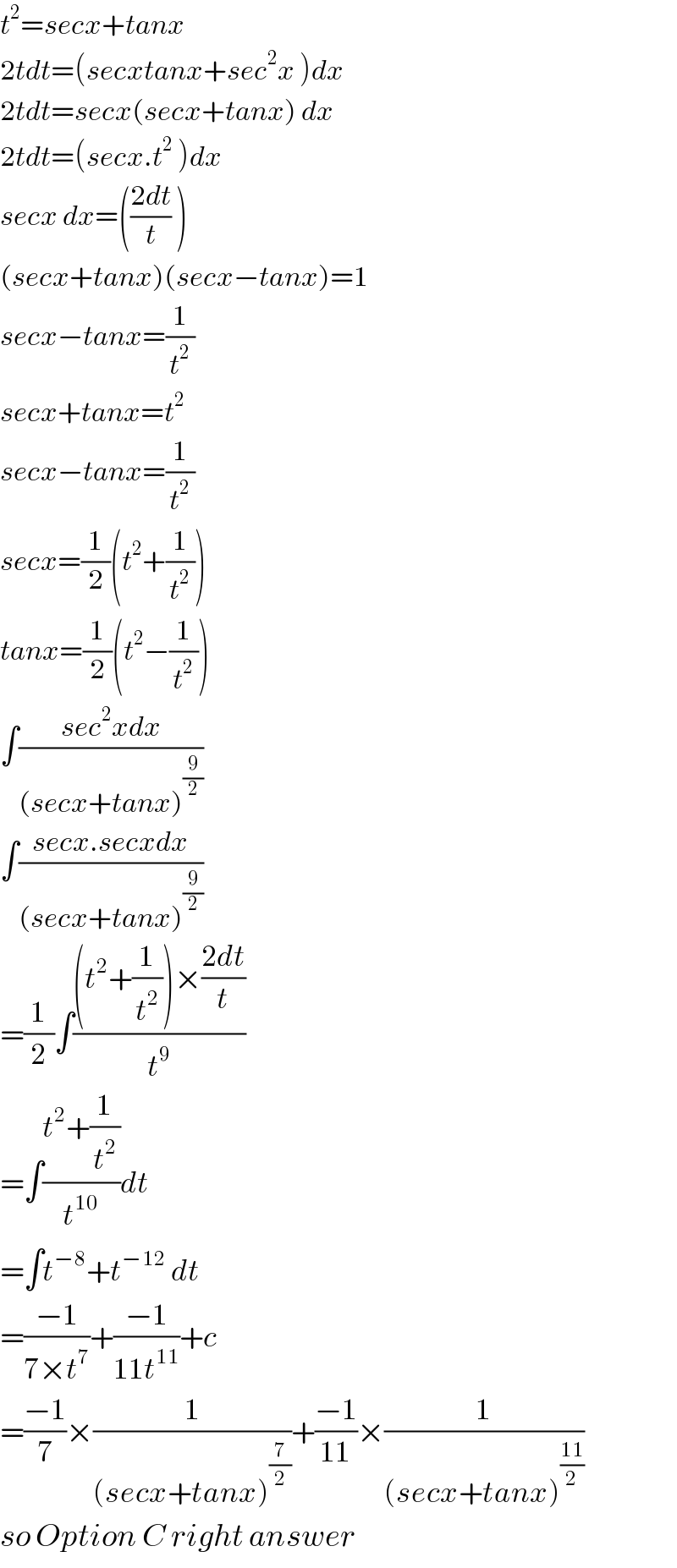
| ||
Question and Answers Forum | ||
Question Number 36491 by rahul 19 last updated on 02/Jun/18 | ||
 | ||
Answered by MJS last updated on 08/Jun/18 | ||
![just differentiate the following term: ±(1/((sec x +tan x)^((11)/2) ))((1/(11))±(1/7)(sec x +tan x)^2 ) write ∓ for changing signs. it′s faster than differentiating 4 terms, decide at the end which combination of signs is the right one. (d/dx)[±(1/((sec x +tan x)^((11)/2) ))((1/(11))±(1/7)(sec x +tan x)^2 )]= =±(d/dx)[((7±11(sec x+tan x)^2 )/(77(sec x+tan x)^((11)/2) ))]= [I write u for (sec x+tan x)] =±(d/dx)[((7±11u^2 )/(77u^((11)/2) ))]=±((±22uu′×77u^((11)/2) −(7±11u^2 )×((847)/2)u^(9/2) u′)/(5929u^(11) ))= =±((±1694u^((13)/2) −((5929)/2)u^(9/2) ∓((9317)/2)u^((13)/2) )/(5929u^(11) ))u′= =±((∓((5929)/2)u^((13)/2) −((5929)/2)u^(9/2) )/(5929u^(11) ))u′= =±((∓u^2 −1)/(2u^((13)/2) ))u′= [u′=sec x (sec x+tan x)=usec x] =±((∓u^2 −1)/(2u^((11)/2) ))sec x=(((sec x+tan x)^2 ∓1)/(2(sec x+tan x)^((11)/3) ))sec x](Q36511.png) | ||
| ||
Commented by rahul 19 last updated on 03/Jun/18 | ||
 | ||
Answered by tanmay.chaudhury50@gmail.com last updated on 03/Jun/18 | ||
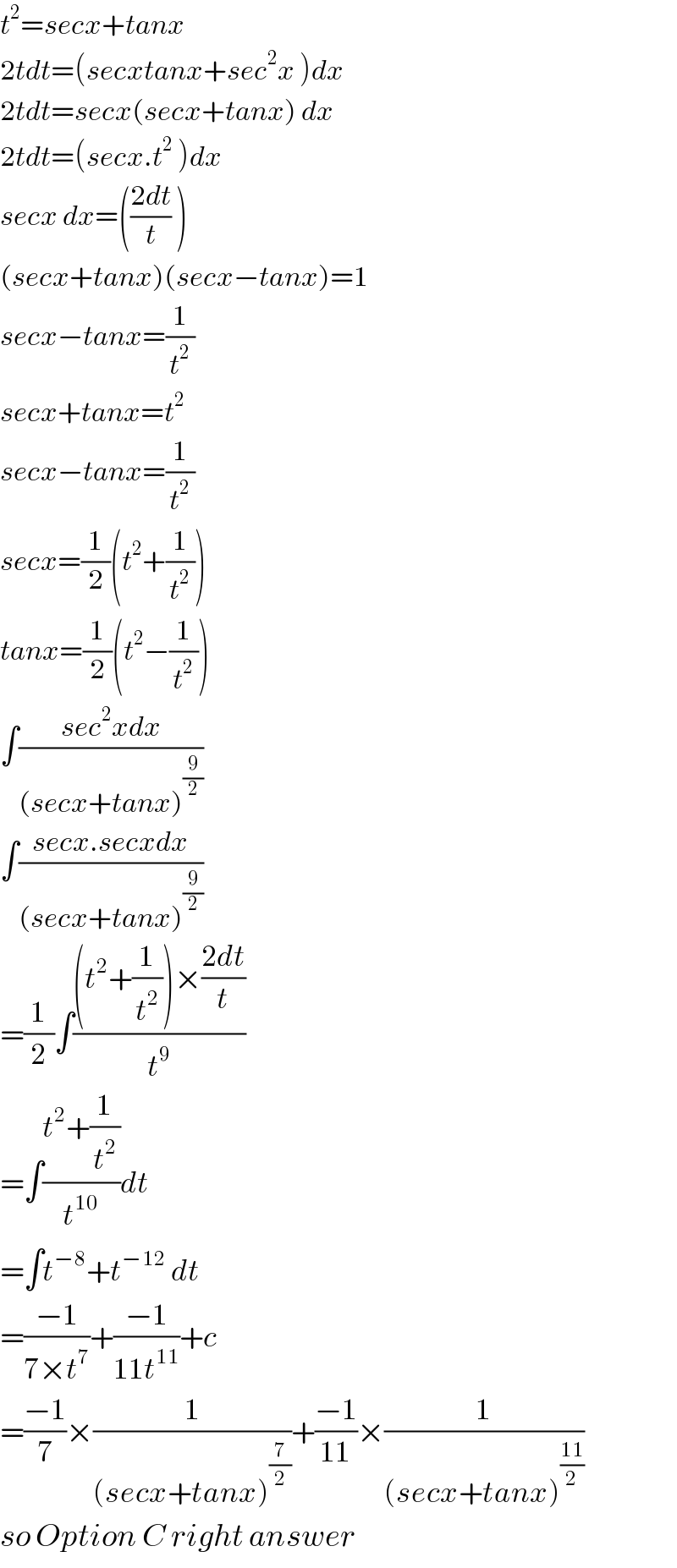 | ||
| ||