
Question and Answers Forum
Question Number 3650 by prakash jain last updated on 18/Dec/15

Answered by Yozzii last updated on 18/Dec/15

Commented byprakash jain last updated on 18/Dec/15
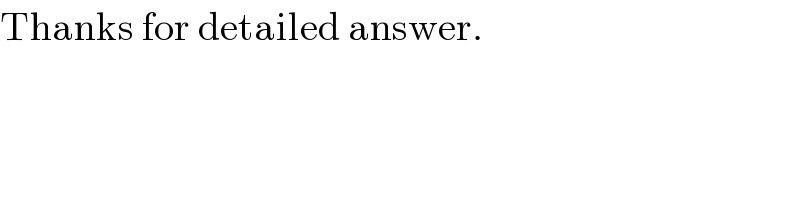
Commented byYozzii last updated on 18/Dec/15
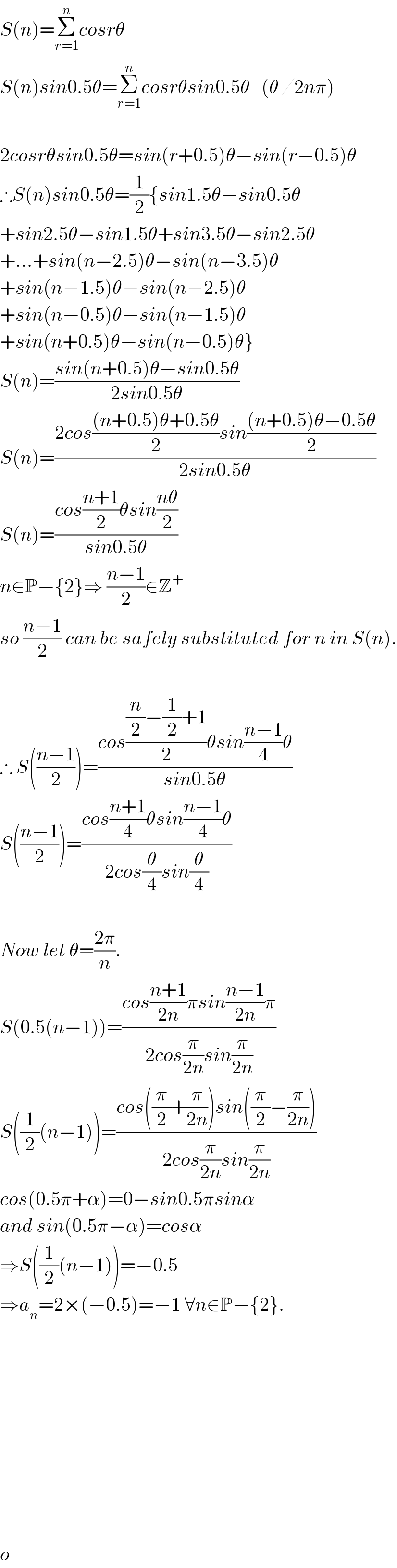
Commented byprakash jain last updated on 18/Dec/15

Commented byYozzii last updated on 18/Dec/15

