Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 36547 by tanmay.chaudhury50@gmail.com last updated on 03/Jun/18

∫((5x^4 +4x^5 )/((x^5 +x+1)^2 ))

$$\int\frac{\mathrm{5}{x}^{\mathrm{4}} +\mathrm{4}{x}^{\mathrm{5}} }{\left({x}^{\mathrm{5}} +{x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$

Answered by ajfour last updated on 03/Jun/18

=−∫(((−(5/x^6 )−(4/x^5 ))dx)/((1+(1/x^4 )+(1/x^5 ))^2 ))=−∫(dt/t^2 ) =(1/t)+c = (x^5 /(x^5 +x+1))+c .

$$=−\int\frac{\left(−\frac{\mathrm{5}}{{x}^{\mathrm{6}} }−\frac{\mathrm{4}}{{x}^{\mathrm{5}} }\right){dx}}{\left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{4}} }+\frac{\mathrm{1}}{{x}^{\mathrm{5}} }\right)^{\mathrm{2}} }=−\int\frac{{dt}}{{t}^{\mathrm{2}} } \\ $$$$\:=\frac{\mathrm{1}}{{t}}+{c}\:\:=\:\frac{{x}^{\mathrm{5}} }{{x}^{\mathrm{5}} +{x}+\mathrm{1}}+{c}\:. \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 03/Jun/18

bah...very good...excellent...

$${bah}...{very}\:{good}...{excellent}... \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 03/Jun/18

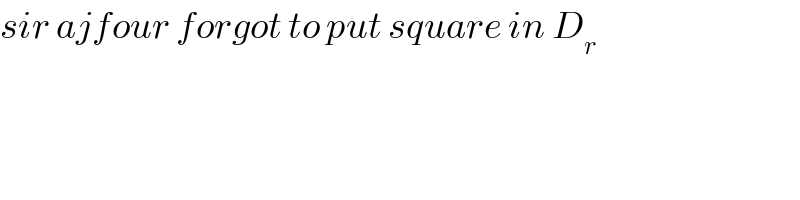
sir ajfour forgot to put square in D_r

$${sir}\:{ajfour}\:{forgot}\:{to}\:{put}\:{square}\:{in}\:{D}_{{r}} \\ $$

Commented by ajfour last updated on 03/Jun/18

yes, very silly !

$${yes},\:{very}\:{silly}\:! \\ $$

Answered by MJS last updated on 03/Jun/18

Ostrogradski′s Method once more ∫((p(x))/(q(x)))dx=((p_1 (x))/(q_1 (x)))+∫((p_2 (x))/(q_2 (x)))dx q_1 (x)=gcd(q(x), q′(x)) q_2 (x)=((q(x))/(q_1 (x))) p_1 , p_2 (polynomes, degree(p_i )<degree(q_i )) we get like this: (∫((p(x))/(q(x)))dx=((p_1 (x))/(q_1 (x)))+∫((p_2 (x))/(q_2 (x)))dx)′ ⇒ ⇒ ((p(x))/(q(x)))=(((p_1 (x))/(q_1 (x))))′+((p_2 (x))/(q_2 (x))) match the constants in this case p(x)=4x^5 +5x^4 q(x)=(x^5 +x+1)^2 q′(x)=2(5x^4 +1)(x^5 +x+1) q_1 (x)=q_2 (x)=x^5 +x+1 ((4x^5 +5x^4 )/((x^5 +x+1)^2 ))=(((c_1 x^4 +c_2 x^3 +c_3 x^2 +c_4 x+c_5 )/(x^5 +x+1)))′+((c_6 x^4 +c_7 x^3 +c_8 x^2 +c_9 x+c_(10) )/(x^5 +x+1)) ⇒ ⇒ c_4 =−1; c_5 =−1; all other c_i =0 p_1 (x)=−x−1 p_2 (x)=0 ∫((5x^4 +4x^5 )/((x^5 +x+1)^2 ))=−((x+1)/(x^5 +x+1))+C

$$\mathrm{Ostrogradski}'\mathrm{s}\:\mathrm{Method}\:\mathrm{once}\:\mathrm{more} \\ $$$$\int\frac{{p}\left({x}\right)}{{q}\left({x}\right)}{dx}=\frac{{p}_{\mathrm{1}} \left({x}\right)}{{q}_{\mathrm{1}} \left({x}\right)}+\int\frac{{p}_{\mathrm{2}} \left({x}\right)}{{q}_{\mathrm{2}} \left({x}\right)}{dx} \\ $$$${q}_{\mathrm{1}} \left({x}\right)=\mathrm{gcd}\left({q}\left({x}\right),\:{q}'\left({x}\right)\right) \\ $$$${q}_{\mathrm{2}} \left({x}\right)=\frac{{q}\left({x}\right)}{{q}_{\mathrm{1}} \left({x}\right)} \\ $$$${p}_{\mathrm{1}} ,\:{p}_{\mathrm{2}} \:\left(\mathrm{polynomes},\:\mathrm{degree}\left({p}_{{i}} \right)<\mathrm{degree}\left({q}_{{i}} \right)\right) \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{like}\:\mathrm{this}: \\ $$$$\left(\int\frac{{p}\left({x}\right)}{{q}\left({x}\right)}{dx}=\frac{{p}_{\mathrm{1}} \left({x}\right)}{{q}_{\mathrm{1}} \left({x}\right)}+\int\frac{{p}_{\mathrm{2}} \left({x}\right)}{{q}_{\mathrm{2}} \left({x}\right)}{dx}\right)'\:\Rightarrow \\ $$$$\Rightarrow\:\frac{{p}\left({x}\right)}{{q}\left({x}\right)}=\left(\frac{{p}_{\mathrm{1}} \left({x}\right)}{{q}_{\mathrm{1}} \left({x}\right)}\right)'+\frac{{p}_{\mathrm{2}} \left({x}\right)}{{q}_{\mathrm{2}} \left({x}\right)} \\ $$$$\mathrm{match}\:\mathrm{the}\:\mathrm{constants} \\ $$$$ \\ $$$$\mathrm{in}\:\mathrm{this}\:\mathrm{case} \\ $$$${p}\left({x}\right)=\mathrm{4}{x}^{\mathrm{5}} +\mathrm{5}{x}^{\mathrm{4}} \\ $$$${q}\left({x}\right)=\left({x}^{\mathrm{5}} +{x}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$${q}'\left({x}\right)=\mathrm{2}\left(\mathrm{5}{x}^{\mathrm{4}} +\mathrm{1}\right)\left({x}^{\mathrm{5}} +{x}+\mathrm{1}\right) \\ $$$${q}_{\mathrm{1}} \left({x}\right)={q}_{\mathrm{2}} \left({x}\right)={x}^{\mathrm{5}} +{x}+\mathrm{1} \\ $$$$\frac{\mathrm{4}{x}^{\mathrm{5}} +\mathrm{5}{x}^{\mathrm{4}} }{\left({x}^{\mathrm{5}} +{x}+\mathrm{1}\right)^{\mathrm{2}} }=\left(\frac{{c}_{\mathrm{1}} {x}^{\mathrm{4}} +{c}_{\mathrm{2}} {x}^{\mathrm{3}} +{c}_{\mathrm{3}} {x}^{\mathrm{2}} +{c}_{\mathrm{4}} {x}+{c}_{\mathrm{5}} }{{x}^{\mathrm{5}} +{x}+\mathrm{1}}\right)'+\frac{{c}_{\mathrm{6}} {x}^{\mathrm{4}} +{c}_{\mathrm{7}} {x}^{\mathrm{3}} +{c}_{\mathrm{8}} {x}^{\mathrm{2}} +{c}_{\mathrm{9}} {x}+{c}_{\mathrm{10}} }{{x}^{\mathrm{5}} +{x}+\mathrm{1}}\:\Rightarrow \\ $$$$\Rightarrow\:{c}_{\mathrm{4}} =−\mathrm{1};\:{c}_{\mathrm{5}} =−\mathrm{1};\:\mathrm{all}\:\mathrm{other}\:{c}_{{i}} =\mathrm{0} \\ $$$${p}_{\mathrm{1}} \left({x}\right)=−{x}−\mathrm{1} \\ $$$${p}_{\mathrm{2}} \left({x}\right)=\mathrm{0} \\ $$$$ \\ $$$$\int\frac{\mathrm{5}{x}^{\mathrm{4}} +\mathrm{4}{x}^{\mathrm{5}} }{\left({x}^{\mathrm{5}} +{x}+\mathrm{1}\right)^{\mathrm{2}} }=−\frac{{x}+\mathrm{1}}{{x}^{\mathrm{5}} +{x}+\mathrm{1}}+{C} \\ $$

Commented by MJS last updated on 03/Jun/18

...I didn′t see it either...

$$...\mathrm{I}\:\mathrm{didn}'\mathrm{t}\:\mathrm{see}\:\mathrm{it}\:\mathrm{either}... \\ $$

Commented by ajfour last updated on 03/Jun/18

please check.

$${please}\:{check}. \\ $$

Commented by MJS last updated on 03/Jun/18

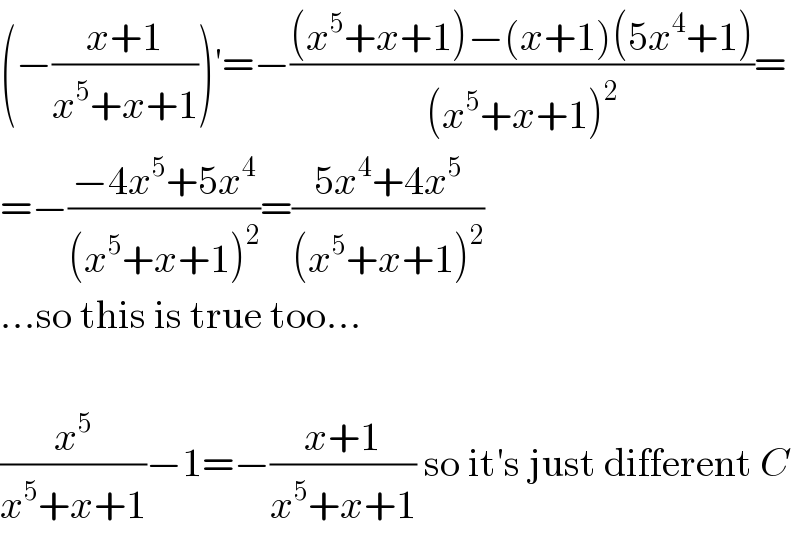
(−((x+1)/(x^5 +x+1)))′=−(((x^5 +x+1)−(x+1)(5x^4 +1))/((x^5 +x+1)^2 ))= =−((−4x^5 +5x^4 )/((x^5 +x+1)^2 ))=((5x^4 +4x^5 )/((x^5 +x+1)^2 )) ...so this is true too... (x^5 /(x^5 +x+1))−1=−((x+1)/(x^5 +x+1)) so it′s just different C

$$\left(−\frac{{x}+\mathrm{1}}{{x}^{\mathrm{5}} +{x}+\mathrm{1}}\right)'=−\frac{\left({x}^{\mathrm{5}} +{x}+\mathrm{1}\right)−\left({x}+\mathrm{1}\right)\left(\mathrm{5}{x}^{\mathrm{4}} +\mathrm{1}\right)}{\left({x}^{\mathrm{5}} +{x}+\mathrm{1}\right)^{\mathrm{2}} }= \\ $$$$=−\frac{−\mathrm{4}{x}^{\mathrm{5}} +\mathrm{5}{x}^{\mathrm{4}} }{\left({x}^{\mathrm{5}} +{x}+\mathrm{1}\right)^{\mathrm{2}} }=\frac{\mathrm{5}{x}^{\mathrm{4}} +\mathrm{4}{x}^{\mathrm{5}} }{\left({x}^{\mathrm{5}} +{x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$...\mathrm{so}\:\mathrm{this}\:\mathrm{is}\:\mathrm{true}\:\mathrm{too}... \\ $$$$ \\ $$$$\frac{{x}^{\mathrm{5}} }{{x}^{\mathrm{5}} +{x}+\mathrm{1}}−\mathrm{1}=−\frac{{x}+\mathrm{1}}{{x}^{\mathrm{5}} +{x}+\mathrm{1}}\:\mathrm{so}\:\mathrm{it}'\mathrm{s}\:\mathrm{just}\:\mathrm{different}\:{C} \\ $$

Commented by ajfour last updated on 03/Jun/18

o′ yes! thanks.

$${o}'\:{yes}!\:{thanks}. \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 03/Jun/18

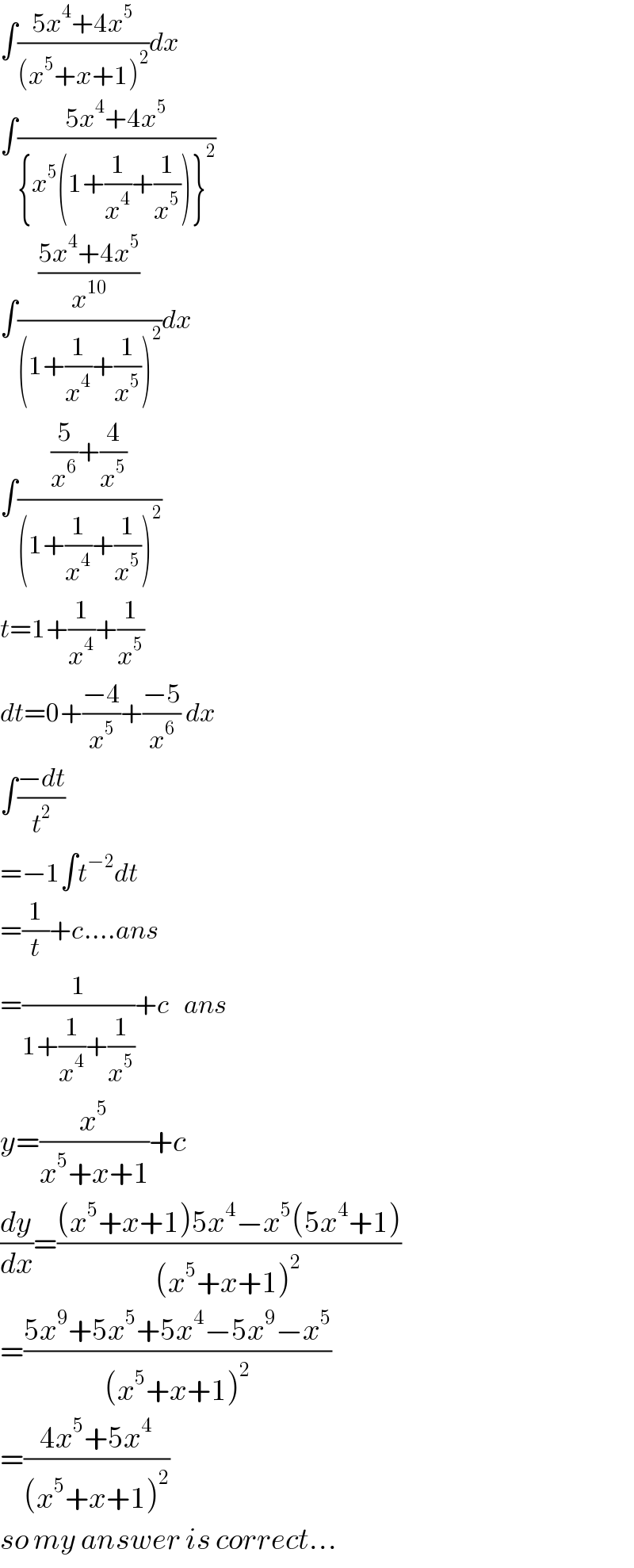
∫((5x^4 +4x^5 )/((x^5 +x+1)^2 ))dx ∫((5x^4 +4x^5 )/({x^5 (1+(1/x^4 )+(1/x^5 ))}^2 )) ∫(((5x^4 +4x^5 )/x^(10) )/((1+(1/x^4 )+(1/x^5 ))^2 ))dx ∫(((5/x^6 )+(4/x^5 ))/((1+(1/x^4 )+(1/x^5 ))^2 )) t=1+(1/x^4 )+(1/x^5 ) dt=0+((−4)/x^5 )+((−5)/x^6 ) dx ∫((−dt)/t^2 ) =−1∫t^(−2) dt =(1/t)+c....ans =(1/(1+(1/x^4 )+(1/x^5 )))+c ans y=(x^5 /(x^5 +x+1))+c (dy/dx)=(((x^5 +x+1)5x^4 −x^5 (5x^4 +1))/((x^5 +x+1)^2 )) =((5x^9 +5x^5 +5x^4 −5x^9 −x^5 )/((x^5 +x+1)^2 )) =((4x^5 +5x^4 )/((x^5 +x+1)^2 )) so my answer is correct...

$$\int\frac{\mathrm{5}{x}^{\mathrm{4}} +\mathrm{4}{x}^{\mathrm{5}} }{\left({x}^{\mathrm{5}} +{x}+\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$$$\int\frac{\mathrm{5}{x}^{\mathrm{4}} +\mathrm{4}{x}^{\mathrm{5}} }{\left\{{x}^{\mathrm{5}} \left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{4}} }+\frac{\mathrm{1}}{{x}^{\mathrm{5}} }\right)\right\}^{\mathrm{2}} } \\ $$$$\int\frac{\frac{\mathrm{5}{x}^{\mathrm{4}} +\mathrm{4}{x}^{\mathrm{5}} }{{x}^{\mathrm{10}} }}{\left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{4}} }+\frac{\mathrm{1}}{{x}^{\mathrm{5}} }\right)^{\mathrm{2}} }{dx} \\ $$$$\int\frac{\frac{\mathrm{5}}{{x}^{\mathrm{6}} }+\frac{\mathrm{4}}{{x}^{\mathrm{5}} }}{\left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{4}} }+\frac{\mathrm{1}}{{x}^{\mathrm{5}} }\right)^{\mathrm{2}} } \\ $$$${t}=\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{4}} }+\frac{\mathrm{1}}{{x}^{\mathrm{5}} } \\ $$$${dt}=\mathrm{0}+\frac{−\mathrm{4}}{{x}^{\mathrm{5}} }+\frac{−\mathrm{5}}{{x}^{\mathrm{6}} }\:{dx} \\ $$$$\int\frac{−{dt}}{{t}^{\mathrm{2}} } \\ $$$$=−\mathrm{1}\int{t}^{−\mathrm{2}} {dt} \\ $$$$=\frac{\mathrm{1}}{{t}}+{c}....{ans} \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{4}} }+\frac{\mathrm{1}}{{x}^{\mathrm{5}} }}+{c}\:\:\:{ans} \\ $$$${y}=\frac{{x}^{\mathrm{5}} }{{x}^{\mathrm{5}} +{x}+\mathrm{1}}+{c} \\ $$$$\frac{{dy}}{{dx}}=\frac{\left({x}^{\mathrm{5}} +{x}+\mathrm{1}\right)\mathrm{5}{x}^{\mathrm{4}} −{x}^{\mathrm{5}} \left(\mathrm{5}{x}^{\mathrm{4}} +\mathrm{1}\right)}{\left({x}^{\mathrm{5}} +{x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{5}{x}^{\mathrm{9}} +\mathrm{5}{x}^{\mathrm{5}} +\mathrm{5}{x}^{\mathrm{4}} −\mathrm{5}{x}^{\mathrm{9}} −{x}^{\mathrm{5}} }{\left({x}^{\mathrm{5}} +{x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{4}{x}^{\mathrm{5}} +\mathrm{5}{x}^{\mathrm{4}} }{\left({x}^{\mathrm{5}} +{x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${so}\:{my}\:{answer}\:{is}\:{correct}... \\ $$

Commented by ajfour last updated on 03/Jun/18

thanks, i′ve corrected.

$${thanks},\:{i}'{ve}\:{corrected}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com