
Question and Answers Forum
Question Number 36563 by bshahid010@gmail.com last updated on 03/Jun/18

Commented by prof Abdo imad last updated on 03/Jun/18
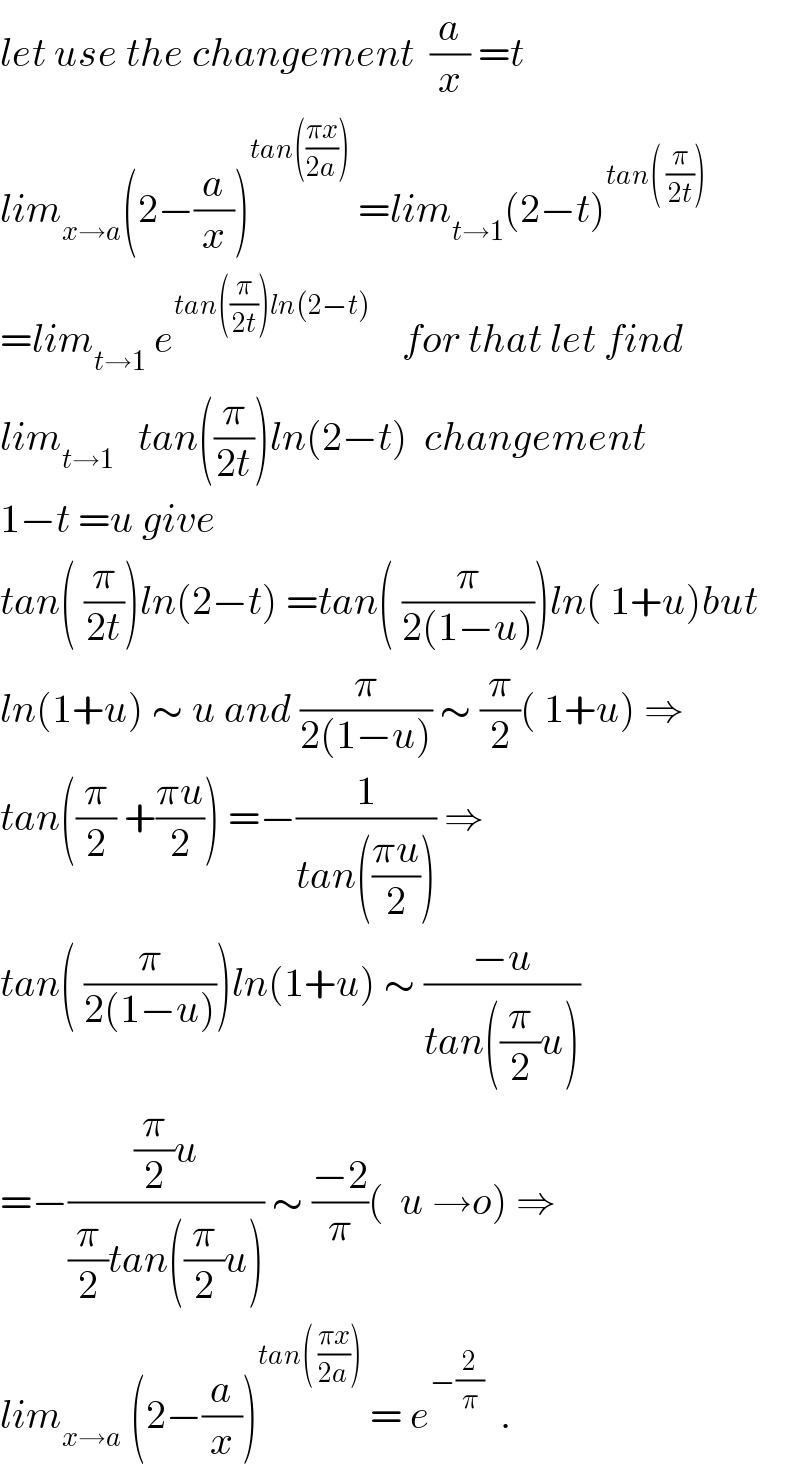
Answered by ajfour last updated on 03/Jun/18
![L=lim_(x→a) {[1+(1−(a/x))]^(1/(1−(a/x))) }^((1−(a/x))/(tan ((π/2)(1−(x/a))))) ⇒ L = e^(2/π) .](Q36565.png)
| ||
Question and Answers Forum | ||
Question Number 36563 by bshahid010@gmail.com last updated on 03/Jun/18 | ||
 | ||
Commented by prof Abdo imad last updated on 03/Jun/18 | ||
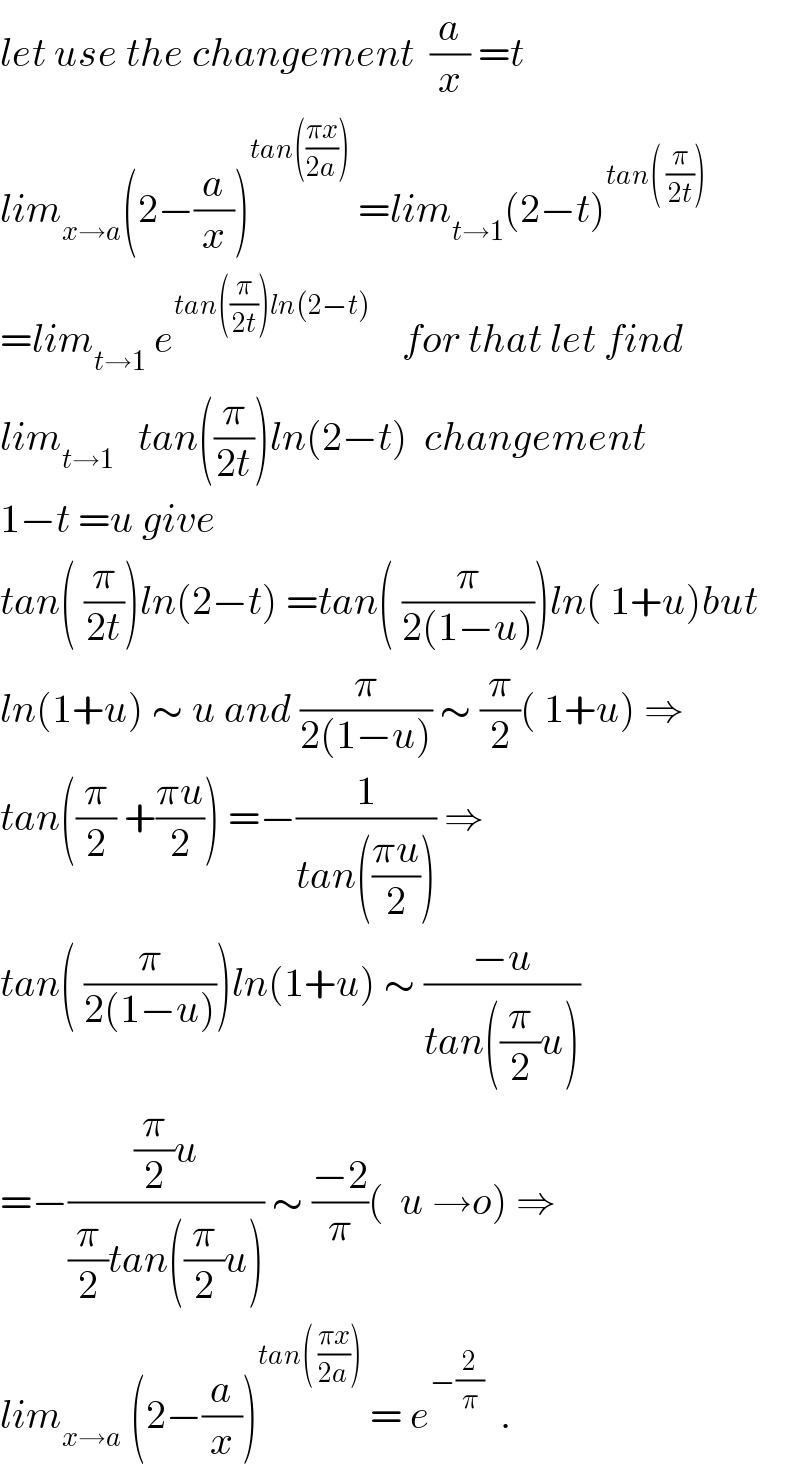 | ||
Answered by ajfour last updated on 03/Jun/18 | ||
![L=lim_(x→a) {[1+(1−(a/x))]^(1/(1−(a/x))) }^((1−(a/x))/(tan ((π/2)(1−(x/a))))) ⇒ L = e^(2/π) .](Q36565.png) | ||
| ||