
Question and Answers Forum
Question Number 36677 by mondodotto@gmail.com last updated on 04/Jun/18
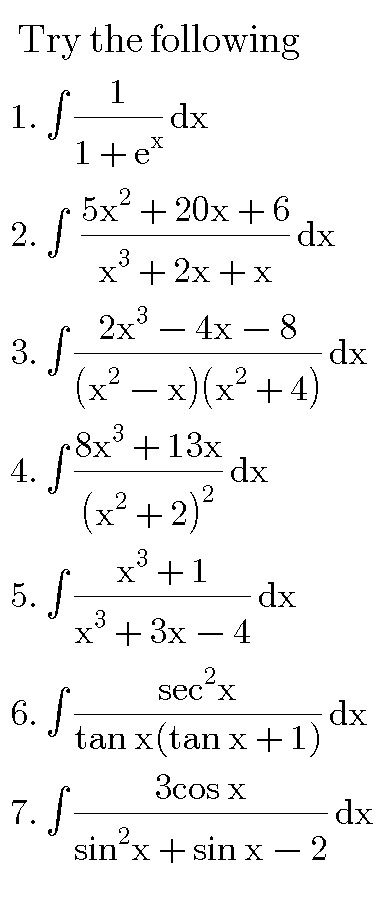
Commented by prof Abdo imad last updated on 04/Jun/18
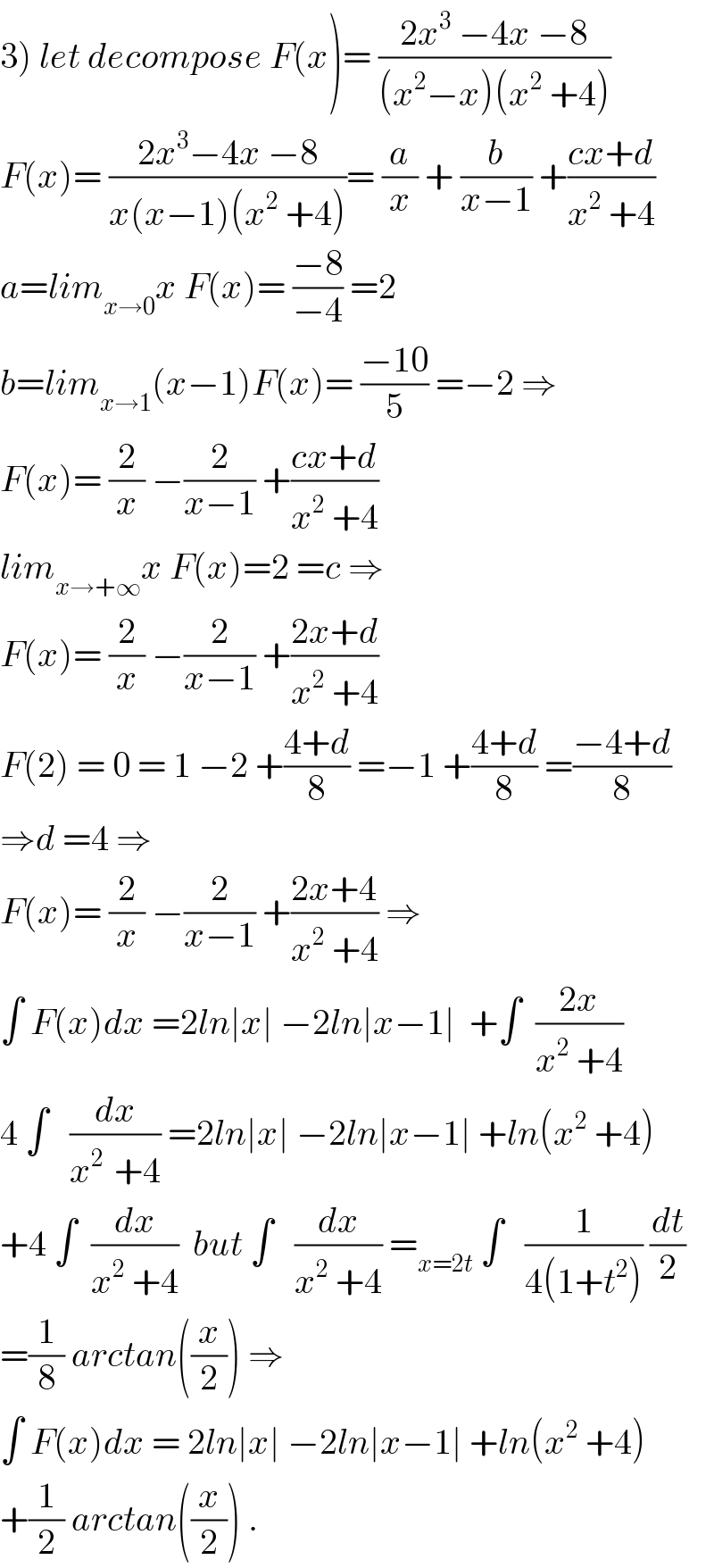
Commented by abdo mathsup last updated on 04/Jun/18
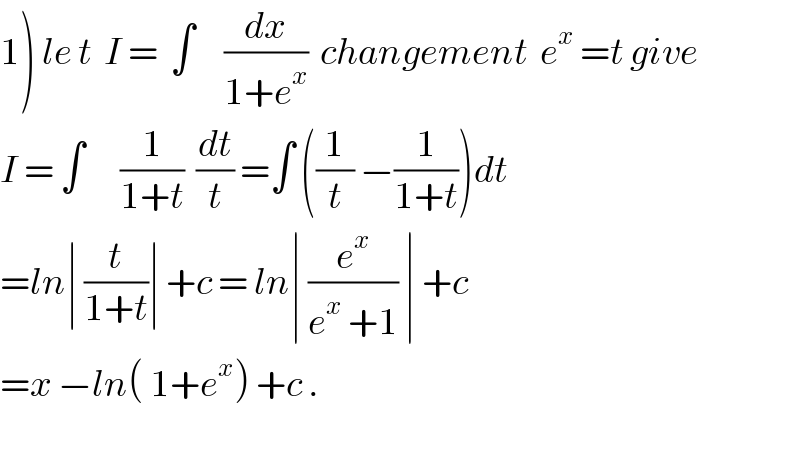
Commented by Cheyboy last updated on 04/Jun/18
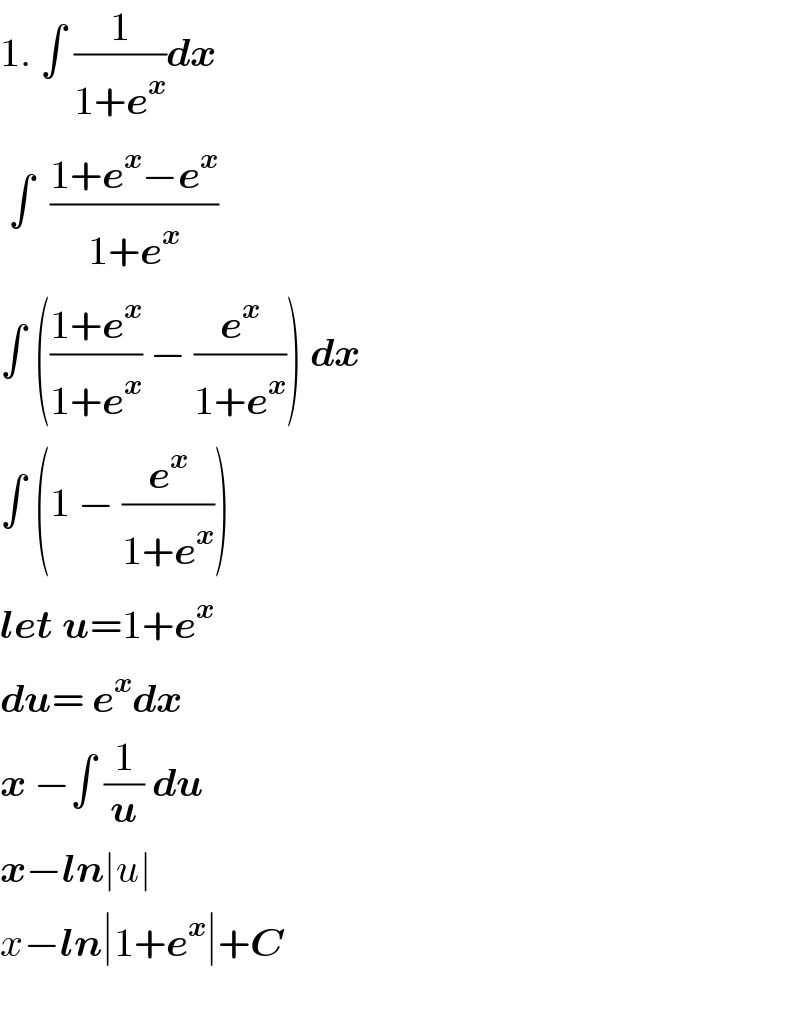
Answered by tanmay.chaudhury50@gmail.com last updated on 04/Jun/18
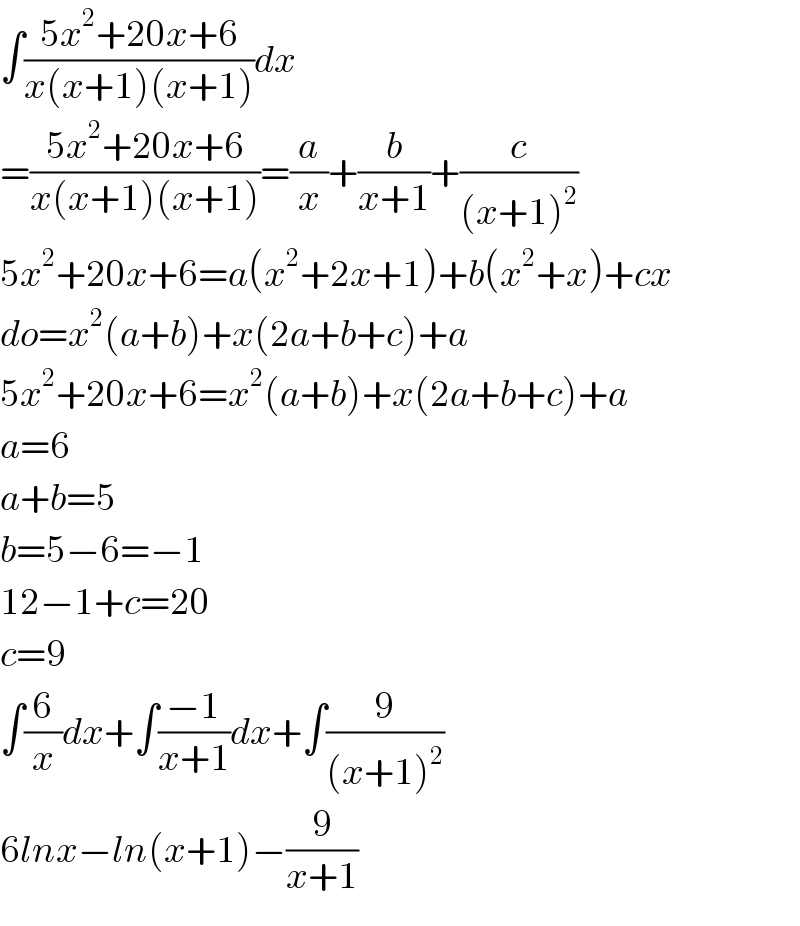
Answered by tanmay.chaudhury50@gmail.com last updated on 04/Jun/18
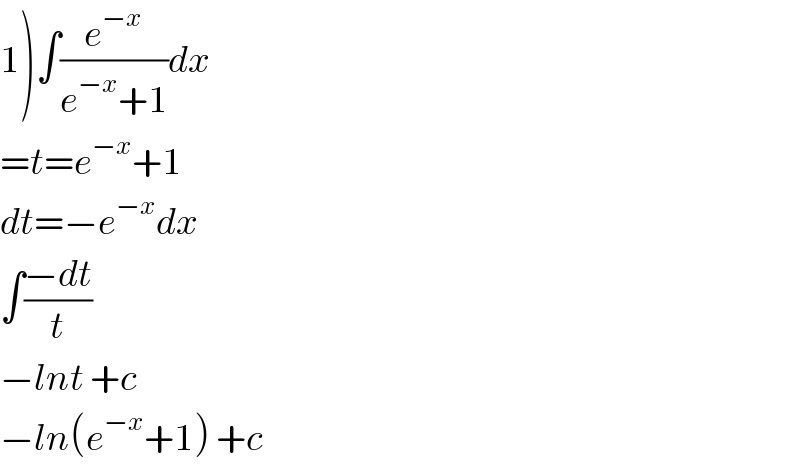
Answered by tanmay.chaudhury50@gmail.com last updated on 04/Jun/18
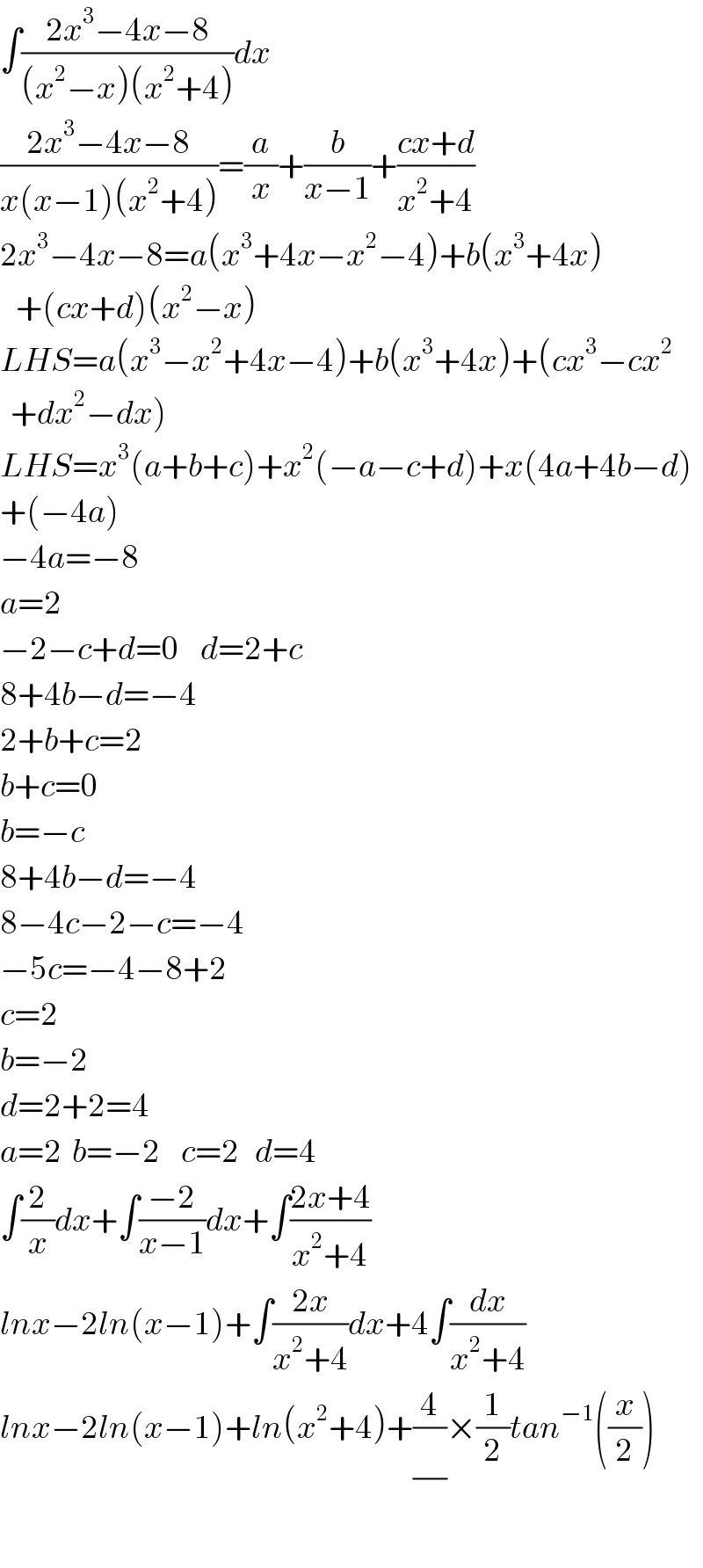
Answered by MJS last updated on 04/Jun/18
![6. ∫((sec^2 x)/(tan x (tan x +1)))dx= [t=tan x → dx=(dt/(sec^2 x))] =∫(dt/(t(t+1)))=∫(A/t)dt+∫(B/(t+1))dt= =∫(dt/t)−∫(dt/(t+1))=ln t −ln(t+1)= =ln∣tan x∣−ln∣tan x +1∣+C 7. ∫((3cos x)/(sin^2 x +sin x −2))dx= [t=sin x → dx=(dt/(cos x))] =∫(3/(t^2 +t−2))dt=∫(3/((t−1)(t+2)))dt= =∫(dt/(t−1))−∫(dt/(t+2))=ln(t−1)−ln(t+2)= [∣sin x −1∣=1−sin x] =ln(1−sin x)−ln(2+sin x)+C](Q36705.png)
