
Question and Answers Forum
Question Number 36690 by prof Abdo imad last updated on 04/Jun/18
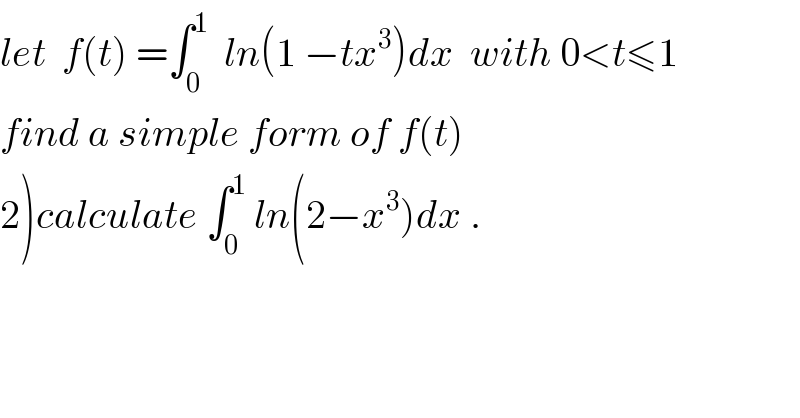
Commented bymaxmathsup by imad last updated on 03/Aug/18
![we have f^′ (t) =−∫_0 ^1 (x^3 /(1−tx^3 ))dx =−∫_0 ^1 x^3 (Σ_(n=0) ^∞ t^n x^(3n) dx =−Σ_(n=0) ^∞ t^n ∫_0 ^1 x^(3(n+1)) dx =−Σ_(n=0) ^∞ (t^n /(3n+4)) =−(1/((^3 (√t))^4 ))Σ_(n=0) ^∞ (((^3 (√t))^(3n +4) )/(3n+4)) =−(1/((^3 (√t))^4 )) ϕ(^3 (√t)) with ϕ(x) =Σ_(n=0) ^∞ (x^(3n+4) /(3n+4)) ⇒ϕ^′ (x)= Σ_(n=0) ^∞ x^(3n+3) =x^3 Σ_(n=0) ^∞ (x^3 )^n =x^3 (1/(1−x^3 )) =(x^3 /(1−x^3 )) ⇒ϕ(x) = ∫_0 ^x (t^3 /(1−t^3 )) dt +c withc=ϕ(0)=0 ⇒ ϕ(x)=−∫_0 ^x (t^3 /(t^3 −1))dt =−∫_0 ^x ((t^3 −1 +1)/(t^3 −1))dt =−x −∫_0 ^x (dt/(t^3 −1)) let decompose F(t) = (1/(t^3 −1)) F(t)= (1/((t−1)(t^2 +t+1))) =(a/(t−1)) +((bt+c)/(t^2 +t +1)) a =lim_(t→1) (t−1)F(t) =(1/3) lim_(t→+∞) tF(t) =0 =a +b ⇒b =−a ⇒ F(t) = (1/(3(t−1))) −(1/3) ((t −3c)/(t^2 +t+1)) F(0) =−1 =−(1/3) +c ⇒c=(1/3)−1 =−(2/3) ⇒F(t)=(1/(3(t−1))) −(1/3) ((t +2)/(t^2 +t+1)) ⇒ ∫ F(t)dt = (1/3)ln∣t−1∣ −(1/6) ∫ ((2t +1+3)/(t^2 +t +1))dt =(1/3)ln∣t−1∣ −(1/6)ln∣t^2 +t+1∣ −(1/2) ∫ (dt/((t+(1/2))^2 +(3/4))) but ∫ (dt/((t+(1/2))^2 +(3/4))) =_(t+(1/2)=((√3)/2)u) ∫ (1/((3/4)(1+u^2 ))) ((√3)/2) du=(4/3) ((√3)/2) arctan(((2t+1)/(√3))) =((2(√3))/3) arctan(((2t+1)/(√3))) ⇒ ϕ(x)=−x − [ (1/3)ln∣t−1∣−(1/6)ln(t^2 +t+1)−((√3)/3) arctan(((2t+1)/(√3)))]_0 ^x =−x −{(1/3)ln∣x−1∣−(1/6)ln(x^2 +x+1)−((√3)/3) arctan(((2x+1)/(√3)))+((√3)/3) arctan((1/(√3)))} we have f^′ (t)=−(1/((^3 (√t))^4 )) ϕ(^3 (√t)) so the value of f^′ (x) is known.. be continued...](Q41221.png)
| ||
Question and Answers Forum | ||
Question Number 36690 by prof Abdo imad last updated on 04/Jun/18 | ||
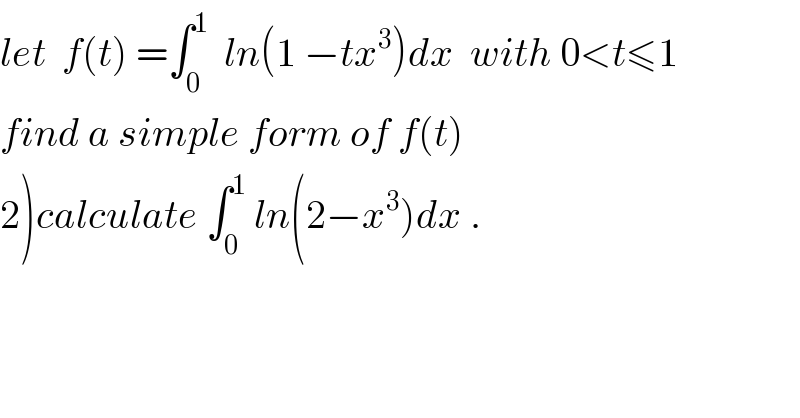 | ||
Commented bymaxmathsup by imad last updated on 03/Aug/18 | ||
![we have f^′ (t) =−∫_0 ^1 (x^3 /(1−tx^3 ))dx =−∫_0 ^1 x^3 (Σ_(n=0) ^∞ t^n x^(3n) dx =−Σ_(n=0) ^∞ t^n ∫_0 ^1 x^(3(n+1)) dx =−Σ_(n=0) ^∞ (t^n /(3n+4)) =−(1/((^3 (√t))^4 ))Σ_(n=0) ^∞ (((^3 (√t))^(3n +4) )/(3n+4)) =−(1/((^3 (√t))^4 )) ϕ(^3 (√t)) with ϕ(x) =Σ_(n=0) ^∞ (x^(3n+4) /(3n+4)) ⇒ϕ^′ (x)= Σ_(n=0) ^∞ x^(3n+3) =x^3 Σ_(n=0) ^∞ (x^3 )^n =x^3 (1/(1−x^3 )) =(x^3 /(1−x^3 )) ⇒ϕ(x) = ∫_0 ^x (t^3 /(1−t^3 )) dt +c withc=ϕ(0)=0 ⇒ ϕ(x)=−∫_0 ^x (t^3 /(t^3 −1))dt =−∫_0 ^x ((t^3 −1 +1)/(t^3 −1))dt =−x −∫_0 ^x (dt/(t^3 −1)) let decompose F(t) = (1/(t^3 −1)) F(t)= (1/((t−1)(t^2 +t+1))) =(a/(t−1)) +((bt+c)/(t^2 +t +1)) a =lim_(t→1) (t−1)F(t) =(1/3) lim_(t→+∞) tF(t) =0 =a +b ⇒b =−a ⇒ F(t) = (1/(3(t−1))) −(1/3) ((t −3c)/(t^2 +t+1)) F(0) =−1 =−(1/3) +c ⇒c=(1/3)−1 =−(2/3) ⇒F(t)=(1/(3(t−1))) −(1/3) ((t +2)/(t^2 +t+1)) ⇒ ∫ F(t)dt = (1/3)ln∣t−1∣ −(1/6) ∫ ((2t +1+3)/(t^2 +t +1))dt =(1/3)ln∣t−1∣ −(1/6)ln∣t^2 +t+1∣ −(1/2) ∫ (dt/((t+(1/2))^2 +(3/4))) but ∫ (dt/((t+(1/2))^2 +(3/4))) =_(t+(1/2)=((√3)/2)u) ∫ (1/((3/4)(1+u^2 ))) ((√3)/2) du=(4/3) ((√3)/2) arctan(((2t+1)/(√3))) =((2(√3))/3) arctan(((2t+1)/(√3))) ⇒ ϕ(x)=−x − [ (1/3)ln∣t−1∣−(1/6)ln(t^2 +t+1)−((√3)/3) arctan(((2t+1)/(√3)))]_0 ^x =−x −{(1/3)ln∣x−1∣−(1/6)ln(x^2 +x+1)−((√3)/3) arctan(((2x+1)/(√3)))+((√3)/3) arctan((1/(√3)))} we have f^′ (t)=−(1/((^3 (√t))^4 )) ϕ(^3 (√t)) so the value of f^′ (x) is known.. be continued...](Q41221.png) | ||