
Question and Answers Forum
Question Number 36728 by a1bgt3@gmail.com last updated on 04/Jun/18
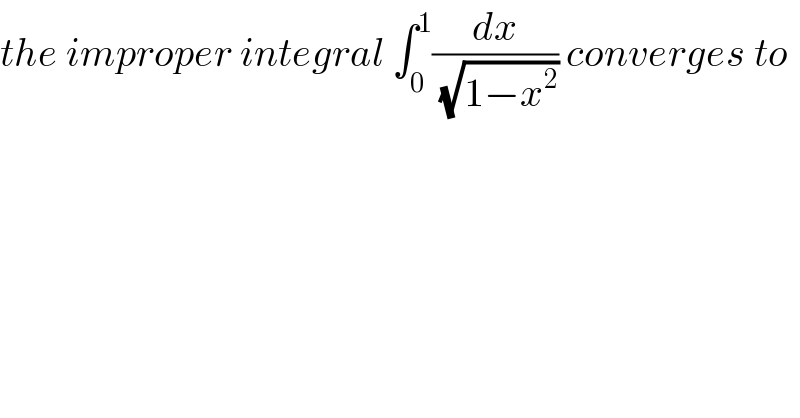
Commented by abdo.msup.com last updated on 05/Jun/18
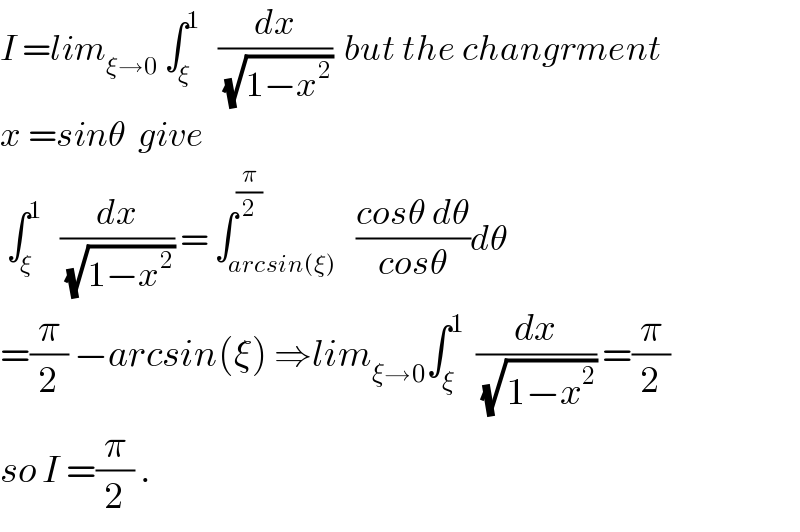
Answered by MJS last updated on 04/Jun/18
![∫_0 ^1 (dx/(√(1−x^2 )))=[arcsin x]_0 ^1 =(π/2) ...nothing improper about this...](Q36731.png)
| ||
Question and Answers Forum | ||
Question Number 36728 by a1bgt3@gmail.com last updated on 04/Jun/18 | ||
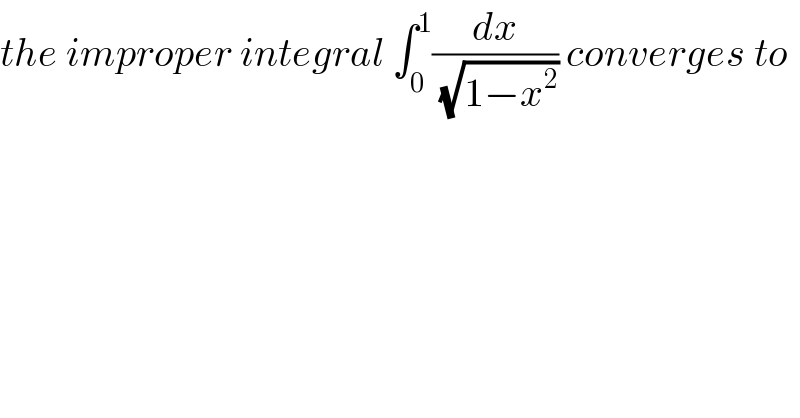 | ||
Commented by abdo.msup.com last updated on 05/Jun/18 | ||
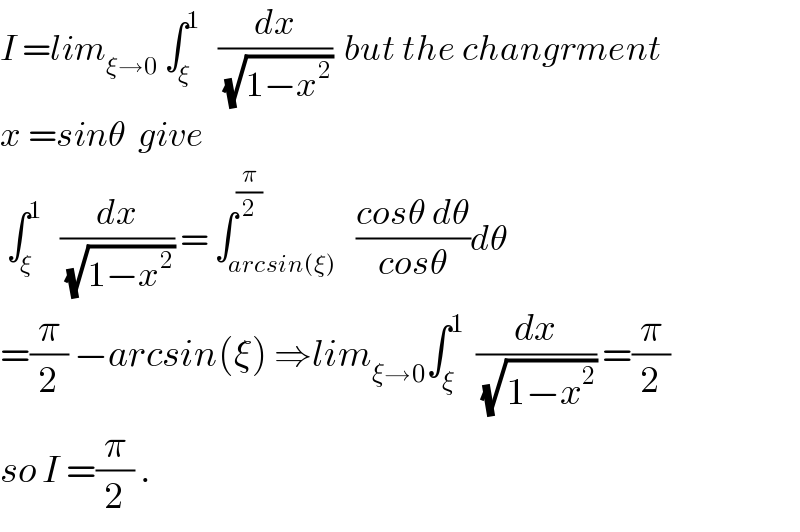 | ||
Answered by MJS last updated on 04/Jun/18 | ||
![∫_0 ^1 (dx/(√(1−x^2 )))=[arcsin x]_0 ^1 =(π/2) ...nothing improper about this...](Q36731.png) | ||
| ||