
Question and Answers Forum
Question Number 36799 by abdo.msup.com last updated on 05/Jun/18
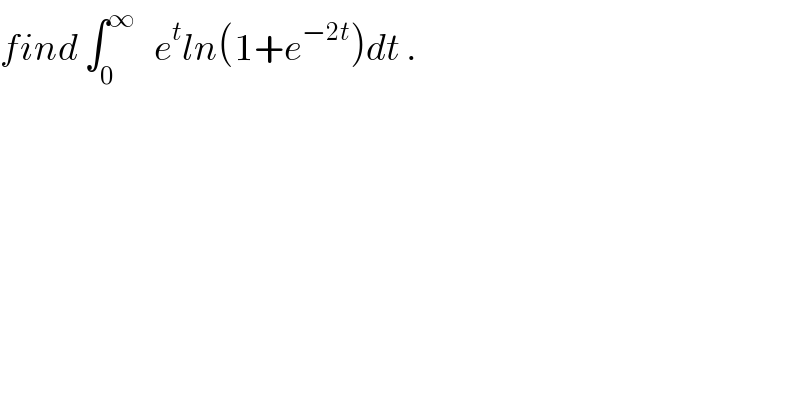
Commented by math khazana by abdo last updated on 11/Jun/18
![let I = ∫_0 ^∞ e^t ln(1+e^(−2t) )dt by parts u^′ =e^t and v =ln(1+e^(−2t) ) ⇒ I = [ e^t ln(1+e^(−2t) )]_0 ^(+∞) −∫_0 ^∞ e^t ((−2 e^(−2t) )/(1+e^(−2t) ))dt =−ln(2) +2 ∫_0 ^∞ (e^(−t) /(1+e^(−2t) )) dt but ∫_0 ^∞ (e^(−t) /(1+e^(−2t) )) dt =_(e^t =x) ∫_1 ^(+∞) (1/(x(1+(1/x^2 )))) (dx/x) = ∫_1 ^(+∞) (dx/(x^2 +1)) =[arctanx]_1 ^(+∞) =(π/2) −(π/4) =(π/4) ⇒ ★I = −ln(2) +(π/2) ★](Q37242.png)
Answered by MJS last updated on 06/Jun/18
![∫e^t ln(1+e^(−2t) )dt= [((∫f′g=fg−∫fg′)),((f′=e^t ⇒ f=e^t )),((g=ln(1+e^(−2t) ) ⇒ g′=−((2e^(−2t) )/(1+e^(−2t) )))) ] =e^t ln(1+e^(−2t) )−2∫−(e^(−t) /(1+e^(−2t) ))dt= [u=−e^t → dt=−e^t du] =e^t ln(1+e^(−2t) )−2∫(u/(1+u^2 ))du= =e^t ln(1+e^(−2t) )−2arctan u= =e^t ln(1+e^(−2t) )−2arctan −e^t = =e^t ln(1+e^(−2t) )+2arctan e^t +C ∫_0 ^∞ e^t ln(1+e^(−2t) )dt=(π/2)−ln 2](Q36832.png)
| ||
Question and Answers Forum | ||
Question Number 36799 by abdo.msup.com last updated on 05/Jun/18 | ||
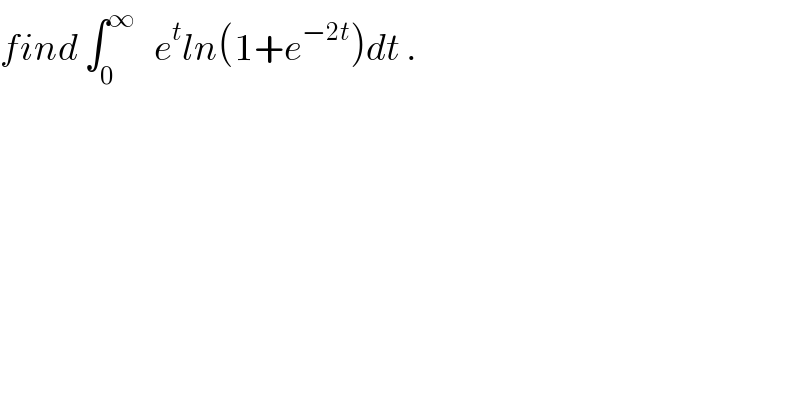 | ||
Commented by math khazana by abdo last updated on 11/Jun/18 | ||
![let I = ∫_0 ^∞ e^t ln(1+e^(−2t) )dt by parts u^′ =e^t and v =ln(1+e^(−2t) ) ⇒ I = [ e^t ln(1+e^(−2t) )]_0 ^(+∞) −∫_0 ^∞ e^t ((−2 e^(−2t) )/(1+e^(−2t) ))dt =−ln(2) +2 ∫_0 ^∞ (e^(−t) /(1+e^(−2t) )) dt but ∫_0 ^∞ (e^(−t) /(1+e^(−2t) )) dt =_(e^t =x) ∫_1 ^(+∞) (1/(x(1+(1/x^2 )))) (dx/x) = ∫_1 ^(+∞) (dx/(x^2 +1)) =[arctanx]_1 ^(+∞) =(π/2) −(π/4) =(π/4) ⇒ ★I = −ln(2) +(π/2) ★](Q37242.png) | ||
Answered by MJS last updated on 06/Jun/18 | ||
![∫e^t ln(1+e^(−2t) )dt= [((∫f′g=fg−∫fg′)),((f′=e^t ⇒ f=e^t )),((g=ln(1+e^(−2t) ) ⇒ g′=−((2e^(−2t) )/(1+e^(−2t) )))) ] =e^t ln(1+e^(−2t) )−2∫−(e^(−t) /(1+e^(−2t) ))dt= [u=−e^t → dt=−e^t du] =e^t ln(1+e^(−2t) )−2∫(u/(1+u^2 ))du= =e^t ln(1+e^(−2t) )−2arctan u= =e^t ln(1+e^(−2t) )−2arctan −e^t = =e^t ln(1+e^(−2t) )+2arctan e^t +C ∫_0 ^∞ e^t ln(1+e^(−2t) )dt=(π/2)−ln 2](Q36832.png) | ||
| ||