
Question and Answers Forum
Question Number 36801 by rahul 19 last updated on 05/Jun/18
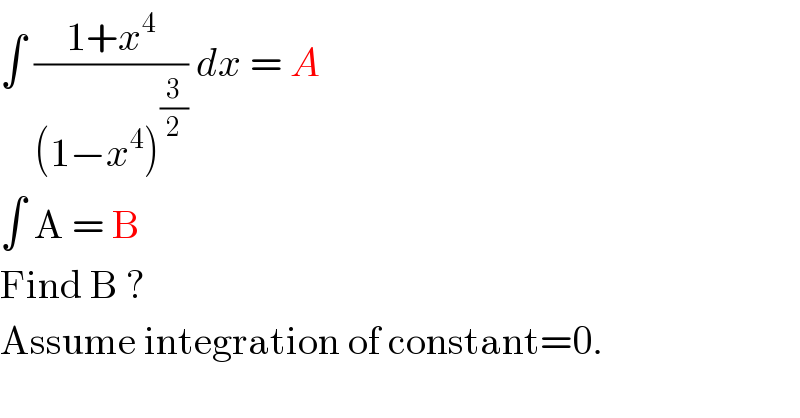
Answered by MJS last updated on 05/Jun/18
![A=(x/(√(1−x^4 ))) B=(1/2)arcsin x^2 A: ∫((1+x^4 )/((1−x^4 )^(3/2) ))dx looks like it′s ((p(x))/(√(1−x^4 ))) with p(x) is a polynome let′s try (d/dx)(((p(x))/(√(1−x^4 ))))=(d/dx)(p(x)(1−x^4 )^(−(1/2)) )= =p′(x)(1−x^4 )^(−(1/2)) +p(x)(2x^3 (1−x^4 )^(−(3/2)) )= =((p′(x)(1−x^4 )+2p(x)x^3 )/((1−x^4 )^(3/2) )) ⇒ p′(x)(1−x^4 )+2p(x)x^3 =1+x^4 let′s try p(x)=ax+b; p′(x)=a a+2bx^3 +ax^4 =1+x^4 a=1; b=0 p(x)=x ∫((1+x^4 )/((1−x^4 )^(3/2) ))dx=(x/(√(1−x^4 ))) B: ∫(x/(√(1−x^4 )))dx= [t=x^2 → dx=(dt/(2x))] =(1/2)∫(dt/(√(1−t^2 )))=(1/2)arcsin t= =(1/2)arcsin x^2](Q36810.png)
Answered by tanmay.chaudhury50@gmail.com last updated on 06/Jun/18
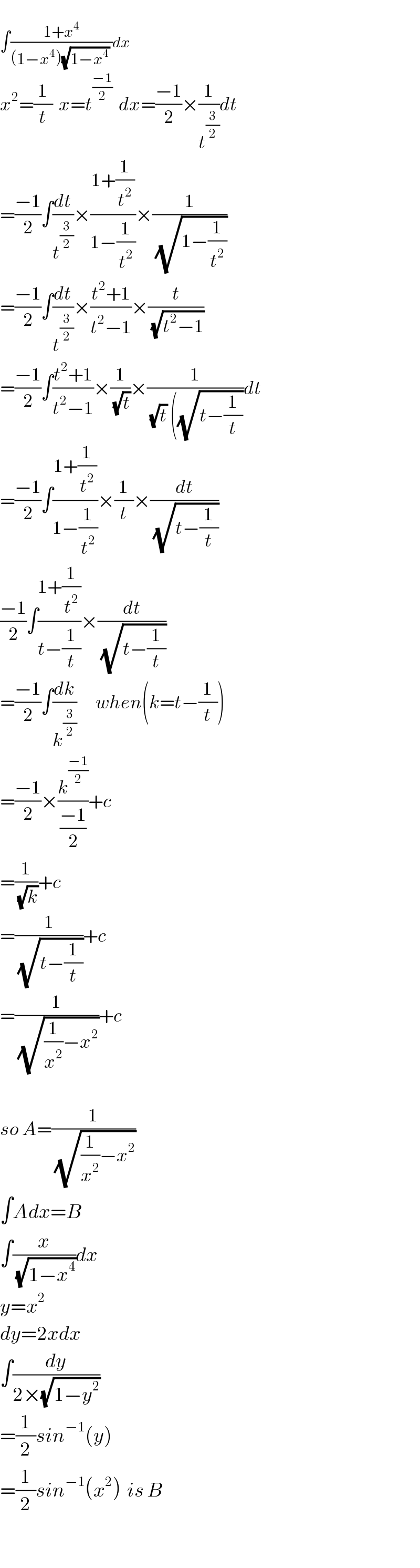
| ||
Question and Answers Forum | ||
Question Number 36801 by rahul 19 last updated on 05/Jun/18 | ||
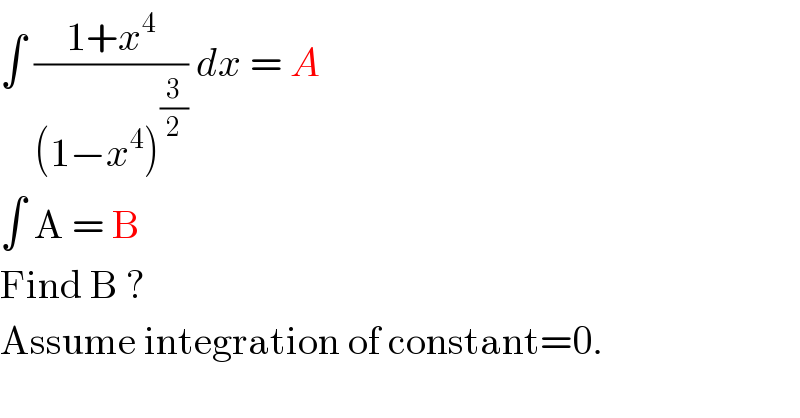 | ||
Answered by MJS last updated on 05/Jun/18 | ||
![A=(x/(√(1−x^4 ))) B=(1/2)arcsin x^2 A: ∫((1+x^4 )/((1−x^4 )^(3/2) ))dx looks like it′s ((p(x))/(√(1−x^4 ))) with p(x) is a polynome let′s try (d/dx)(((p(x))/(√(1−x^4 ))))=(d/dx)(p(x)(1−x^4 )^(−(1/2)) )= =p′(x)(1−x^4 )^(−(1/2)) +p(x)(2x^3 (1−x^4 )^(−(3/2)) )= =((p′(x)(1−x^4 )+2p(x)x^3 )/((1−x^4 )^(3/2) )) ⇒ p′(x)(1−x^4 )+2p(x)x^3 =1+x^4 let′s try p(x)=ax+b; p′(x)=a a+2bx^3 +ax^4 =1+x^4 a=1; b=0 p(x)=x ∫((1+x^4 )/((1−x^4 )^(3/2) ))dx=(x/(√(1−x^4 ))) B: ∫(x/(√(1−x^4 )))dx= [t=x^2 → dx=(dt/(2x))] =(1/2)∫(dt/(√(1−t^2 )))=(1/2)arcsin t= =(1/2)arcsin x^2](Q36810.png) | ||
| ||
Answered by tanmay.chaudhury50@gmail.com last updated on 06/Jun/18 | ||
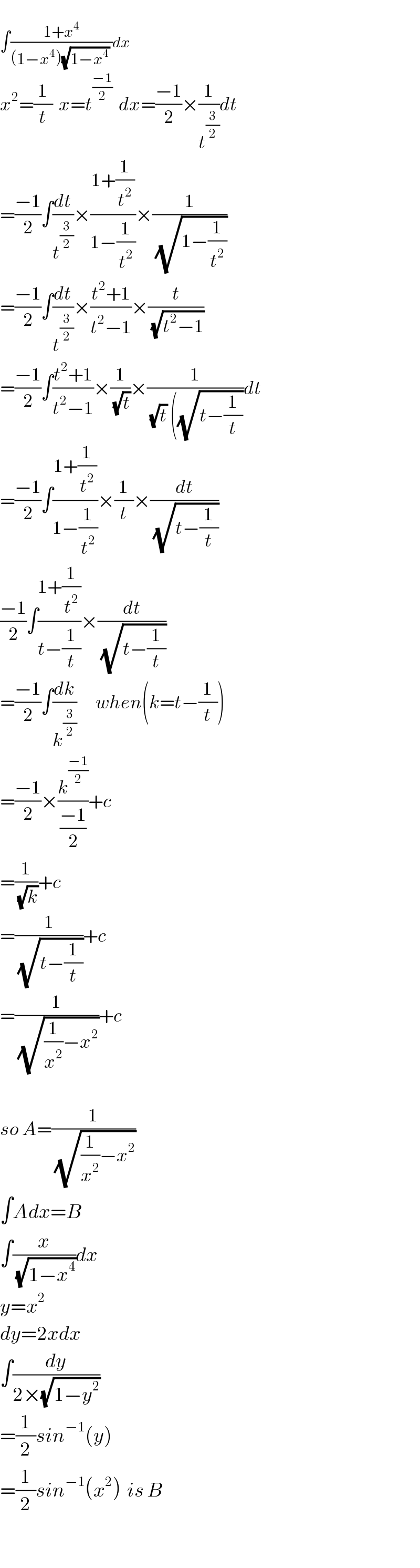 | ||
| ||