
Question and Answers Forum
Question Number 36811 by rahul 19 last updated on 05/Jun/18
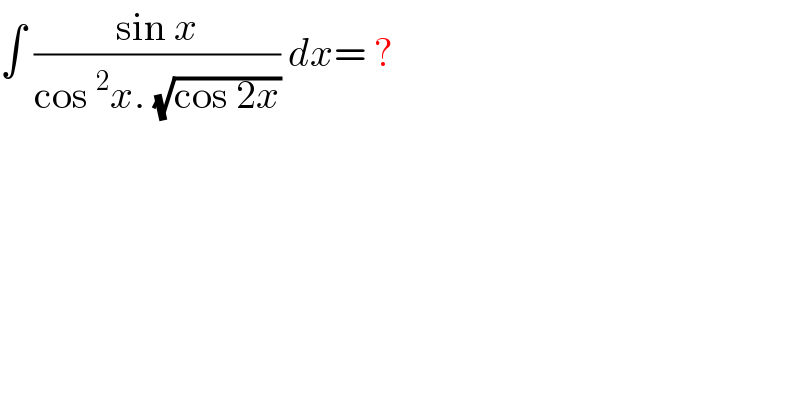
Answered by MJS last updated on 05/Jun/18
![∫((sin x)/(cos^2 x (√(cos 2x))))dx=∫((sin x)/(cos^2 x (√(cos^2 x −sin^2 x))))dx= =∫(((tan x)/(sec x))/((1/(sec^2 x))(√((1/(sec^2 x))−((tan^2 x)/(sec^2 x))))))dx= =∫((sec^2 x tan x)/(√(1−tan^2 x)))dx= [t=tan x → dx=(dt/(sec^2 x))] =∫(t/(√(1−t^2 )))dt= [u=1−t^2 → dt=−(du/(2t))] =−(1/2)∫(du/(√u))=−(√u)=−(√(1−t^2 ))=−(√(1−tan^2 x))+C](Q36813.png)
| ||
Question and Answers Forum | ||
Question Number 36811 by rahul 19 last updated on 05/Jun/18 | ||
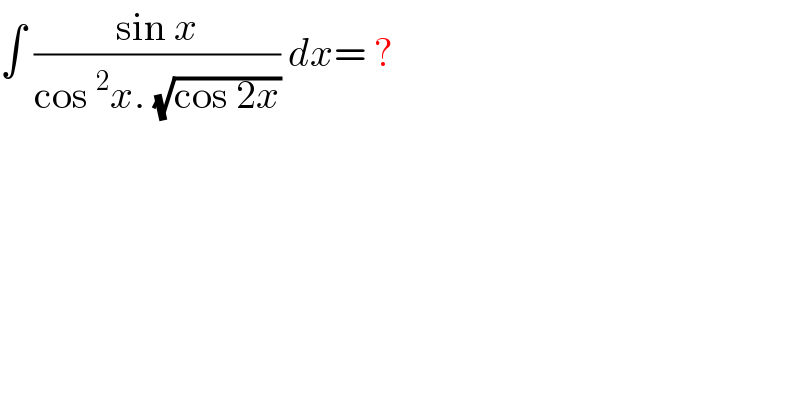 | ||
Answered by MJS last updated on 05/Jun/18 | ||
![∫((sin x)/(cos^2 x (√(cos 2x))))dx=∫((sin x)/(cos^2 x (√(cos^2 x −sin^2 x))))dx= =∫(((tan x)/(sec x))/((1/(sec^2 x))(√((1/(sec^2 x))−((tan^2 x)/(sec^2 x))))))dx= =∫((sec^2 x tan x)/(√(1−tan^2 x)))dx= [t=tan x → dx=(dt/(sec^2 x))] =∫(t/(√(1−t^2 )))dt= [u=1−t^2 → dt=−(du/(2t))] =−(1/2)∫(du/(√u))=−(√u)=−(√(1−t^2 ))=−(√(1−tan^2 x))+C](Q36813.png) | ||
| ||