Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 3682 by Yozzii last updated on 19/Dec/15

Σ_(r=1) ^n (1/(r2^r ))=?

$$\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{r}\mathrm{2}^{{r}} }=? \\ $$

Commented by RasheedSindhi last updated on 19/Dec/15

Σ_(r=1) ^n (1/(r2^r ))=? (1/(1.2^1 ))+(1/(2.2^2 ))+(1/(3.2^3 ))+(1/(4.2^4 ))+...+(1/(n2^n )) (A/r)+(B/2^r )=(1/(r2^r )) A(2^r )+B(r)=1 Let r=0 A(1)=1⇒A=1 B(r)=1−2^r B=((1−2^r )/r) (1/(r2^r ))=(1/r)+(((1−2^r )/r)/2^r ) Σ_(r=1) ^n (1/(r2^r ))=Σ_(r=1) ^n (1/r)+Σ_(r=1) ^n (((1−2^r )/r)/2^r )

$$\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{r}\mathrm{2}^{{r}} }=? \\ $$$$\frac{\mathrm{1}}{\mathrm{1}.\mathrm{2}^{\mathrm{1}} }+\frac{\mathrm{1}}{\mathrm{2}.\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}.\mathrm{2}^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{4}.\mathrm{2}^{\mathrm{4}} }+...+\frac{\mathrm{1}}{{n}\mathrm{2}^{{n}} } \\ $$$$\frac{\mathrm{A}}{{r}}+\frac{{B}}{\mathrm{2}^{{r}} }=\frac{\mathrm{1}}{{r}\mathrm{2}^{{r}} } \\ $$$${A}\left(\mathrm{2}^{{r}} \right)+{B}\left({r}\right)=\mathrm{1} \\ $$$${Let}\:{r}=\mathrm{0} \\ $$$${A}\left(\mathrm{1}\right)=\mathrm{1}\Rightarrow{A}=\mathrm{1} \\ $$$${B}\left({r}\right)=\mathrm{1}−\mathrm{2}^{{r}} \\ $$$${B}=\frac{\mathrm{1}−\mathrm{2}^{{r}} }{{r}} \\ $$$$\frac{\mathrm{1}}{{r}\mathrm{2}^{{r}} }=\frac{\mathrm{1}}{{r}}+\frac{\frac{\mathrm{1}−\mathrm{2}^{{r}} }{{r}}}{\mathrm{2}^{{r}} } \\ $$$$\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{r}\mathrm{2}^{{r}} }=\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{r}}+\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\frac{\mathrm{1}−\mathrm{2}^{{r}} }{{r}}}{\mathrm{2}^{{r}} } \\ $$

Commented by Yozzii last updated on 19/Dec/15

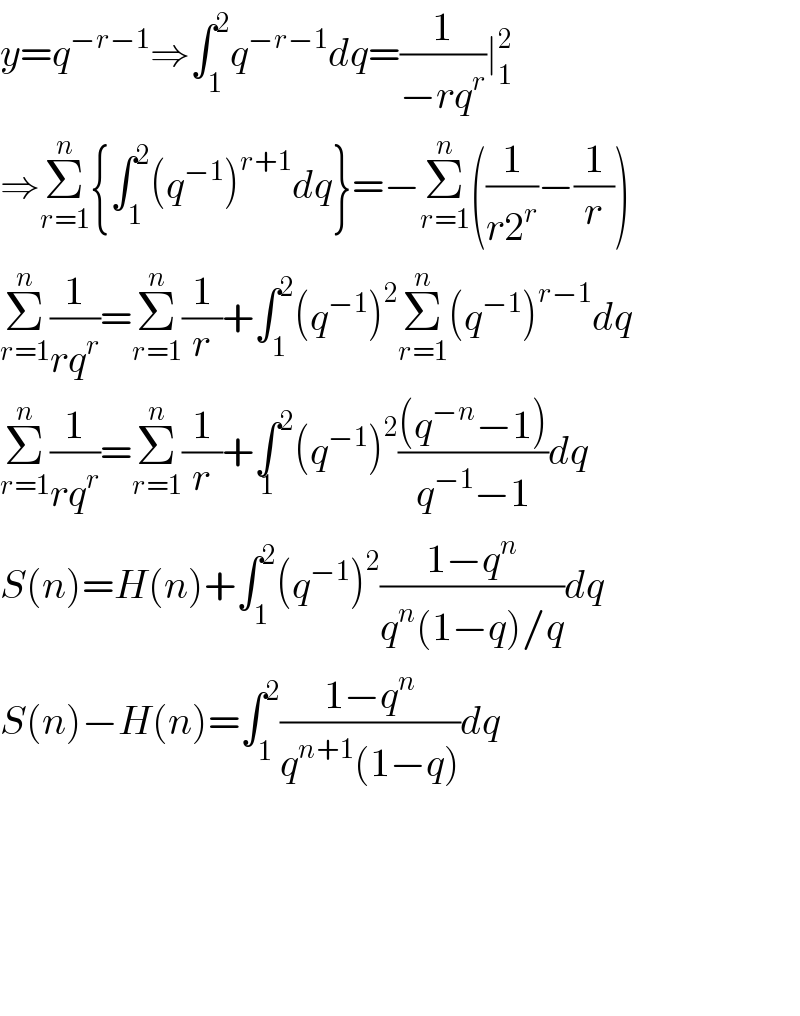
y=q^(−r−1) ⇒∫_1 ^2 q^(−r−1) dq=(1/(−rq^r ))∣_1 ^2 ⇒Σ_(r=1) ^n {∫_1 ^2 (q^(−1) )^(r+1) dq}=−Σ_(r=1) ^n ((1/(r2^r ))−(1/r)) Σ_(r=1) ^n (1/(rq^r ))=Σ_(r=1) ^n (1/r)+∫_1 ^2 (q^(−1) )^2 Σ_(r=1) ^n (q^(−1) )^(r−1) dq^ Σ_(r=1) ^n (1/(rq^r ))=Σ_(r=1) ^n (1/r)+∫^2 _1 (q^(−1) )^2 (((q^(−n) −1))/(q^(−1) −1))dq S(n)=H(n)+∫_1 ^2 (q^(−1) )^2 ((1−q^n )/(q^n (1−q)/q))dq S(n)−H(n)=∫_1 ^2 ((1−q^n )/(q^(n+1) (1−q)))dq

$${y}={q}^{−{r}−\mathrm{1}} \Rightarrow\int_{\mathrm{1}} ^{\mathrm{2}} {q}^{−{r}−\mathrm{1}} {dq}=\frac{\mathrm{1}}{−{rq}^{{r}} }\mid_{\mathrm{1}} ^{\mathrm{2}} \\ $$$$\Rightarrow\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}\left\{\int_{\mathrm{1}} ^{\mathrm{2}} \left({q}^{−\mathrm{1}} \right)^{{r}+\mathrm{1}} {dq}\right\}=−\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\frac{\mathrm{1}}{{r}\mathrm{2}^{{r}} }−\frac{\mathrm{1}}{{r}}\right) \\ $$$$\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{rq}^{{r}} }=\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{r}}+\int_{\mathrm{1}} ^{\mathrm{2}} \left({q}^{−\mathrm{1}} \right)^{\mathrm{2}} \underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}\left({q}^{−\mathrm{1}} \right)^{{r}−\mathrm{1}} {d}\overset{} {{q}} \\ $$$$\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{rq}^{{r}} }=\underset{{r}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{r}}+\underset{\mathrm{1}} {\int}^{\mathrm{2}} \left({q}^{−\mathrm{1}} \right)^{\mathrm{2}} \frac{\left({q}^{−{n}} −\mathrm{1}\right)}{{q}^{−\mathrm{1}} −\mathrm{1}}{dq} \\ $$$${S}\left({n}\right)={H}\left({n}\right)+\int_{\mathrm{1}} ^{\mathrm{2}} \left({q}^{−\mathrm{1}} \right)^{\mathrm{2}} \frac{\mathrm{1}−{q}^{{n}} }{{q}^{{n}} \left(\mathrm{1}−{q}\right)/{q}}{dq} \\ $$$${S}\left({n}\right)−{H}\left({n}\right)=\int_{\mathrm{1}} ^{\mathrm{2}} \frac{\mathrm{1}−{q}^{{n}} }{{q}^{{n}+\mathrm{1}} \left(\mathrm{1}−{q}\right)}{dq} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by Rasheed Soomro last updated on 19/Dec/15

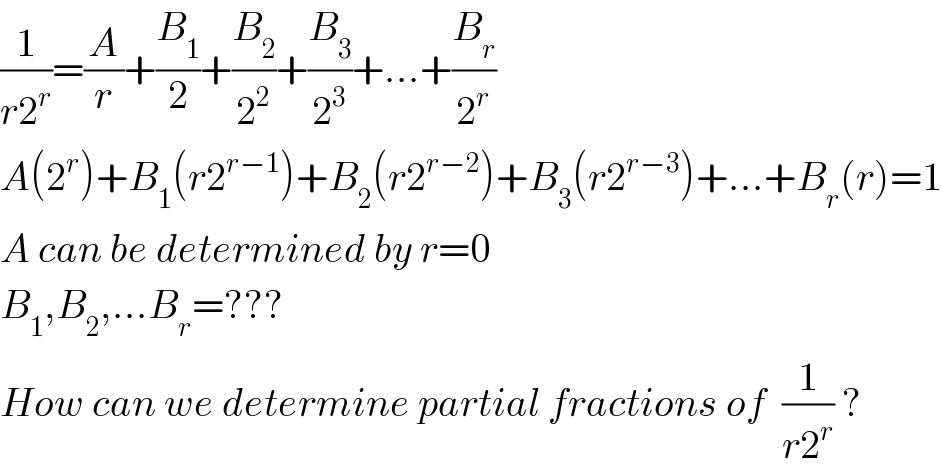
(1/(r2^r ))=(A/r)+(B_1 /2)+(B_2 /2^2 )+(B_3 /2^3 )+...+(B_r /2^r ) A(2^r )+B_1 (r2^(r−1) )+B_2 (r2^(r−2) )+B_3 (r2^(r−3) )+...+B_r (r)=1 A can be determined by r=0 B_1 ,B_2 ,...B_r =??? How can we determine partial fractions of (1/(r2^r )) ?

$$\frac{\mathrm{1}}{{r}\mathrm{2}^{{r}} }=\frac{{A}}{{r}}+\frac{{B}_{\mathrm{1}} }{\mathrm{2}}+\frac{{B}_{\mathrm{2}} }{\mathrm{2}^{\mathrm{2}} }+\frac{{B}_{\mathrm{3}} }{\mathrm{2}^{\mathrm{3}} }+...+\frac{{B}_{{r}} }{\mathrm{2}^{{r}} } \\ $$$${A}\left(\mathrm{2}^{{r}} \right)+{B}_{\mathrm{1}} \left({r}\mathrm{2}^{{r}−\mathrm{1}} \right)+{B}_{\mathrm{2}} \left({r}\mathrm{2}^{{r}−\mathrm{2}} \right)+{B}_{\mathrm{3}} \left({r}\mathrm{2}^{{r}−\mathrm{3}} \right)+...+{B}_{{r}} \left({r}\right)=\mathrm{1} \\ $$$${A}\:{can}\:{be}\:{determined}\:{by}\:{r}=\mathrm{0} \\ $$$${B}_{\mathrm{1}} ,{B}_{\mathrm{2}} ,...{B}_{{r}} =??? \\ $$$${How}\:{can}\:{we}\:{determine}\:{partial}\:{fractions}\:{of}\:\:\frac{\mathrm{1}}{{r}\mathrm{2}^{{r}} }\:? \\ $$

Commented by 123456 last updated on 19/Dec/15

i think it cant be made or the coeficients A,B... doenst be constant

$$\mathrm{i}\:\mathrm{think}\:\mathrm{it}\:\mathrm{cant}\:\mathrm{be}\:\mathrm{made} \\ $$$$\mathrm{or}\:\mathrm{the}\:\mathrm{coeficients}\:\mathrm{A},\mathrm{B}... \\ $$$$\mathrm{doenst}\:\mathrm{be}\:\mathrm{constant} \\ $$

Commented by prakash jain last updated on 19/Dec/15

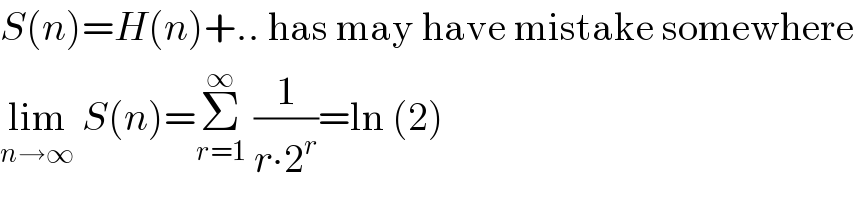
S(n)=H(n)+.. has may have mistake somewhere lim_(n→∞) S(n)=Σ_(r=1) ^∞ (1/(r∙2^r ))=ln (2)

$${S}\left({n}\right)={H}\left({n}\right)+..\:\mathrm{has}\:\mathrm{may}\:\mathrm{have}\:\mathrm{mistake}\:\mathrm{somewhere} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{S}\left({n}\right)=\underset{{r}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{{r}\centerdot\mathrm{2}^{{r}} }=\mathrm{ln}\:\left(\mathrm{2}\right) \\ $$

Commented by prakash jain last updated on 19/Dec/15

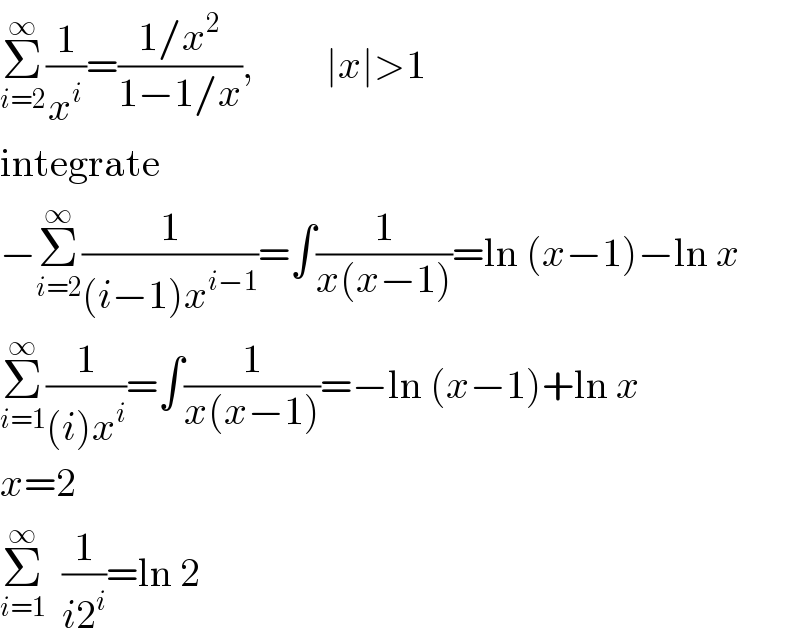
Σ_(i=2) ^∞ (1/x^i )=((1/x^2 )/(1−1/x)), ∣x∣>1 integrate −Σ_(i=2) ^∞ (1/((i−1)x^(i−1) ))=∫(1/(x(x−1)))=ln (x−1)−ln x Σ_(i=1) ^∞ (1/((i)x^i ))=∫(1/(x(x−1)))=−ln (x−1)+ln x x=2 Σ_(i=1) ^∞ (1/(i2^i ))=ln 2

$$\underset{{i}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{x}^{{i}} }=\frac{\mathrm{1}/{x}^{\mathrm{2}} }{\mathrm{1}−\mathrm{1}/{x}},\:\:\:\:\:\:\:\:\:\mid{x}\mid>\mathrm{1} \\ $$$$\mathrm{integrate} \\ $$$$−\underset{{i}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({i}−\mathrm{1}\right){x}^{{i}−\mathrm{1}} }=\int\frac{\mathrm{1}}{{x}\left({x}−\mathrm{1}\right)}=\mathrm{ln}\:\left({x}−\mathrm{1}\right)−\mathrm{ln}\:{x} \\ $$$$\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({i}\right){x}^{{i}} }=\int\frac{\mathrm{1}}{{x}\left({x}−\mathrm{1}\right)}=−\mathrm{ln}\:\left({x}−\mathrm{1}\right)+\mathrm{ln}\:{x} \\ $$$${x}=\mathrm{2} \\ $$$$\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}\:\:\frac{\mathrm{1}}{{i}\mathrm{2}^{{i}} }=\mathrm{ln}\:\mathrm{2} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com